Нормальное рапределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается следующей функцией плотности:

.

Здесь – математическое ожидание, а – среднее квадратичное отклоне­ние нормального распределения.

График дифференциальной функции нормального распределения называется нормальной кривой (кривой Гаусса). Форма кривой зависит от значений а и .

Пaрамeтp а не изменяет форму кривой, a изменяет лишь ее расположение относительно оси У. При а0 кривая сдвинута вправо, а при а0 - влево. С возрастанием  максимальная ордината нормальной кривой убывает.

Пусть нормально распределенная случайная величина Х примет значение, принадлежащее интервалу . Вероятность этого события определяется формулой:

где – функция Лапласа – интегральная функция нормального распределения для случая и, т.е. центрированного и нормированного распределения, .

Вероятность того, что отклонение нормально распределенной величины по абсолютной величине меньше заданного числа  определяется следующим образом:

.

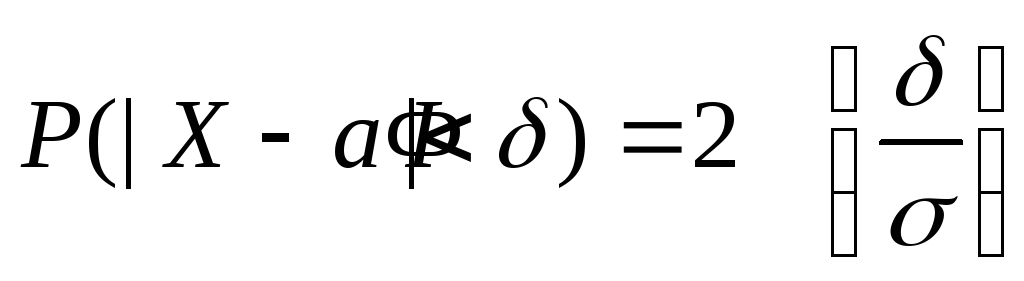Правило трех сигм:.

Используемая литература: [1-5,9,13,15,16,18-21].

Тема 3. Статистические оценки пара­метров распределения

Пусть изучается какой-либо количественный или качественный признак в выборке. При этом значении признакавстречается,–раз и т.д. Наблюдаемые значения признаканазываютсявариантами, а числа –частотами. Последовательность вариант и соответствующих им частот, записанная в возрастающем порядке, называется вариационным рядом. Отношения называются относительными частотами.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значенияотносительную частоту события, т.е.

,

где – число вариант, меньших.

Свойства эмпирической функции распределения совпадают со свойствами функции распределения случайной величины.

Оценки параметров генеральной совокупности

Пусть Х– изучаемый количественный признак генеральной совокупности. Как известно, исчерпывающую информацию о генеральной совокупности дает распределение вероятностей. Естественно, возникает задача оценки (приближенного значения) параметров, которыми определяется это распределение. Например, для нормального распределения таких параметров два – математическое ожидание и среднее квадратическое отклонение.

Как правило, известны лишь выборочные данные из генеральной совокупности, например, значения изучаемого признака х₁,х₂, …,х_n, полученные в результатеnнаблюдений. На их основании и делается вывод относительно всей генеральной совокупности.

Точечные оценки

Точечной называют оценку, которая определяется одним числом. Пусть Θ^* – статистическая оценка неизвестного параметра Θ теоретического распределения. Для того, чтобы оценка была в определенном смысле наилучшей, к ней предъявляется ряд требований:

• Состоятельность. Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки (n) она стремится к истинному значению параметра Θ.

• Несмещенность. Оценка называется несмещенной, если она не содержит систематической ошибки, т.е. среднее значение оценки, определенное по многократно повторенной выборке объема nиз одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра. Другими словами, математическое ожиданиеМ(Θ^*)=Θ.

• Эффективность. Эффективной называют статистическую оценку, которая (при заданном объеме выборки) имеет наименьшую возможную дисперсию D(Θ^*)=D_min.

Доказано, что наилучшей в указанном смысле оценкой математического ожидания М(Х) является , т.е.

В качестве оценки дисперсии признака Хв генеральной совокупностиD(X) берется исправленная выборочная дисперсияD_B^*