
- •Математика:
- •Текст печатается в авторской редакции Содержание
- •Предисловие
- •Методические рекомендации
- •Шкала оценок, правила вычисления рейтинга и возможности его повышения
- •Модульhо-рейтиhговая структура курса "математика”
- •Модульно-рейтинговая структура, график контроля в 1 семестре (корректируется для каждой специальности)
- •Модуль 3. Дифференциальное исчисление функции одной переменной
- •1. Производная функции
- •1.1. Задачи, приводящие к понятию производной
- •1.2. Геометрический смысл производной
- •1.3. Геометрические приложения производной
- •1.4. Связь между дифференцируемостью и непрерывностью. Правила дифференцирования
- •1.5. Таблица производных основных элементарных функций
- •1.6. Производная обратной и сложной функций
- •1.7. Производные высших порядков
- •1.8. Логарифмическое дифференцирование
- •1.9. Дифференцирование неявных функций
- •1.10. Дифференцирование функций, заданных параметрически
- •1.11. Аудиторные задания и задания на повышение рейтинга
- •Свойства дифференциала
- •2.2 Применение дифференциала в приближенных вычислениях
- •2.3. Теоремы о дифференцируемых функциях
- •2.4. Правило Лопиталя
- •2.5. Аудиторные задания и задания на повышение рейтинга
- •3. Исследование поведения функций и построение графиков
- •3.1. Необходимые и достаточные условия возрастания и убывания функции
- •3.2. Признаки существования экстремумов функции
- •Достаточные условия существования экстремума
- •Правило нахождения экстремумов функции
- •3.3. Асимптоты графика функции
- •Правило нахождения точек перегиба функции
- •3.5. Общая схема исследования функций и построения графиков
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •III. Исследование с помощью производной
- •IV. Нахождение дополнительных точек, уточняющих график
- •V. Построение графика функции
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •3.7. Аудиторные задания и задания на повышение рейтинга
- •Найти производную неявно заданной функции
- •3. Написать уравнения касательной и нормали к кривой
- •4. Найти второй дифференциал d2y функции
- •5. Вычислить предел , используя правило Лопиталя
- •6. Исследовать функцию и построить график
- •Решение типового варианта
- •Тестовое задание к модулю 3 "Дифференциальное исчисление функции одной переменной”
- •Образец текущего контроля к модулю 3
- •Теоретические вопросы
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
I. Исследование с помощью элементарной математики
1.
Область
определения
![]()
![]() .
.
2.
Область
изменения функции
![]()
![]() .
.
3.
 и
и
![]() ,
т.е.
функция общего вида.
,
т.е.
функция общего вида.
4. Функция алгебраическая, значит, она непериодическая.
5.
Если
![]() ,
то
,
то![]() ,
значит, график функции пересекает ось
,
значит, график функции пересекает ось![]() в точке
в точке![]() .
Если
.
Если![]() ,
то
,
то![]() ,
значит, график функции пересекает ось
,
значит, график функции пересекает ось![]() в точке
в точке![]() .
.
6.
Для определения интервалов знакопостоянства
отметим на числовой прямой нуль функции,
т.е.
![]() .
Определим знак функции в каждом интервале:
.
Определим знак функции в каждом интервале: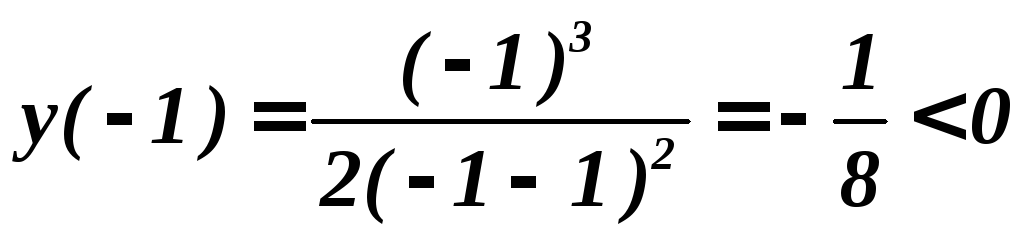 ,
, (см. рис. 8). Следовательно, на интервале
(см. рис. 8). Следовательно, на интервале
![]() график функции расположен ниже оси
график функции расположен ниже оси
![]() ,
а на интервале
,
а на интервале
![]() выше оси
выше оси
![]() .
.

Рис.8
II. Исследование с помощью теории пределов
7.
Так как функция элементарная, то ее
область непрерывности совпадает с
областью определения
![]() .
Исследование на разрыв в точке
.
Исследование на разрыв в точке
![]() и существование вертикальной асимптоты
приведено в примере п. 3.3., т.е. мы
установили, что
и существование вертикальной асимптоты
приведено в примере п. 3.3., т.е. мы
установили, что![]() – вертикальная асимптота.
– вертикальная асимптота.
8.
В том же примере п. 3.3. было установлено,
что горизонтальных асимптот функция
не имеет, а прямая
![]() является правой и левой наклонной
асимптотой.
является правой и левой наклонной
асимптотой.
III. Исследование с помощью производной
9. Интервалы монотонности и точки экстремума найдены в примере п. 3.2.
10. Интервалы выпуклости графика функции и точки перегиба найдены в примере п. 3.4.
IV. Нахождение дополнительных точек, уточняющих график
Для более точного построения можно в каждом из интервалов выбрать дополнительную точку, вычислить в ней значение функции и нанести на рисунок.
V. Построение графика функции

Замечание. Иногда удобно таблицы 1 и 2 совместить в одной таблице.
Пример
2.
Рассмотрим функцию затрат на производство
![]() единицы продукции:
единицы продукции:
![]() .
Средние затраты на выпуск единицы
продукции
.
Средние затраты на выпуск единицы
продукции
![]() .
Построить график функции средних затрат.
Оценить число выпуска единиц продукции,
минимизирующих средние затраты (см. п.
3.3).
.
Построить график функции средних затрат.
Оценить число выпуска единиц продукции,
минимизирующих средние затраты (см. п.
3.3).
Решение.
Исследуем функцию средних затрат
![]() и построим график.
и построим график.
I. Исследование с помощью элементарной математики
1.
Область
определения
![]()
![]() .
.
2.
Область
изменения функции
![]()
![]() .
.
3.![]() .
.
![]() .
Следовательно, функция общего вида.
.
Следовательно, функция общего вида.
4. Функция непериодическая.
5. Не пересекает оси координат.
6.
На интервале
![]() функция положительная, и ее график
расположен выше оси
функция положительная, и ее график
расположен выше оси
![]() .
.
II. Исследование с помощью теории пределов
7.
Функция элементарная, значит, область
непрерывности совпадает с областью
определения
![]() .
Исследуем поведение функции в граничной
точке
.
Исследуем поведение функции в граничной
точке
![]() .
.
![]() .
Отсюда, точка
.
Отсюда, точка
![]() - точка разрыва второго рода и прямая
- точка разрыва второго рода и прямая![]()
![]() вертикальная асимптота.
вертикальная асимптота.
8.
Прямая
![]()
![]() правая наклонная асимптота (см. п. 3.3).
правая наклонная асимптота (см. п. 3.3).
III. Исследование с помощью производной
9.
![]()
![]() критическая точка.
критическая точка.
![]() не существует при
не существует при
![]() .
.
Таблица 3
|
|
0 |
(0,5) |
5 |
| |
|
|
Не сущ. |
|
0 |
+ | |
|
|
Не сущ. |
|
12 |
| |
|
|
|
|
min |
| |
Таким
образом, выпуск 5 единиц продукции
минимизирует функцию средних затрат.
![]()
10.
![]() ,
,
![]() не существует при
не существует при
![]() .
.
Таблица 4
|
|
0 |
|
|
|
не сущ. |
+ |
|
|
не сущ. |
|
IV. Нахождение дополнительных точек, уточняющих график
V. Построение графика функции

3.6. Наибольшие и наименьшие значения функции
Пусть
![]() – непрерывная функция на замкнутом
интервале
– непрерывная функция на замкнутом
интервале
![]() .
Тогда
.
Тогда
![]() достигает свои наибольшие и наименьшие
значения либо на границах интервала,
либо внутри него. Внутри него это могут
быть, очевидно, лишь критические точки.
Отсюда следует правило
нахождения наибольшего и наименьшего
значений непрерывной функции на
сегменте:
достигает свои наибольшие и наименьшие
значения либо на границах интервала,
либо внутри него. Внутри него это могут
быть, очевидно, лишь критические точки.
Отсюда следует правило
нахождения наибольшего и наименьшего
значений непрерывной функции на
сегменте:
Находим производную
 .
.Находим на
 критические
точки функции, в которых
критические
точки функции, в которых
 или не существует.
или не существует.Вычисляем значение функции в критических точках и на концах интервала.
Выбираем из полученных значений функции наибольшее
 и наименьшее
и наименьшее .
.
Пример
1.
Найти наибольшее и наименьшее значение
функции
![]() на отрезке
на отрезке
![]() .
.
Решение.
1.
![]()
2.
![]() т.е.,
т.е.,![]() ,
следовательно,
,
следовательно,![]() – критические точки. Все эти точки
принадлежат
– критические точки. Все эти точки
принадлежат
![]() .
.
3. Вычислим значение функции в критических точках и на концах интервала.
![]() .
.
4.
![]() ,
,![]() .
.
Пример
2.
Требуется изготовить открытый
цилиндрический бак вместимостью
![]() .
Стоимость 1 м2
материала, из которого изготовляется
дно бака, составляет
.
Стоимость 1 м2
материала, из которого изготовляется
дно бака, составляет
![]() руб., а стоимость 1 м2
материала, идущего на стенки бака –
руб., а стоимость 1 м2
материала, идущего на стенки бака –
![]() руб. При каком отношении радиуса дна к
высоте бака затраты на материал будут
минимальными?
руб. При каком отношении радиуса дна к
высоте бака затраты на материал будут
минимальными?
Решение.
Составим
функцию объема, зависящую от радиуса
основания
![]() и высоты бака
и высоты бака![]() :
:![]() .
Тогда
.
Тогда![]() .
Так как площадь основания
.
Так как площадь основания![]() ,
а боковая поверхность
,
а боковая поверхность![]() ,
то общая стоимость затрачиваемого
материала
,
то общая стоимость затрачиваемого
материала![]() .
Выразим функцию
.
Выразим функцию![]() как функцию одной переменной
как функцию одной переменной![]() :
:![]() .
Эта функция является непрерывной для
любого
.
Эта функция является непрерывной для
любого![]() .
Найдем ее критические точки:
.
Найдем ее критические точки:
![]() ;
;
![]() ;
Тогда
;
Тогда![]() и
и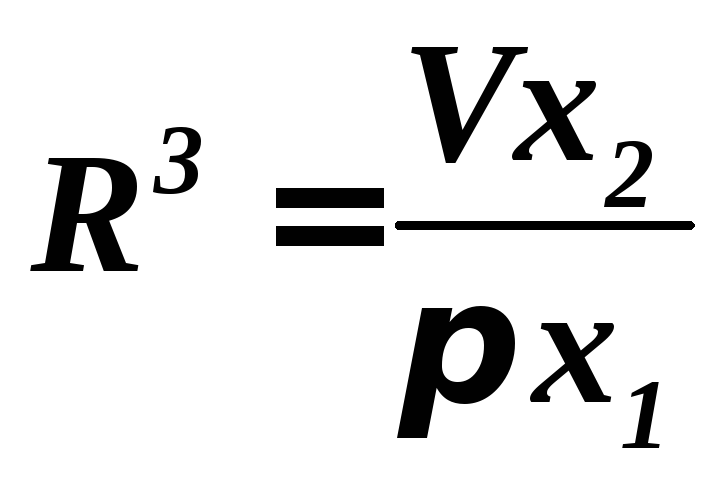 .
.
Таким
образом, искомый радиус
 .
.
Найдем
искомое отношение
 .
.
Замечание. Одним из важнейших приложений дифференциального исчисления является формула Тейлора, которая предлагается для самостоятельного изучения.
