
- •Математика:
- •Текст печатается в авторской редакции Содержание
- •Предисловие
- •Методические рекомендации
- •Шкала оценок, правила вычисления рейтинга и возможности его повышения
- •Модульhо-рейтиhговая структура курса "математика”
- •Модульно-рейтинговая структура, график контроля в 1 семестре (корректируется для каждой специальности)
- •Модуль 3. Дифференциальное исчисление функции одной переменной
- •1. Производная функции
- •1.1. Задачи, приводящие к понятию производной
- •1.2. Геометрический смысл производной
- •1.3. Геометрические приложения производной
- •1.4. Связь между дифференцируемостью и непрерывностью. Правила дифференцирования
- •1.5. Таблица производных основных элементарных функций
- •1.6. Производная обратной и сложной функций
- •1.7. Производные высших порядков
- •1.8. Логарифмическое дифференцирование
- •1.9. Дифференцирование неявных функций
- •1.10. Дифференцирование функций, заданных параметрически
- •1.11. Аудиторные задания и задания на повышение рейтинга
- •Свойства дифференциала
- •2.2 Применение дифференциала в приближенных вычислениях
- •2.3. Теоремы о дифференцируемых функциях
- •2.4. Правило Лопиталя
- •2.5. Аудиторные задания и задания на повышение рейтинга
- •3. Исследование поведения функций и построение графиков
- •3.1. Необходимые и достаточные условия возрастания и убывания функции
- •3.2. Признаки существования экстремумов функции
- •Достаточные условия существования экстремума
- •Правило нахождения экстремумов функции
- •3.3. Асимптоты графика функции
- •Правило нахождения точек перегиба функции
- •3.5. Общая схема исследования функций и построения графиков
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •III. Исследование с помощью производной
- •IV. Нахождение дополнительных точек, уточняющих график
- •V. Построение графика функции
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •3.7. Аудиторные задания и задания на повышение рейтинга
- •Найти производную неявно заданной функции
- •3. Написать уравнения касательной и нормали к кривой
- •4. Найти второй дифференциал d2y функции
- •5. Вычислить предел , используя правило Лопиталя
- •6. Исследовать функцию и построить график
- •Решение типового варианта
- •Тестовое задание к модулю 3 "Дифференциальное исчисление функции одной переменной”
- •Образец текущего контроля к модулю 3
- •Теоретические вопросы
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
Модуль 3. Дифференциальное исчисление функции одной переменной
1. Производная функции
1.1. Задачи, приводящие к понятию производной
1.
Рассмотрим
движение материальной точки по прямой
в одном направлении по закону
![]() ,
где
,
где![]()
![]() время, а
время, а![]()
![]() путь, пройденный за время
путь, пройденный за время![]() .
Отметим некоторый момент времени
.
Отметим некоторый момент времени![]() и обозначим
и обозначим![]() =
=![]() (
(![]() ).
Требуется определить скорость
).
Требуется определить скорость![]() в момент времени
в момент времени![]() .
.
Рассмотрим
другой момент времени
![]() .
Ему соответствует путь
.
Ему соответствует путь![]() .
Тогда за промежуток времени
.
Тогда за промежуток времени![]() точка прошла путь
точка прошла путь![]() .
Очевидно, что средняя скорость движения
за время
.
Очевидно, что средняя скорость движения
за время![]() равна
равна![]() /
/![]() .
Тогда скоростью
.
Тогда скоростью![]() в данный момент времени
в данный момент времени
![]() назовем предел средней скорости при
назовем предел средней скорости при![]() ®0,
т.е.
®0,
т.е.
 .
.
2.
Пусть
дан тонкий прямолинейный неоднородный
стержень длины
![]() .
Определим плотность стержня в любой
точке
.
Определим плотность стержня в любой
точке![]() .
Обозначим через
.
Обозначим через![]() массу отрезка стержня между точками с
координатами 0 и
массу отрезка стержня между точками с
координатами 0 и![]() .
Тогда
.
Тогда![]() - функция от
- функция от![]() ,
т.е.
,
т.е.![]() =
=![]() (
(![]() ).
Фиксируя точку
).
Фиксируя точку![]() и переменную точку
и переменную точку![]() +
+![]() ,
найдем среднюю плотность стержня на
отрезке от точки
,
найдем среднюю плотность стержня на
отрезке от точки![]() до
точки
до
точки
![]() +
+![]() как отношениеD
как отношениеD![]() /
/![]() ,
гдеD
,
гдеD![]()
![]() (
(![]() +
+![]() )
)![]()
![]() .
Плотностью
.
Плотностью![]() стержня в точке
стержня в точке![]() является пределом средней плотности
при
является пределом средней плотности
при![]() ®0,
т.е.
®0,
т.е.
 .
.
Рассмотренные выше и многие другие задачи приводят нас к нахождению пределов одного типа. Абстрагируясь от конкретного содержания задачи, приведем определение.
Определение.
Производной
функции
![]() в точке
в точке![]() называется предел отношения приращения
функции
называется предел отношения приращения
функции![]() в этой точке к вызвавшему его приращению
аргумента
в этой точке к вызвавшему его приращению
аргумента![]() при произвольном стремлении
при произвольном стремлении![]() к нулю.
к нулю.
Для
обозначения производной используют
символы
![]() .
Из определения следует, что
.
Из определения следует, что .
.
Пример.
Пусть
задана функция
![]() и
точка
и
точка
![]() .
Найти
.
Найти![]() .
.
Решение.
![]() .
. ;
;
![]() =6.
=6.
В
задаче о движении точки
![]() ,
т.е. скорость движения материальной
точки, есть производная пути
,
т.е. скорость движения материальной
точки, есть производная пути![]() по времени
по времени![]() ,
а в задаче о плотности стержня
,
а в задаче о плотности стержня![]() .
.
1.2. Геометрический смысл производной
Рассмотрим
график непрерывной функции
![]() и точку
и точку![]() на нем (pис.1). Проведем через точку
на нем (pис.1). Проведем через точку![]() и
некоторую точку
и
некоторую точку
![]() ,
лежащую на графике, секущую.
,
лежащую на графике, секущую.

Рис. 1
Из
свойств прямоугольного треугольника
![]() следует, что угловой коэффициент этой
секущей
следует, что угловой коэффициент этой
секущей![]() ,
где
,
где![]() – угол секущей с осью
– угол секущей с осью![]() .
При
.
При![]() в силу непрерывности функции
в силу непрерывности функции![]() ее приращение
ее приращение![]() .
Поэтому точка
.
Поэтому точка![]() ,
двигаясь по графику, приближается к
точке
,
двигаясь по графику, приближается к
точке![]() ,
а секущая стремится занять свое предельное
положение, называемое касательной
прямой. При этом
,
а секущая стремится занять свое предельное
положение, называемое касательной
прямой. При этом![]() ,
где
,
где![]() – угол образованный касательной с осью
– угол образованный касательной с осью![]() и, значит,
и, значит,![]() .
Откуда следует, что
.
Откуда следует, что![]() .
.
Итак,
значение производной функции
![]() в точке
в точке![]() равно угловому коэффициенту касательной
к графику этой функции в точке с абсциссой
равно угловому коэффициенту касательной
к графику этой функции в точке с абсциссой![]() .
.
В этом заключается геометрический смысл производной.
1.3. Геометрические приложения производной
1.
Зная
геометрический смысл производной, мы
можем записать уравнение
касательной к
графику функций
![]() в точке
в точке![]() :
:
![]() ×
×
2.
Прямая,
проходящая через точку касания
![]() перпендикулярно к касательной называетсянормалью
к
графику функции
перпендикулярно к касательной называетсянормалью
к
графику функции
![]() в этой точке. Ее уравнение, очевидно,
имеет вид:
в этой точке. Ее уравнение, очевидно,
имеет вид:
 .
.
3.
Углом j
между кривыми
![]() и
и
![]() в их общей точке
пересечения
в их общей точке
пересечения
![]() называется угол между касательными к
этим кривым в точке
называется угол между касательными к
этим кривым в точке
![]() и, значит, находится из формулы:
и, значит, находится из формулы:
 .
.
Пример.
В
какой точке
![]() кривой
кривой![]() касательная перпендикулярна к прямой
касательная перпендикулярна к прямой![]() ?
Записать ее уравнение.
?
Записать ее уравнение.
Решение.
![]() .
Угловой коэффициент прямой равен
.
Угловой коэффициент прямой равен![]() .
Значит, угловой коэффициент касательной
равен
.
Значит, угловой коэффициент касательной
равен![]() .
С другой стороны, в точке
.
С другой стороны, в точке![]() он равен
он равен![]() =
=![]() .
Откуда,
.
Откуда,![]() ,
,![]() ,
а уравнение касательной в точке
,
а уравнение касательной в точке![]() имеет вид:
имеет вид:
![]() .
.
1.4. Связь между дифференцируемостью и непрерывностью. Правила дифференцирования
Определение. Процесс нахождения производной называется дифференцированием.
Определение. Функция, имеющая в некоторой точке конечную производную, называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке некоторого интервала, называется дифференцируемой на этом интервале.
Теорема.
Если
функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то она и непрерывна в этой точке.
,
то она и непрерывна в этой точке.
Теорема.
Если
функции
![]() и
и![]() дифференцируемы в точке
дифференцируемы в точке![]() и
и![]() ,
то сумма, разность, произведение и
частное этих функций (последнее, при
условии, что
,
то сумма, разность, произведение и
частное этих функций (последнее, при
условии, что![]() )
также дифференцируемы в этой точке.
При
этом имеют место следующие правила
дифференцирования:
)
также дифференцируемы в этой точке.
При
этом имеют место следующие правила
дифференцирования:
1.
![]() 2.
2.![]() 3.
3.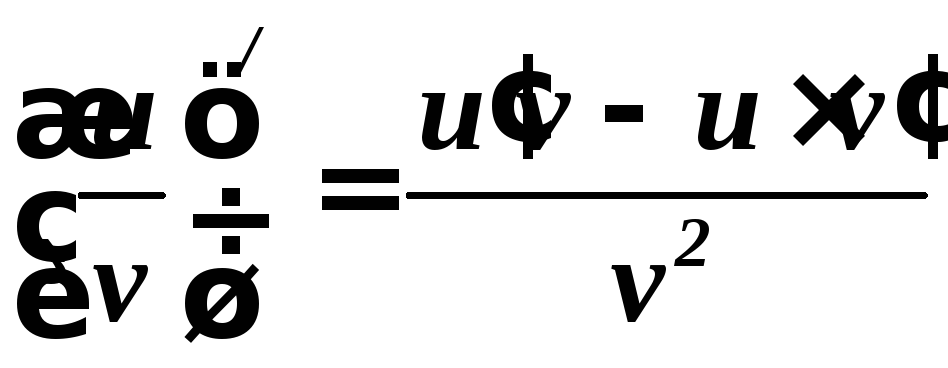
4.
![]() 5.
5. 6.
6.
Теорема.
Производная
постоянной функции равна нулю,
то
есть, если с – постоянная функция, то
![]() .
.
