Достаточные условия существования экстремума

1. (Исследование функции на экстремум по первой производной).

Если непрерывная функция имеет производную во всех точках некоторого интервала, содержащего критическую точку (за исключением, может быть, самой точки ), и если при переходе аргумента слева направо через точку меняет знак с " + " на " ", то функция имеет в этой точке максимум, а при перемене знака с "" на " + "минимум.

2. (Исследование функции на экстремум по второй производной).

Если в критической точке функция дважды дифференцируема и если , то точка есть точка максимума функции , а если , то точка точка минимума.

3. Если в критической точке , а , то функция имеет в точке экстремум, если четное число, а именно: максимум при и минимум при . Если нечетное число, то функция в точке экстремума не имеет.

Правило нахождения экстремумов функции

1. Найти область определения функции.

2. Найти =. Определить критические точки (используя необходимое условие существования экстремума). Для этого нужно решить уравнение = 0 и найти точки, в которых не существует.

3. По одному из достаточных условий (13) определить характер экстремума.

4. Вычислить значения функции в точках экстремума.

Пример 1. Исследовать на существование экстремумов функцию . Определить интервалы монотонности этой функции.

Решение.

1.Функция определена и непрерывна как элементарная функция на множестве .

2. Найдем ее производную:

= 0 тогда и только тогда, когда = 0, откуда = 0 и = 3 являются критическими точками.

Производная не существует при условии , откуда = 1 является также критической точкой.

3. Исследуем характер критических точек по первой производной, вычисляя ее знак слева, и справа от критических точек:

Удобно при нахождении интервалов монотонности и точек экстремума строить таблицу:

Таблица 1

		0	(0,1)	1	(1,3)	3
	+	0	+	не сущ.		0	+
		0		не сущ.		27/8
						min

Критические точки 0; 1; 3 занесены в таблицу в том, порядке, в каком они расположены на числовой оси.

Знаки " + " и " " означают положительность и отрицательность на соответствующем интервале; причем достаточно вычислить знак производной лишь в одной из точек выбранного интервала, так как производная не меняет знак между двумя соседними критическими точками.

Стрелки и означают возрастание и убывание функции на соответствующем интервале.

Итак, функция возрастает на интервалах и , убывает на интервале (1;3).

Проходя через критическую точку = 3, производная меняет знака с " " на " + ", следовательно, функция в этой точке имеет минимум.

4. Значение функции в точке = 3, т.е. .

Пример 2. Исследовать на существование экстремумов функцию . Определить интервалы монотонности этой функции.

Решение.

1. D(y) = .Данная функция является периодической, с периодом , поэтому достаточно исследовать ее на .

2. . Решаем уравнение . Так как при , то – однородное тригонометрическое уравнение. Разделим обе части этого уравнения на . Получим . Следовательно, – критические точки. На отрезке критических точек две: и .

3. Исследуем характер каждой критической точки по второй производной.

Вычислим: Следовательно, в точке функция имеет максимум.

Следовательно, в точке функция имеет минимум.

4. Найдем значение функции в точках максимума и минимума.

.

.

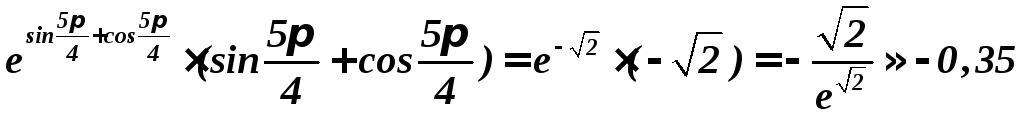Пример 3. Исследовать на существование экстремумов функцию . Определить интервалы монотонности этой функции.

Решение.

1. D(y) =.

2. ; – критическая точка.

3.

Следовательно, согласно третьему достаточному условию существования экстремума заключаем, что в точке функция имеет минимум.

4. .