Глава 6. Дифракция медленных электронов
6.1. Введение
Метод дифракции медленных электронов (ДМЭ) дает информацию о структуре поверхностной кристалличексой решетки. Однако в отличие от микроскопических методов (СЗМ, РЭМ), дифракционные методы не позволяют непосредственно наблюдать атомы поверхности. Во всех методах исследования структуры поверхности, основанных на явлении дифракции, измеряется интенсивность дифрагировавшей волны, в то время как ее фаза остается неизвестной. Для определения положения атомов в ячейке кристаллической решетки необходим расчет, основанный на определенной модели. Поскольку решение такой обратной задачи может быть не единственным, нет полной уверенности в том, что выбранная модель наилучшим образом описывает исследуемый объект. В силу этого развитие сканирующей зондовой микроскопии отодвинуло дифракционные методы исследования поверхности на второй план.
Прежде чем перейти к описанию метода ДМЭ, напомним основные положения кристаллографии поверхности, использующиеся в дифракционных методах.
6.2.Кристаллография поверхности
6.2.1.Трехмерные кристаллические решетки
Объемные периодические структуры (кристаллические решетки твердых тел) описываются в терминах элементарных ячеек (14 решеток Браве), которые определяют трансляционную симметрию кристалла.
Решетка Браве – это бесконечная периодическая структура, образованная дискретными точками и имеющая одинаковый пространственный порядок и ориентацию независимо от того, какую ее точку мы приняли за исходную. Решетка Браве образована всеми
точками с радиусами-векторами |
G |
H |
|
G |
(6.1) |
||
R =αa |
+ βb |
+γc , |
230
где aG, b исG – любые векторы, не принадлежащие одной плоскости, а α, β иγ – целые числа. Вектор R называют вектором транс-
ляции, а векторы aG, b исG – основными векторами решетки Бра-
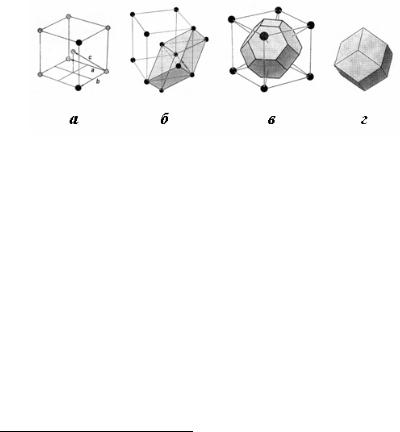
ве. Для примера на рис.6.1, а приведена структура объемноцентрированной кубической (о.ц.к.) решетки Браве.
Примитивная (элементарная) ячейка решетки – это объем пространства, который, будучи подвергнут всем трансляциям, образующим решетку Браве, заполняет все пространство, нигде не пересекаясь и не оставляя промежутков. Ее определение не является однозначным.
Рис.6.1. Структура объемно-центрированной кубичекой (о.ц.к.) решетки Браве с
тройкой основных векторов a , b и c (а); примитивная (темная) и условная кубическая ячейка (б), ячейка Вигнера–Зейтса (в) и первая зона Бриллюэна для о.ц.к. решетки Браве. Объем примитивной ячейки равен половине объема условной кубической ячейки. Ячейка Вигнера–Зейтса представляет собой «усеченный октаэдр», шестиугольные грани которого рассекают пополам отрезки прямых, соединяющих центральную точку с вершинами куба условной о.ц.к. ячейки. Квадратные грани октаэдра рассекают пополам отрезки прямых, соединяющих центральную точку с центральными точками каждой из шести соседних кубических ячеек 78)
Отметим, что элементарная ячейка содержит только одну точку решетки Браве, поэтому объем любой элементарной ячейки независимо от ее определения равен обратной плотности точек в решетке
V0 =1/ n .
Условная элементарная ячейка – область, которая заполняет все пространство без перекрытия, будучи подвергнутой трансляциям, принадлежащим некоторому подмножеству всех трансляций,
78) Н. Ашкрофт, Н. Мермин, Физика твердого тела. – М.: Мир, 1979.
231
образующих решетку Браве. Таким образом, условная ячейка может не совпадать с элементарной и не обязательно содержит одну точку решетки. Обычно условную ячейку выбирают больше элементарной таким образом, чтобы она обладала необходимой симметрией. Так, для о.ц.к. решетки условной ячейкой является кубическая, в то время как элементарная ячейка имеет более сложную структуру (см. рис.6.1, б). В то же время для простой кубической решетки элементарная и условная ячейки совпадают.
Величина, определяющая характерный размер условной ячейки, называется постоянной решетки. Таким образом, постоянная решетки может быть больше, чем минимальное расстояние между атомами в кристаллической решетке.
Ячейка Вигнера–Зейтса – это элементарная ячейка с центром в некоторой точке решетки и занимающая область пространства, лежащую ближе к данной точке, чем к остальным. Для о.ц.к. решетки Браве ячейка Вигнера–Зейтса представляет собой «усеченный октаэдр», вписанный в куб условной ячейки (см. рис.6.1, в).
Для каждой решетки Браве можно построить обратную решетку, образованную множеством точек с радиусами-векторами (век-
торами трансляции обратной решетки) :
gG = haG* + kb* + lcH* , |
(6.2) |
где основные векторы обратной решетки определяются соотношениями :
G |
* |
|
|
2π |
|
|
G |
G |
|
|
a |
|
= |
|
|
|
|
|
b |
×c , |
(6.3) |
|
|
V |
|
|||||||
G |
* |
|
|
2π |
|
|
G |
G |
|
|
b |
|
= |
|
|
|
|
|
c |
×a , |
(6.4) |
|
|
V |
|
|
||||||
K* |
|
2π |
G |
G |
|
|||||
c |
|
= |
|
a ×b |
(6.5) |
|||||
|
V |
|
||||||||
и V = (aG×b) cG. Вектор трансляции обратной решетки имеет раз- exp(igrG) ,
обладающую периодичностью прямой решетки Браве. Из условия периодичности
exp(igrGG) = exp(igG(rG+ R))
следует, что exp(igRG ) =1 и
232
gGR = 2πm , |
(6.6) |
где т – целое число. Тогда из выражений (6.1) и (6.2) получаем
2π(hα + kβ + lγ )= 2πm .
Следовательно, сумма произведений hα + kβ + lγ является целым числом. Поскольку числа α, β иγ могут быть любыми целыми числами, то и h, k иl также являются целыми числами.
Элементарная ячейка Вигнера–Зейтса для обратной решетки называется первой зоной Бриллюэна. В качестве примера на рис.6.1, г показана первая зона Бриллюэна для о.ц.к. решетки Браве.
6.2.2. Двумерные кристаллические решетки
Поверхность представляет собой разрыв трехмерной периодичности кристалла в одном из направлений. По аналогии с трехмерным случаем кристаллическую решетку поверхности характеризу-
ют двумерным вектором трансляции |
|
Rs = αaGs + βbGs , |
(6.7) |
где векторы aGs иbs называются основными векторами поверхно-
стной решетки. Анализ свойств симметрии двумерных систем приводит к пяти различным типам поверхностных решеток Браве:
1) квадратная (с осью вращения четвертого порядка), для которой основные векторы равны по модулю ( as = bs ), а угол между
ними составляетϕ = 90D;
2)прямоугольная ( as ≠ bs ,ϕ = 90D);
3)прямоугольная центрированная ( as ≠ bs ,ϕ = 90D);
4) гексагональная (с осью вращения шестого порядка,
as = bs ,ϕ = 60D);
5)косоугольная ( as ≠ bs ,ϕ ).
Изображения ячеек данных решеток приведено на рис.6.2.
233
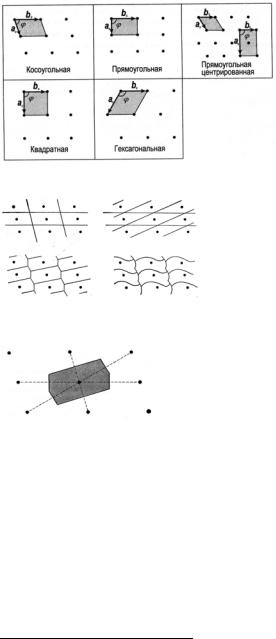
Рис.6.2. Пять типов поверхностных решеток Бра-
ве. Векторы aGs и bs – основные векторы решетки Браве, ϕ – угол между
ними. Элементарные поверхностные ячейки закрашены [5]
Рис.6.3. Некоторые возможные способы выбора примитивной ячейки для двумерной (поверхностной) решетки Браве 79)
Рис.6.4. Ячейка Вигнера–Зейтса для двумерной (поверхностной) решетки Браве. Шесть сторон ячейки рассекают пополам отрезки прямых, соединяющих центральную точку с шестью соседними (эти отрезки показаны пунктиром) 79)
Аналогично случаю трехмерной кристаллической решетки, для двумерной (поверхностной) решетки также можно ввести понятия примитивной или элементарной ячейки, условной элементарной ячейки, ячейки Вигнера–Зейтса и зоны Бриллюэна. В качестве иллюстрации на рис.6.3 показаны четыре варианта выбора примитивной ячейки, а на рис.6.4 – ячейка Вигнера–Зейтса для косоугольной поверхностной решетки Браве.
79) Н. Ашкрофт, Н. Мермин, Физика твердого тела. – М.: Мир, 1979.
234