
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
Если φ= 0, то (2.62) имеет вид
P(0) ≡ |
|
0 0 |
|
+ |
|
1 1 |
|
= I , |
(2.63) |
|
|
|
|
т.е. представляет собой, как это следует из условия полноты (2.6), тождественное преобразование, которое не меняет состояние кубита.
В теории квантовых вычислений важную роль играет так называемое преобразование Адамара (его называют также преобразованием Уолша-Адамара). Матричная и операторная формы этого преобразования имеют вид
H ≡ |
1 |
(σ1 |
+σ3 ) = |
1 |
1 |
1 |
= |
|
|
|
|
|
|||||
2 |
2 |
|||||||
|
|
|
1 |
−1 |
(2.64) |
=12 ( 0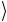 + 1
+ 1 )
)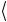 0 +( 0
0 +( 0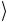 − 1
− 1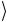 )
)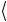 1 .
1 .
Врезультате действия этого преобразования, например, на базисное состояние 0 , представляющее число 0, получаем состояние
, представляющее число 0, получаем состояние
H 0 = 12 (0
= 12 (0 + 1
+ 1 ),
),
которое является однородной суперпозицией “нуля” и “единицы”. Унитарная действительная матрица Н удовлетворяет условию (см. задачу 9 в конце этого раздела):
Н2=1, |
(2.65) |
т.е. совпадает со своей обратной матрицей, а ее собственные значения равны ± 1.
Рассмотрим теперь произвольный однокубитовый гейт. Он описывается некоторой унитарной матрицей 2×2
ˆ |
u |
w |
U = |
. |
|
|
|
|
|
v |
z |
|
81 |
|
Эта матрица содержит 4 комплексных матричных элемента, т.е. 8 действительных величин, на которые накладывается ряд ограничений, вытекающих из условия унитарности (2.54)
ˆ + ˆ |
|
* |
v |
* |
u w |
2 |
+ |
|
2 |
* |
w |
+ |
* |
z |
|
|||
u |
|
|
|
|
|
= |
| u | |
|
| v | |
u |
|
v |
=1. |
|||||
U U = |
|
* |
z |
* |
* |
+vz |
* |
|
2 |
+ |
|
2 |
||||||
|
w |
|
|
v z |
|
uw |
|
| w | |
| z | |
|
||||||||
Отсюда следует, что
| u |2 + | v |2 = | w |2 + | z |2 = 1
(2.66)
uw* + vz* =0.
Эти уравнения представляют собой 4 действительные условия,
накладываемые на элементы матрицы ˆ . Поэтому произвольная
U
унитарная матрица характеризуется четырьмя действительными
параметрами. Если выделить в ˆ некоторый общий фазовый мно-
U
житель, то оставшаяся матрица сводится к оператору конечных вращений (2.48) для спина 1/2.
Переходя к матрицам Паули, получаем
|
|
|
|
|
Φ |
|
ˆ |
= e |
iα |
e |
i |
2 nGσG |
(2.67) |
U |
|
|
. |
Эта матрица зависит, как и говорилось выше, от четырех действительных параметров – фазы α, угла Φ и двух углов θ и φ, опре-
деляющих |
направление |
единичного |
вектора |
nG ={sin θ cos φ, sin θ sinφ, cos θ} . |
Если воспользоваться |
свойст- |
|
вом (2.44) матриц Паули, то произвольную унитарную матрицу (2.67) можно представить (см. задачу 10 в конце этого раздела) в виде
ˆ |
iα |
Φ |
G G |
Φ |
|
U = e |
[cos |
2 |
+ i(nσ) sin |
2 |
] = |
|
|
|
82 |
|
|

|
|
|
Φ |
+ i sin |
Φ |
cos θ |
ie |
−iφ |
sin |
Φ |
sinθ |
|
|
||||||
|
cos |
2 |
2 |
|
|
2 |
|
|
|||||||||||
= e |
i α |
|
|
|
|
|
|
|
|
|
|
|
|
|
. (2.68) |
||||
|
|
|
|
|
|
Φ |
|
|
|
Φ |
|
|
|
Φ |
|
||||
|
|
ie |
i φ |
sin |
sin θ |
cos |
−i sin |
|
|
|
|||||||||
|
|
|
|
2 |
2 |
2 |
cosθ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Унитарную матрицу можно параметризировать и другими способами. Для некоторых конкретных вычислений, которые будут проводиться в разделе 2.5, оказывается удобной такая параметризация, когда вместо углов θ и φ вводятся параметры γ и χ с помощью
следующих соотношений:
sin θ sin |
Φ |
= sin |
γ |
, |
|
|
|
|||
2 |
2 |
|
(2.69) |
|||||||
|
|
|
|
|
|
|||||
|
Φ |
+i cos θsin Φ |
|
|||||||
cos |
= eiχ cos |
γ |
. |
|||||||
2 |
2 |
|||||||||
|
|
|
|
|
2 |
|
|
|||
Тогда унитарная матрица (2.68) принимает следующий вид:
ˆ = iα
U e
eiχ cos γ
2−eiψ sin 2γ
e−iψ sin |
γ |
|
|
||
2 |
|
||||
|
|
|
, |
(2.70) |
|
|
|
|
γ |
||
e |
−iχ |
cos |
|
|
|
|
|
|
|
||
|
2 |
|
|||
|
|
|
|
|
|
где ψ = φ− π2 . Как и должно быть, эта матрица зависит от четырех
параметров. Помимо общей фазы α, есть две разные фазы χ и ψ,
которые входят в диагональные и недиагональные матричные элементы. Можно показать (см. задачу 11 в конце этого раздела), что параметры χ , ψ и γ связаны с преобразованиями поворотов во-
круг осей y и z.
83
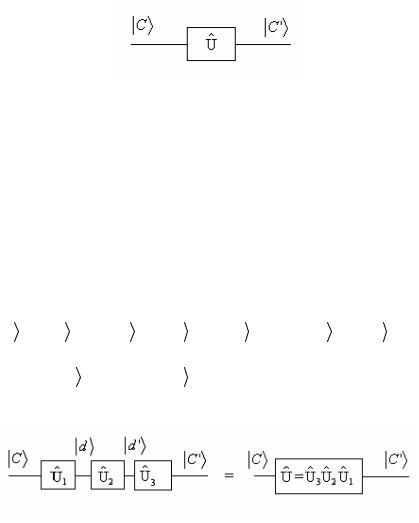
Произвольный однокубитовый гейт ˆ , преобразующий вход-
U
ное состояние кубита 
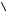 в состояние
в состояние 
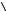 = ˆ
= ˆ 
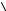 на выходе, изо-
на выходе, изо-
C C' U C
бражается в виде квантовой схемы, показанной на рис. 2.5.
Рис. 2.5
Ради удобства для гейта NOT мы сохраним изображение в виде крестика, как это сделано на рис. 2.4.
Так как произведение унитарных операторов представляет собой унитарный оператор (см. задачу 7 в конце этого раздела), то последовательное применение нескольких однокубитовых гейтов эквивалентно некоторому результирующему однокубитовому гейту. На рис. 2.6 это показано как эквивалентность двух квантовых схем с одним и с несколькими однокубитовыми гейтами, если они
удовлетворяют условию, |
|
|
ˆ ˆ |
ˆ |
ˆ |
, и цепочка преобразо- |
|||||||||||||||||
что U =U3 |
U 2 |
U1 |
|||||||||||||||||||||
ваний выглядит так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
C → |
|
d |
ˆ |
|
|
C |
→ |
|
d' |
ˆ |
|
|
d |
|
ˆ |
ˆ |
|
C |
→ |
|
C' = |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= U1 |
|
|
|
= U2 |
|
|
= U2 |
U1 |
|
|
|||||||||||
|
ˆ |
|
|
d' |
ˆ |
ˆ |
ˆ |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= U3 |
|
|
= U3 |
U2 |
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 2.6
84

Подчеркнем, что результирующее преобразование ˆ зависит, во-
U
обще говоря, от порядка, в котором выполняются операции
ˆ |
, |
ˆ |
2 |
,…, так как преобразования поворота в общем случае не |
U1 |
U |
коммутируют друг с другом.
Теперь рассмотрим несколько примеров физической реализации однокубитовых гейтов.
Спин в магнитном поле
Всамом общем виде однокубитовые гейты сводятся фактически
кунитарным преобразованиям поворота (2.70) в двумерном гильбертовом пространстве.
Естественным физическим процессом, который реализует однокубитовые гейты, является вращение спина в постоянном внешнем
магнитном поле H . Дело в том, что частица, обладающая собственным механическим моментом (спином ħs), имеет и собственный магнитный момент, который из соображений симметрии оказывается параллельным или антипараллельным спину. Поэтому для спина 1/2 оператор магнитного момента записывается в виде
Gˆ |
G |
(2.71) |
μ |
= μσ , |
|
где σi — матрицы Паули, а характерная величина |
μ называется |
|
магнитным моментом1. Взаимодействие магнитного момента с магнитным полем описывается гамильтонианом
ˆ |
Gˆ |
G |
G G |
(2.72) |
H = −μH = − μσH = −μHnσ , |
||||
в котором направление постоянного магнитного поля задается еди-
1 Для электрона магнитный момент направлен против спина, а по абсолютной величине равен магнетону Бора μ0 =| e | =/ 2mec = = 0,927 10−20 эрг/гаусс. Магнитный момент тяжелых частиц – нуклонов,
ядер – пропорционален ядерному магнетону, который на три порядка меньше, так как в нем вместо массы электрона стоит масса протона.
85

ничным вектором |
|
n , т.е. H = H n . Тогда временная эволюция |
||||||||||||||||
вектора состояния |
|
ψ(t) спиновой системы подчиняется уравне- |
||||||||||||||||
|
||||||||||||||||||
нию Шрёдингера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
i |
|
∂ |
|
|
ψ(t) |
= − μHnσ |
|
|
ψ(t) . |
(2.73) |
||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∂t |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ(0) |
имеет вид |
||
Решение этого уравнения с начальным условием |
|
|||||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
где Ω = |
2μH |
|
ψ(t) |
= e i 2 tn σ |
|
|
ψ(0) , |
|
|
|
(2.74) |
|||||||
|
|
|
|
|
||||||||||||||
есть |
|
частота прецессии спина |
в |
|
магнитном поле. |
|||||||||||||
|
|
|
||||||||||||||||
Мы видим, что временная эволюция представляет собой преобразование поворота спинора на угол Φ(t) = Ωt вокруг оси n , т.е.
описывается матрицей конечных вращений ˆ Ω (2.68). Варь-
)
n
,
t
(
R
ируя величину и направление магнитного поля, а также продолжительность времени взаимодействия, можно реализовать любые однокубитовые гейты.
Рассмотрим для иллюстрации несколько частных случаев. Если магнитное поле направлено вдоль оси x, то матрица поворота имеет вид
i |
Ω |
tσx |
|
|
|
Ωt |
isin |
Ωt |
|
2 |
ˆ |
|
cos |
2 |
2 |
|
|||
e |
|
|
= |
|
. |
||||
|
≡ R |
|
Ωt |
|
|
||||
|
|
|
|
x |
|
cos |
Ωt |
||
|
|
|
|
|
isin |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||
Если Ωt = π, то
ˆ |
0 |
1 |
|
= iσx . |
|
Rx (π) = i |
1 |
0 |
|
||
|
|
|
|
||
(2.75)
(2.76)
Такая операция с точностью до фазового множителя i представляет
86
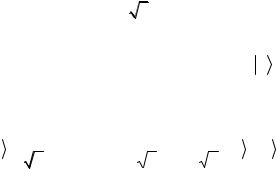
собой, как мы знаем, логический гейт NOT (2.56). Если Ωt = 2π ,
то ˆ π = − , так что происходит только изменение общей фазы
R(2 ) 1
кубита на противоположную.
Если магнитное поле направлено по оси –y, то матрица поворота имеет вид
−i |
Ω |
tσy |
|
|
|
Ωt |
|
|
2 |
|
ˆ |
cos |
2 |
||
e |
|
|
≡ |
|
|||
|
|
Ry (−Ωt) = |
Ωt |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
|
|
|
|
π |
|
|
|
Положив |
Ωt = |
, получим |
|
|
|||
|
|
|
|
2 |
|
|
|
−sin |
Ωt |
|
||
2 |
|
|
||
|
|
|
(2.77) |
|
cos |
Ωt |
. |
||
|
2 |
|
|
|
|
|
|
|
|
ˆ |
π |
|
1 |
1 |
−1 |
|
Ry (− |
2 |
) = |
2 |
|
. |
(2.78) |
|
|
1 |
1 |
|
1
Такая операция действует на базисное состояние 0 = как
0
преобразование Адамара (2.64):
ˆ |
|
π |
|
|
|
1 |
1 |
−1 |
1 |
|
1 |
1 |
|
1 |
( |
|
|
1 ). |
|
|
|
|
|
|
|
|
|
||||||||||||
R |
(− |
|
) |
0 |
= |
|
|
|
|
|
= |
|
|
= |
|
0 |
+ |
||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
2 |
1 |
1 |
0 |
|
|
2 |
1 |
|
2 |
|
|
|
|
Наконец, направив магнитное поле вдоль оси z , получим
i |
Ωtσz |
|
eiΩt / 2 |
|
0 |
|
|
e |
2 |
≡ R (Ωt) = |
|
|
|
. |
|
|
|
ˆ |
|
|
|
−iΩt / 2 |
|
|
|
z |
0 |
e |
|||
|
|
|
|
|
|
||
(2.79)
(2.80)
С помощью такого процесса можно осуществить операцию сдвига относительной фазы (2.62), так как
87
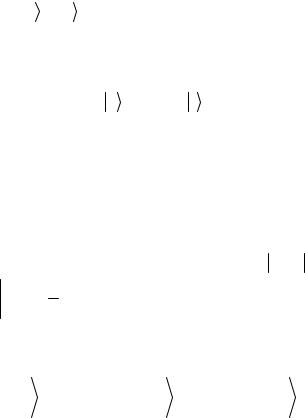
|
|
|
|
|
|
i |
Ωt |
|
|
|
|
|
|
2 |
|
ˆ |
|
|
|
|
e |
||
|
|
||||||
Rz (Ωt) (a |
|
0 |
+ b |
|
1 )= |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
i |
Ωt |
|
|
0 |
|
a |
|
2 |
|
|
|
|
ae |
|
|
|
|||
−i Ωt |
|
|
= |
−i Ωt |
|
= |
|
|
b |
|
|
|
|||
e 2 |
|
|
|
|
2 |
|
|
|
|
be |
|
|
|
||
= ei |
Ωt |
|
2 (a 0 + be−iΩt 1 ). |
(2.81) |
Мы рассмотрели простейший способ манипулирования спиновым кубитом. В более сложной схеме используется постоянное магнитное поле в сочетании с переменным электромагнитным полем. Такая схема применяется, в частности, к ядерным спинам и составляет суть метода ядерного магнитного резонанса (ЯМР).
Направление постоянного магнитного поля H выберем в качестве оси квантования z. Базисные векторы кубита 0 и 1
и 1 , т.е.
, т.е.
состояния Sz = ± 12 , являются собственными состояниями га-
, являются собственными состояниями га-
мильтониана (2.72) взаимодействия магнитного момента с магнитным полем
ˆ |
Sz = ± |
1 |
= − μHσz |
Sz = ± |
1 |
= μH |
Sz = ± |
1 |
|
H |
|
|
|
. (2.82) |
|||||
2 |
2 |
2 |
Следовательно, этим состояниям отвечают два собственных значения энергии
E0,1 = μH . |
(2.83) |
Эти два уровня энергии, описывающие эффект Зеемана, соответствуют тому, что спиновый магнитный момент может быть ориентирован либо по постоянному магнитному полю, либо против него.
88
Расстояние между энергетическими уровнями (2.83) определяет частоту перехода
ω0 = 2 | μ | H . |
(2.84) |
Для типичных значений ядерных магнитных моментов и используемых в экспериментах постоянных магнитных полей ω0 составляет величину порядка 500 МГц, т.е. находится в радиочастотном диапазоне. Два таких энергетических состояния можно эффективно перемешивать с помощью магнитной компоненты переменного электромагнитного поля, частота которого настраивается в резонанс с частотой перехода (2.84). Для электрона в зеемановские сдвиги (2.83) и, следовательно, в частоту перехода (2.84) входит магнетон Бора, который, как уже отмечалось выше, на три порядка больше ядерного магнетона. Поэтому частоты переходов, используемые в экспериментах с электронами, как правило, в несколько раз больше.
Таким образом, рассмотренная схема манипулирования кубитом сводится к взаимодействию двухуровневой квантовой системы с резонансным внешним полем. Поскольку такая модель эффективно работает во многих физических ситуациях, мы остановимся на ней более подробно.
Двухуровневая система в резонансном поле
Помимо рассмотренной выше ситуации с зеемановским расщеплением спиновых магнитных подуровней, есть много других практически важных примеров физической реализации двухуровневой системы, взаимодействующей с резонансным внешним полем. Это могут быть специально выбранные уровни энергии связанных электронных состояний атома или иона. Благодаря богатой структуре спектра связанных состояний, частоты таких двухуровневых атомных систем могут варьироваться в очень широких пределах – от оптического до микроволнового диапазонов. Для иллюстрации многообразия возможностей упомянем, что двухуровневая
89
модель реализуется, например, на колебательных состояниях молекул, или же на квантовых состояниях поступательного движения центра инерции атома или иона в разного типа электромагнитных ловушках. Двухуровневая модель эффективно работает также в задачах квантовой электродинамики резонаторов (КЭР) для описания взаимодействия атома с квантованным электромагнитным полем высокодобротного резонатора.
Все эти системы существенно различаются по масштабам характерных параметров и по физическим механизмам взаимодействия с внешними полями. Тем не менее, структура гамильтонианов, описывающих квантовое поведение этих систем, оказывается одинаковой.
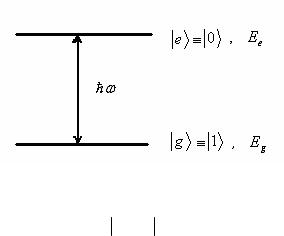
Рассмотрим для определенности изображенную на рис. 2.7 двухуровневую атомную систему, взаимодействующую электродипольным образом с полем электромагнитной волны, частота которой находится в резонансе с частотой выбранного атомного перехода. Заметим, что именно резонансный характер взаимодействия позволяет ограничиться только двумя атомными уровнями и пренебречь остальными состояниями, так как для них условия резонанса не будут выполняться из-за существенно неэквидистантной структуры спектра связанных состояний.
Рис. 2.7
Собственные состояния e и g
и g невозмущенного гамильто-
невозмущенного гамильто-
ˆ “двухуровневого” атома образует полный ортонормирониана H0
ванный базис этой квантовой системы. Им соответствуют два соб-
90
