Классификация кинематических пар

Наименование пары	Класс пары	Подвижность	Схема пары	Условные обозначения
Точечная	1	5
Линейная	2	4
Плоская	3	3

Окончание табл. 2.1

Наименование пары	Класс пары	Подвижность	Схема пары	Условные обозначения
Сферическая	3	3
Цилиндрическая	4	2
Винтовая	5	1
Поступательная	5	1
Вращательная	5	1

Таблица 2.2

Примеры различных видов групп Ассура

Класс	Пор	Вкл	Схема	И	Р	Пример механизма
2	2	1		2	3
		2		2	3

Окончание табл. 2.1

Класс	Пор	Вкл	Схема	И	Р	Пример механизма
		3		2	3
		4		2	3
		5		2	3
3	3 4	1 1		4 6	6 9
4	2	1		4	6

Контрольные вопросы

1. Для чего предназначен механизм?

2. Какая кинематическая цепь является механизмом?

3. Что такое шатун?

4. Что является кинематической парой?

5. Какая кинематическая пара относится к 5-му классу?

6. Какая кинематическая пара относится к 1-му классу?

7. Какая кинематическая пара является плоской?

8. Какая кинематическая пара является низшей?

9. Сколько неподвижных звеньев в 6-звенном механизме?

10. Чему равна степень подвижности группы Ассура?

11. Чему равна степень подвижности группы начальных звеньев, состоящей из стойки и одного подвижного звена?

12. Чем определяется класс группы Ассура?

13. Чем определяется порядок группы Ассура?

14. Чем определяется класс и порядок механизма по классификации Л.В. Ассура?

Полностью материал по данной теме изложен в учебниках [1, с. 38-66], [2, с. 22-43], [3, с. 6-31], [4, с. 7-13], [5, с. 32-66], [6, с. 11-14].

2.2. Лекция №2. Кинематический анализ механизмов

Задачей кинематического анализа является нахождение траекторий, скоростей и ускорений точек звеньев механизма, угловых скоростей и угловых ускорений звеньев механизма. Исходные данные: кинематическая схема механизма (с размерами звеньев) и закон движения начального звена (обычно – кривошипа). Методы кинематического анализа: метод планов, метод кинематических диаграмм, аналитический метод (метод замкнутого векторного контура).

На стадии установившегося движения достаточно произвести кинематический анализ в пределах одного цикла (периода изменения обобщенной координаты начального звена), как правило, это один или два оборота кривошипа. Движение выходных и промежуточных звеньев определяется в два этапа:

1. Устанавливается зависимость кинематических параметров звеньев и точек от обобщенной координаты (функции положения и передаточные функции).

2. Определяется закон изменения обобщенной координаты во времени (после динамического анализа) и, соответственно, кинематические параметры остальных звеньев от времени.

В качестве примера рассмотрим очередность определения кинематических параметров для механизмов с одной степенью свободы (рис. 2.1 и 2.3) при заданной обобщенной координате ₁(t). Для механизма, изображенного на рис. 2.3, искомыми параметрами являются угловые перемещения третьего звена ₃(t), его угловая скорость ₃(t) и угловое ускорение ₃(t). При нахождении углового перемещения ₃(t) на первом этапе определяют функцию положения – это зависимость координаты выходного звена (звена 3) от обобщенной координаты ₃(₁) , а затем угловое перемещение от времени ₃(t).

₃(₁) ₁(t) ₃(t). (2.4)

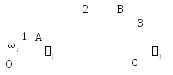
Р и с. 2.3.Четырехшарнирный механизм

Угловая скорость ₃(t) и угловое ускорение ₃(t) соответственно равны:

, (2.5)

где – аналог угловой скорости звена;

U₃₁ = – передаточное отношение.

₃(t) = 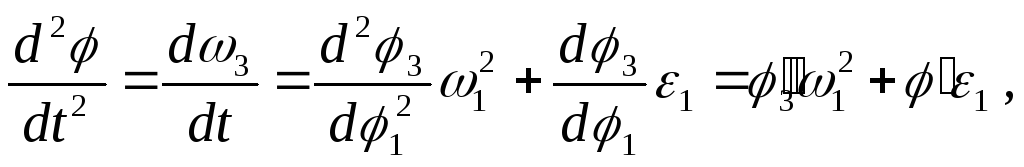(2.6)

где 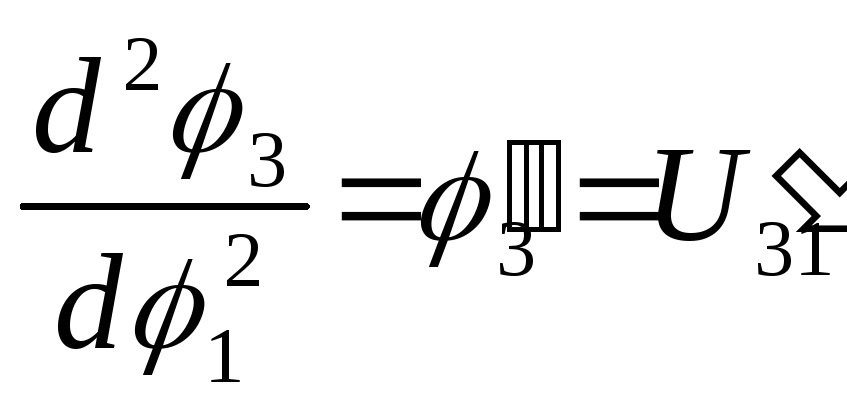– аналог углового ускорения третьего звена;

–угловое ускорение начального звена.

Для механизма, изображенного на рис. 2.1, определению подлежат S₃(t), V₃(t), a₃(t) – перемещение, скорость и ускорение третьего звена.

(2.7)

(2.8)

где – аналог скорости третьего звена.

, (2.9)

где 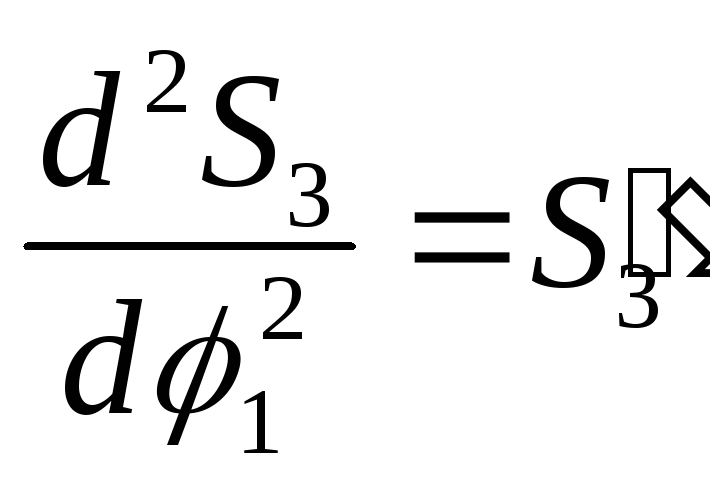– аналог ускорения третьего звена.

В частном случае, при вторые слагаемые выражений (2.6) и (2.9) равны нулю.

Метод планов включает в себя планы механизма, скорости и ускорения. План механизма – это графическое изображение в масштабе взаимного расположения звеньев при заданном значении обобщенной координаты.

Планы скоростей и ускорений – это соответствующие графические изображения в виде пучка векторов абсолютных скоростей или ускорений точек звеньев и отрезков, соединяющих концы векторов, представляющих относительные скорости и ускорения точек в данном положении механизма. Точку, из которой откладываются вектора, называют полюсом. Обычно за полюс принимают стойку. При построении планов используют масштабные коэффициенты, представляющие отношение некоторой физической величины к изображающему ее отрезку на чертеже: _l(м/мм), _V(м/с/мм), _a(м/с²/мм). План механизма строят в 8 или 12 последовательных положениях, начиная с начального звена (в пределах одного периода изменения обобщенной координаты) рис. 2.4.

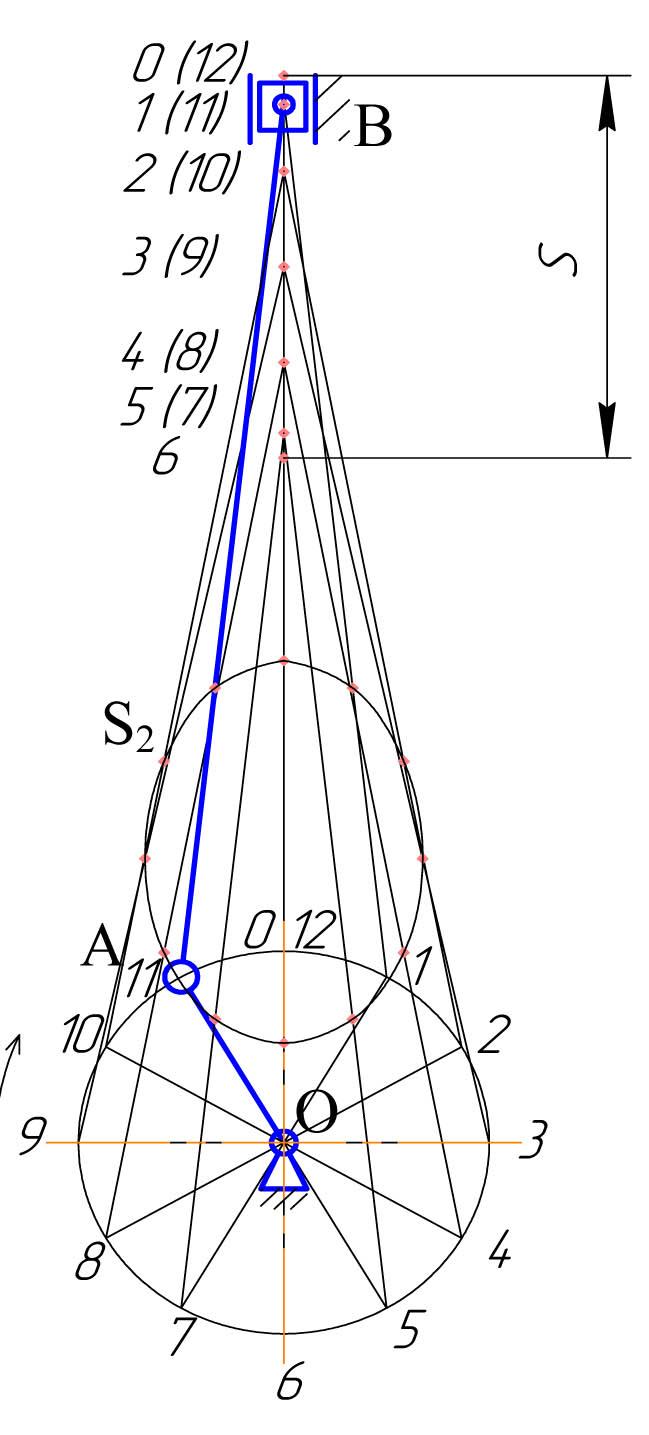
Р и с. 2.4.План кривошипно-ползунного механизма

Положения остальных звеньев находят методом засечек. За нулевое принимают то положение механизма, в котором ведомое (выходное) звено занимает одно из крайних положений ("мертвая точка"). Расчеты при построении планов скоростей и ускорений начинают с нахождения абсолютных скорости и ускорения точки начального звена, угловую скорость которого принимаем постоянной (рис. 2.5):

₁=n/30 (с^-1). (2.10)

Поэтому строящиеся планы представляют собой планы возможных скоростей и ускорений. Их используют для приблизительной оценки скоростей и ускорений. Дальнейшее построение планов производится последовательным наслоением планов групп Ассура. Для этого используется теорема о сложении скоростей и ускорений. Абсолютная скорость точки V_i звена равна векторной сумме переносной V_j и относительной скоростей V_ij. Абсолютное ускорение точки a_i равно векторной сумме переносного a_j и относительного a_ij ускорений, причем последний состоит из двух составляющих: нормальной , направленной по радиусу к центру кривизны траектории, и тангенциальной, направленной перпендикулярно радиусу кривизны

; . (2.11)

Пример (рис. 2.4 (положение 11)):

Дано: ОА, АВ, .

Скорость точки А равна .

Выбираем масштаб плана скоростей (рис. 2.5) и из точкиР, называемой полюсом, откладываем вектор перпендикулярно звенуОА. Этот вектор изображает в выбранном масштабе абсолютную скорость точки А. Далее записываем векторные уравнения для скорости точки В и решаем их графически:

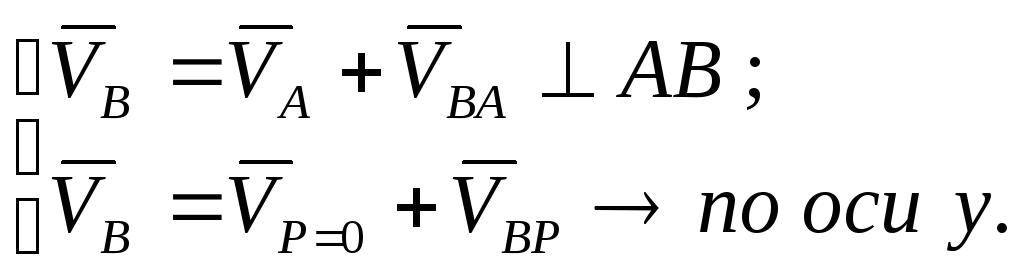(2.12)

Планы скоростей и ускорений обладают изобразительными свойствами, то есть на них получают фигуры, подобные плану механизма, таким образом, находятся V_S2 и а_S2.

Угловая скорость любого звена по модулю равна отношению вектора относительной скорости к плечу:

. (2.13)

Для нахождения направления угловой скорости вектор относительной скорости V_ij мысленно помещают в искомую точку (т. i), принимая известную точку j за неподвижную.

Ускорение точки А равно:

. (2.14)

Выбираем масштаб плана ускорений и откладываем из точкиР вектор параллельно ОА от точки А к центру вращения. Он изображает в выбранном масштабе абсолютное ускорение точки А. Векторные уравнения абсолютного ускорения точки В имеют вид:

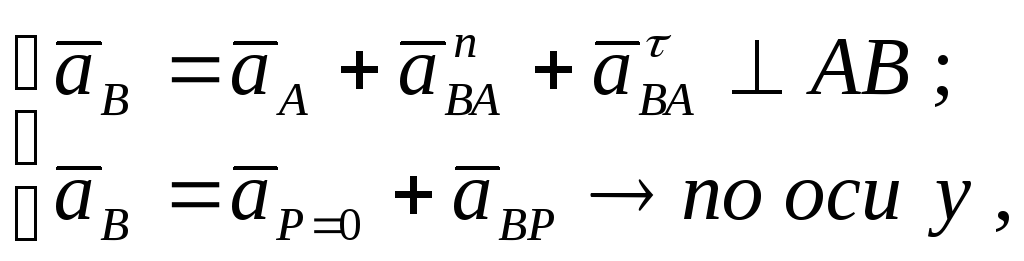(2.15)

где

(мм). (2.16)

Vва

S₂

в

P₀

а P0

в S2 а n

Р и с. 2.5.Планы скоростей и ускорений

и направлен от В к А, – отрезок на плане скоростей.

Планы скоростей и ускорений рассматриваемого механизма изображены на рис. 2.5.

Угловое ускорение звена по модулю равно отношению тангенциальной составляющей относительного ускорения к плечу. Для определения направления вектор тангенциального ускорения помещаем в точкуi, считая точку j за неподвижную

. (2.17)

Метод кинематических диаграмм позволяет графическим способом определять положения отдельных точек звеньев, их скорости и ускорения. Построение начинают с плана механизма. Период изменения обобщенной координаты изображают на оси абсцисс произвольным отрезком L (мм), который разделен на части, пропорциональные углу поворота кривошипа, начиная с начального положения. По оси ординат в масштабе откладываются перемещения интересуемой точки по отношению к ее позиции в начальном положении механизма. Соединяя полученные точки плавной кривой, получим диаграмму перемещения рассматриваемой точки в масштабах

. (2.18)

Построение диаграмм аналога скорости и аналога ускорения производится методом графического дифференцирования, имея в виду, что tg, а . Рассмотрим алгоритм построения графика аналога скорости. Весь графикразбиваем на элементарные участки, заменяя его хордами. На будущем графике аналога скорости выбираем полюсное расстояние Н= (20-50) мм, из которого проводим линии, параллельные хордам. Точки пересечения этих линий с осью ординат являются значениями аналогов скоростейна серединах соответствующих участков в масштабе=,. Аналогично, графически дифференцируя график аналога скорости, получаем график аналога ускоренияв масштабе

, ,

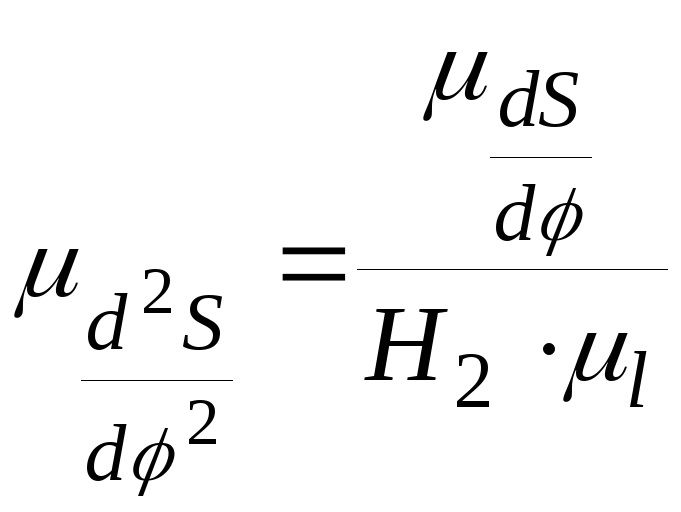где Н₁, H₂ – полюсные расстояния при дифференцировании.

Если ₁ = const, то ось абсцисс является не только осью перемещений, но и одновременно осью времени в масштабе:

, (2.19)

где Т – время одного оборота кривошипа.

(с). (2.20)

При ₁ = const полученные диаграммы являются одновременно диаграммами скорости и ускорения исследуемой точки в масштабах

, ;,. (2.21)

Метод замкнутого векторного контура заключается в том, что звенья механизма изображают в виде векторов, которые образуют на схеме механизма замкнутый контур. Затем составляются векторные уравнения замкнутости каждого контура. Проецируя эти уравнения на оси координат, получают аналитические зависимости положений звеньев от обобщенной координаты (функции положений). За обобщенную координату в дальнейшем принимается угол поворота кривошипа . Дифференцируя по времени или по обобщенной координате уравнения проекций, получают формулы для определения скоростей и ускорений и их аналогов.

Условие замкнутости кинематической цепи механизма, изображенного на рис. 2.6, представляется векторным уравнением

. (2.22)

Из геометрических соображений находим координаты точек А и В, а также тригонометрические функции угла :

; ; (2.23)

; (2.24)

; . (2.25)

Р и с. 2.6. Векторный контур кривошипно-ползунного механизма

Уравнение замкнутости векторного контура (2.22) в проекциях на оси X и Y имеют вид

;

sin+sin=Y_В = e =const. (2.26)

После дифференцирования второго уравнения (2.26) по и преобразований получим

, (2.27)

где – аналог скорости звена 2.

Дифференцирование первого уравнения 2.26 дает

, (2.28)

где и₃₁ – аналог скорости звена 3.

Дифференцируя выражения (2.27) и (2.28) по еще раз, получим

. (2.29)

При этом аналог ускорения звена 2

. (2.30)

Соответственно ускорение точки В равно

, (2.31)

где – аналог ускорения звена 3.

Для определения кинематических характеристик центра масс шатуна т. S₂ рассмотрим векторный контур , при этом, где– проекция на осьХ аналога скорости т. S₂.

, где – проекция на осьY аналога скорости т. S₂ .

; (2.32)

; (2.33)

, (2.34)

где ;

;

.