
- •Введение
- •Понятие, задачи и требования контрольной работы
- •Вопросы выносимые на контроль. Векторы и линейные операции над ними.
- •Демонстрационный вариант контрольной работы.
- •Заключение
- •Список использованной литературы
- •Приложение к курсовой работе.
- •Вариант 1.
- •Вариант 2.
- •Вариант №3.
- •Вариант №4.
- •Вариант№5.
- •Вариант№6.
- •Вариант 7.
- •Вариант№9.
- •Вариант№10.
- •Вариант№11.
- •Вариант№12.
- •Вариант№13.
- •Вариант №14.
- •Вариант№15.
- •Вариант№16.
- •Вариант№17.
- •Вариант№18.
- •Вариант№19.
- •Вариант№20.
- •Вариант№21.
- •Вариант№22.
- •Вариант№23.
- •Вариант24.
- •Вариант№25.
Вопросы выносимые на контроль. Векторы и линейные операции над ними.
Определение. Вектором называется направленный отрезок (рис. 1).
А
– начало, В – конец вектора
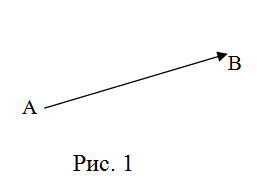
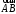 .
.
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение. Вектором называется упорядоченная пара точек.
Определение.
Длина вектора
 – расстояние между его началом и
концом.Определение.
Два вектора называются равными,
если они имеют равные длины и одинаково
направлены. При этом одинаково
направленными называются векторы,
лежащие на параллельных прямых и имеющие
одинаковые направления.
– расстояние между его началом и
концом.Определение.
Два вектора называются равными,
если они имеют равные длины и одинаково
направлены. При этом одинаково
направленными называются векторы,
лежащие на параллельных прямых и имеющие
одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если
начало и конец вектора совпадают, он
называется нулевым:
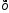 – нулевой вектор: его направление не
определено, а длина
– нулевой вектор: его направление не
определено, а длина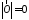 .
.
Определение.
Векторы
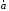 и
и называютсяколлинеарными,
если они лежат на параллельных прямых:
называютсяколлинеарными,
если они лежат на параллельных прямых: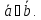
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение. Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
|
а)
Правило параллелограмма (рис.2): начала
|
|
б)
Правило треугольника (рис. 3): начало
|
|
Рис. 2 |
|
Рис. 3 |
в)
Правило сложения нескольких векторов
(рис. 4).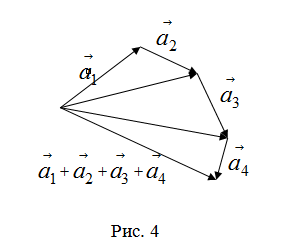
Вектор
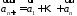 замыкает ломаную линию, построенную
таким образом: конец предыдущего вектора
совмещается с началом последующего и
замыкает ломаную линию, построенную
таким образом: конец предыдущего вектора
совмещается с началом последующего и направлен
от начала
направлен
от начала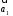 к концу
к концу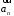 .
.
Умножение на число
Определение.
Произведением вектора
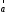 на число
на число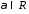 называется
вектор
называется
вектор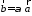 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
а)
 ;
;
б)
 ,
если
,
если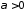 ,
,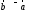 ,
если
,
если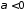 и
и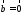 ,
если
,
если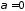 .
.
Произведение
 называется вектором,противоположным
вектору
называется вектором,противоположным
вектору
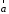 .
Очевидно,
.
Очевидно,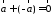 .
.
Определение.
Разностью
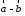 называется сумма вектора
называется сумма вектора и вектора, противоположного
и вектора, противоположного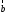 :
: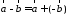 (рис. 5).
(рис. 5).
Начала
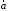 и
и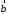 совмещаются в одной точке, и
совмещаются в одной точке, и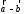 направлен от конца
направлен от конца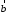 к концу
к концу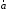 .
.
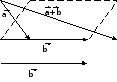
Свойства линейных операций.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
|
Определение.
Результат конечного числа линейных
операций над векторами называется их
линейной
комбинацией: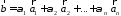 ,
,
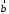 – линейная комбинация векторов
– линейная комбинация векторов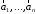 с коэффициентами
с коэффициентами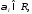
 .
.
Пример.
Пусть
М – точка пересечения медиан треугольника
АВС, а О – произвольная точка пространства.
Представить
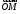 как линейную комбинацию
как линейную комбинацию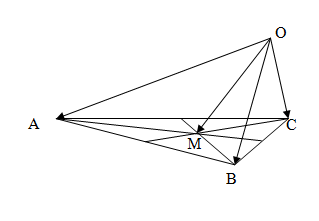
Рис.6
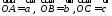 (рис.
6).
(рис.
6).
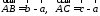 .
Так как точка пересечения медиан
треугольника делит их в отношении 2:1,
считая от вершины, то из правила
параллелограмма следует, что
.
Так как точка пересечения медиан
треугольника делит их в отношении 2:1,
считая от вершины, то из правила
параллелограмма следует, что
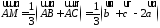 .
.
По
правилу треугольника
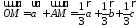 ,
то есть
,
то есть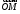 – линейная комбинация
– линейная комбинация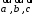 с коэффициентами
с коэффициентами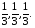
Теорема
1.
Пусть
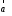 и
и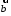 – неколлинеарные векторы. Тогда любой
компланарный с ними вектор
– неколлинеарные векторы. Тогда любой
компланарный с ними вектор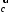 может быть представлен в виде
может быть представлен в виде
 ,
,
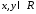 ,
(2.1) где коэффициенты
(2.1) определяются единственным образом.
,
(2.1) где коэффициенты
(2.1) определяются единственным образом.
Представление
вектора
 в виде (2.1) называетсяразложением
его по двум неколлинеарным
векторам.
в виде (2.1) называетсяразложением
его по двум неколлинеарным
векторам.
Теорема
2.
Пусть
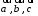 – некомпланарные векторы. Тогда любой
вектор
– некомпланарные векторы. Тогда любой
вектор может быть представлен в виде
может быть представлен в виде
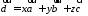 ,
,
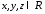 ,
(2.2)причем
единственным образом.
,
(2.2)причем
единственным образом.
Представление
вектора
 в виде (2.2) называетсяразложением
его по трем некомпланарным.
в виде (2.2) называетсяразложением
его по трем некомпланарным.
Проекция вектора на ось.
Координаты вектора.
Определение. Осью называется направленная прямая.
Определение.
Ортом оси
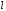 называется единичный вектор
называется единичный вектор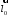 ,
направление которого совпадает с
направлением оси.
,
направление которого совпадает с
направлением оси.
Определение.
Ортогональной проекцией
точки М на ось
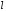 называется основание М1
перпендикуляра, опущенного из М на
называется основание М1
перпендикуляра, опущенного из М на
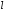 .
.
Определение.
Ортогональной проекцией вектора
 на ось
на ось называетсядлина
отрезка
А1В1
этой оси, заключенного между ортогональными
проекциями его начала и конца, взятая
со знаком «+», если направление вектора
называетсядлина
отрезка
А1В1
этой оси, заключенного между ортогональными
проекциями его начала и конца, взятая
со знаком «+», если направление вектора
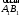 совпадает с направлением оси, и со знаком
«–», если эти направления противоположны
(рис. 8).
совпадает с направлением оси, и со знаком
«–», если эти направления противоположны
(рис. 8).
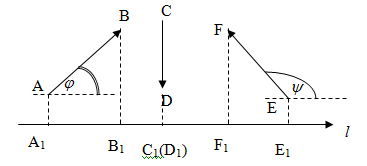
Рис.8
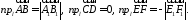
Определение.
Углом между вектором и осью называется
угол, на который нужно повернуть в
положительном направлении ось до
совпадения ее направления с направлением
вектора (положительным считается поворот
против часовой стрелки).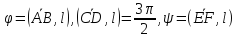 (рис.
8).
(рис.
8).
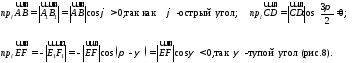
Очевидно, проекцию вектора на ось можно найти по формуле
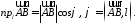
Можно показать, что проекция линейной комбинации векторов равна такой же линейной комбинации их проекций:
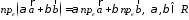 .
.
В частности, проекция суммы векторов равна сумме их проекций:
 .
.
Рассмотрим
прямоугольную декартову систему
координат ХОY.
Обозначим
 – орт оси ОХ,
– орт оси ОХ,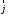 – орт осиOY.
Выберем точку
– орт осиOY.
Выберем точку
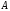 ,
и пусть
,
и пусть – проекции ее на ОХ иOY,то
есть координаты этой точки (рис. 9).
– проекции ее на ОХ иOY,то
есть координаты этой точки (рис. 9).
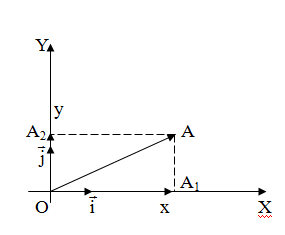
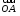 – радиус-вектор
точки
– радиус-вектор
точки
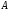 и
и
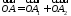 ,
но
,
но
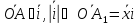 Аналогично
Аналогично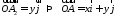 – разложение
– разложение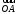 по ортам координатных осей
по ортам координатных осей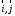 (разложение единственно по теореме
1).
(разложение единственно по теореме
1).
Рис.9
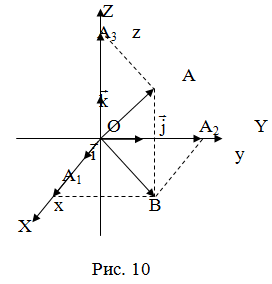
Аналогично
в пространственной системе OXYZ
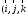 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
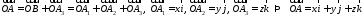 –разложение
–разложение
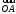 по ортам координатных осей (единственно
по теореме 2).
по ортам координатных осей (единственно
по теореме 2).
Таким
образом, если
задана прямоугольная декартова система
координат (пдск), то со всяким
пространственным вектором
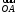 можно связать три числа
можно связать три числа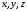 (или два числа
(или два числа ,
если вектор плоский), которые являются
коэффициентами разложения этого вектора
по ортам координатных осей, а также
являются проекциями этого вектора на
координатные оси.
,
если вектор плоский), которые являются
коэффициентами разложения этого вектора
по ортам координатных осей, а также
являются проекциями этого вектора на
координатные оси.
Определение.
Координатами вектора
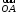 в любойпдск
называются коэффициенты в разложении
этого вектора по ортам координатных
осей.
в любойпдск
называются коэффициенты в разложении
этого вектора по ортам координатных
осей.
Таким образом, можно дать еще одно определение вектора.
Определение. Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример.
Если
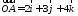 ,
то
,
то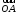 =(2,3,4)
и наоборот, если
=(2,3,4)
и наоборот, если ,
то
,
то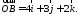
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
 OZ).
OZ).
.
Пусть

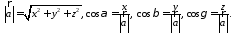
Из этих формул очевидно следует основное свойство направляющих косинусов:

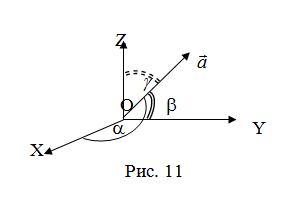
Если
известны длина
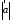 и направляющие косинусы вектора, то
его координаты вычисляются по формулам:
и направляющие косинусы вектора, то
его координаты вычисляются по формулам:
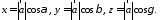
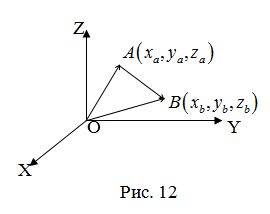
Пусть
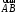 – произвольный вектор в системеOXYZ,
– произвольный вектор в системеOXYZ,
 – радиус-векторы его начала и конца,
– радиус-векторы его начала и конца,
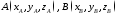 ,
(рис.12).
,
(рис.12).
Тогда:
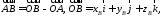
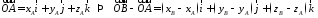 (см.
свойства линейных операций над векторами).
Таким образом,
(см.
свойства линейных операций над векторами).
Таким образом,
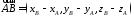 ,
то естьдля
определения
координат вектора надо из координат
его конца вычесть координаты начала.
,
то естьдля
определения
координат вектора надо из координат
его конца вычесть координаты начала.
Определение.
Базисом в пространстве называется любая
упорядоченная тройка некомпланарных
векторов (рис. 13).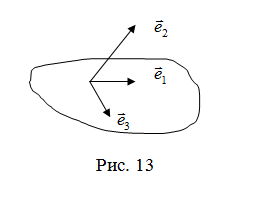
Если
 – базис, то
– базис, то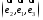 – другой базис, так как изменился порядок
следования векторов.
– другой базис, так как изменился порядок
следования векторов.
Определение. Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой
базис принято обозначать
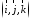 .
.
Из
теоремы 2 следует, что всякий вектор
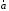 может быть разложен по базису
может быть разложен по базису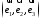 ,
то есть представлен в виде:
,
то есть представлен в виде: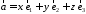 .
Числа
.
Числа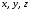 называются координатами
называются координатами в базисе
в базисе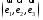 .
.
Определение. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если
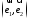 –
базис, то представление вектора в виде
–
базис, то представление вектора в виде
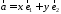 называется разложением
называется разложением по базису
по базису и
и
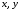 – координаты
– координаты
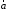 в этом базисе.
в этом базисе.
Определение. Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении.
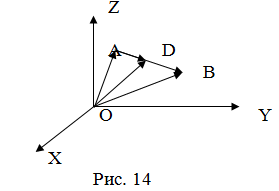
Рассмотрим
задачу: дан отрезок
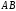 .
Найти точку
.
Найти точку ,
которая делит
,
которая делит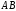 в заданном отношении
в заданном отношении :
: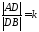 (рис. 14).
(рис. 14).
Введем
прямоугольную декартову систему
координат (пдск)
OXYZ,
тогда
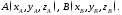
Обозначим
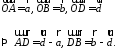
Так
как
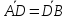 (лежат на одной прямой) и
(лежат на одной прямой) и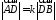 ,
то
,
то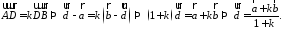 Переходя от этого векторного равенства
к равенству соответствующих координат,
получим:
Переходя от этого векторного равенства
к равенству соответствующих координат,
получим:
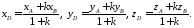 (2.3)
(2.3)
Замечание
1.
Если
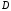 – середина отрезка
– середина отрезка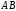 ,
то
,
то ,
поэтому
,
поэтому
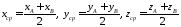 (2.4)
(2.4)
Замечание
1.
Если
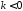 ,
, ,
то точка
,
то точка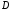 лежит за пределами
лежит за пределами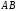 :
так как
:
так как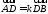 ,
то при
,
то при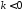

В
этом случае
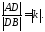
Пусть
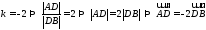 (рис.
15).
(рис.
15).

Скалярное произведение векторов
Определение.
Скалярным произведением векторов
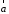 и
и называетсяскаляр
(число),
равный
называетсяскаляр
(число),
равный

Скалярное
произведение обозначается так:
 или
или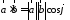 .
.
|
|
Так
как
то
|
Свойства скалярного произведения
1.
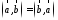 – очевидно из определения.
– очевидно из определения.
2.
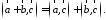
3.
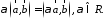
4.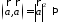
 .
.
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.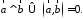
Пример.
Найти, при каком значении
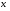 векторы
векторы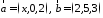 перпендикулярны.
перпендикулярны.
Два
вектора перпендикулярны тогда и только
тогда, когда их скалярное произведение
равно нулю (свойство 5), поэтому найдем
скалярное произведение по формуле
(2.5):
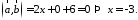
Пример.
Найти угол между биссектрисой
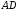 и медианойAM‖ABC,
если
и медианойAM‖ABC,
если
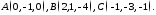
Так
как
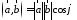 ,
то
,
то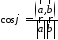 .
(2.6)
.
(2.6)
Найдем
координаты векторов
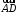 и
и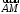 .
Точка
.
Точка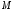 – середина
– середина ,
поэтому по формулам (2.4)
,
поэтому по формулам (2.4)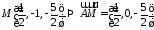 .
.
По
теореме о биссектрисе внутреннего угла
треугольника
 .
Чтобы найти
.
Чтобы найти ,
вычислим длины
,
вычислим длины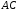 и
и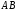 :
:
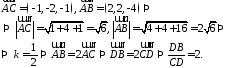
Разделим
отрезок
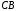 в данном отношении по формулам (2.3):
в данном отношении по формулам (2.3):
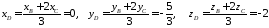 ,
,
отсюда
 .
.
Заметим,
что
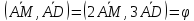 . Это замечание позволит нам не иметь
дело с дробями, так как
. Это замечание позволит нам не иметь
дело с дробями, так как
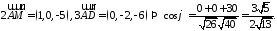
Пример.
Найти
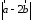 ,
если
,
если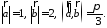
Воспользуемся свойствами 1–4 скалярного произведения:
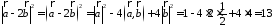 .
.
Отсюда
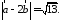
Замечание.
Так как работа силы
 по перемещению материальной точки вдоль
вектора
по перемещению материальной точки вдоль
вектора вычисляется по формуле
вычисляется по формуле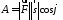 ,
то
,
то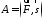 .
.
Векторное произведение векторов
Определение.
Тройка некомпланарных векторов
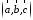 ,
имеющих общее начало, называетсяправой
(левой),
если с конца третьего вектора
,
имеющих общее начало, называетсяправой
(левой),
если с конца третьего вектора
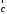 вращение первого вектора
вращение первого вектора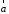 ко второму вектору
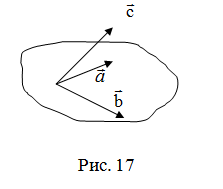
ко второму вектору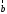 по кратчайшему пути наблюдается против
(по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против
(по) часовой стрелки (рис. 17).
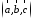 –левая
тройка,
–левая
тройка,
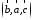 –правая
тройка,
–правая
тройка,
 –левая
тройка.
–левая
тройка.
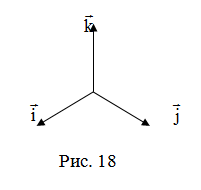
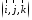 –правая
тройка (рис. 18).
–правая
тройка (рис. 18).
Определение.
Векторным произведением вектора
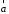 на вектор
на вектор называется вектор
называется вектор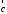 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1.
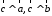 (
(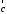 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов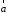 и
и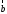 ).
).
2.
Направление
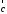 таково, что тройка
таково, что тройка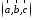 – правая.
– правая.
3.
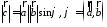 .
.
Векторное
произведение обозначается так:
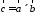 или
или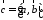 .
.
Замечание. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
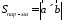 .
.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что

Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
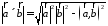 .
(2.7)
.
(2.7)
Пример.
Найти площадь параллелограмма,
построенного на векторах
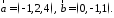
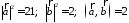 .
.
По
формуле (2.7):
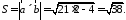
Замечание
2.
Направление вектора
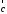 можно также (кроме п.2) определить по
правилу винта: направление вектора
можно также (кроме п.2) определить по
правилу винта: направление вектора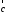 совпадает с направлением поступательного
движения винта в правой резьбой при
вращении его в сторону поворота первого
вектора
совпадает с направлением поступательного
движения винта в правой резьбой при
вращении его в сторону поворота первого
вектора ко второму вектору
ко второму вектору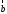 по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).

Свойства векторного произведения.
1.
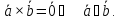
2.
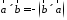 .
.
3.
 – свойство линейности векторного
произведения по первому сомножителю
(без доказательства).
– свойство линейности векторного
произведения по первому сомножителю
(без доказательства).
Векторное произведение также линейно и по второму сомножителю.
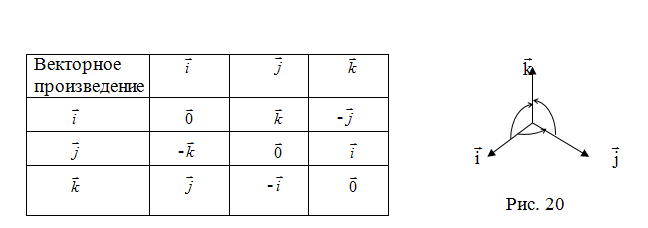
Используя
определение и свойства 1 и 2, составим
таблицу вычисления векторного произведения
базисных векторов
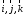 :
векторы, стоящие в левом столбце,
умножаются на соответствующие векторы
верхней строки (рис. 20).
:
векторы, стоящие в левом столбце,
умножаются на соответствующие векторы
верхней строки (рис. 20).
Пусть
в некоторой пдск
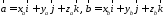 .
Найдем векторное произведение этих
векторов:
.
Найдем векторное произведение этих
векторов:

Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
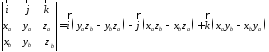 .
.
Таким образом,
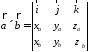 .
(2.8)
.
(2.8)
Пример.
Вычислить векторное произведение
векторов
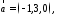
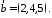
По
формуле (2.8):
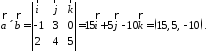
Заметим,
что площадь треугольника, построенного
на векторах
 и
и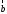 ,
можно вычислить двумя способами: как
половину длины найденного вектора или
используя формулу (2.7). Заметим, что
,
можно вычислить двумя способами: как
половину длины найденного вектора или
используя формулу (2.7). Заметим, что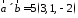 .
.
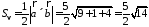
или
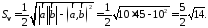
Пример.
Вычислить площадь параллелограмма,
построенного на векторах
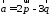 и
и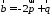 ,
если
,
если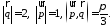
Так
как
 ,
то вычислим векторное произведение,
используя его свойства:
,
то вычислим векторное произведение,
используя его свойства: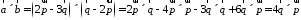 .
.
Отсюда
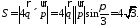
Смешанное произведение векторов
Определение.
Смешанным произведением векторов
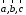 называется число
называется число – скалярное произведение
– скалярное произведение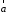 на векторное произведение
на векторное произведение .
.
Смешанное
произведение обозначается так:
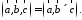
Пусть
в некоторой пдск
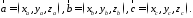
Обозначим
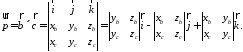
Тогда
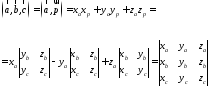
Таким образом,
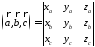 (2.9)
(2.9)
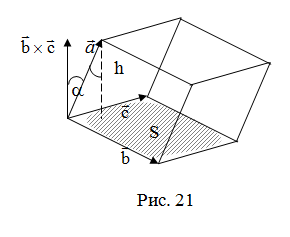
По
определению скалярного произведения
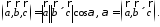
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
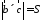 –площадь
параллелограмма,
–площадь
параллелограмма,
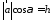 –высота
параллелепипеда,
–высота
параллелепипеда,
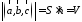 –объем
параллелепипеда.
–объем
параллелепипеда.
Геометрический
смысл смешанного произведения:
модуль
смешанного произведения численно равен
объему параллелепипеда, построенного
на векторах-сомножителях, при этом
 ,
если
,
если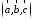 – правая тройка, и
– правая тройка, и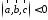 ,
если
,
если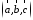 – левая тройка.
– левая тройка.
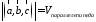 .
.
Свойства смешанного произведения
1.
Необходимым и достаточным условием
компланарности трех векторов является
равенство нулю их смешанного произведения:
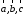 компланарны
компланарны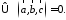
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:

3.
В смешанном произведении векторное и
скалярное произведения можно менять
местами:
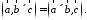
4. Смешанное произведение линейно по каждому из трех сомножителей.
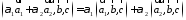 –линейность
по первому сомножителю.
–линейность
по первому сомножителю.
Пример.
Найти объем тетраэдра, построенного на
векторах
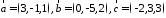 ,
и его высоту, перпендикулярную плоскости
векторов
,
и его высоту, перпендикулярную плоскости
векторов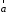 и
и .
.
Объем
тетраэдра в 6 раз меньше объема
параллелепипеда, построенного на этих
векторах, поэтому
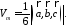
 .
.

Отсюда
 (заметим, что
(заметим, что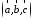 – левая тройка, так как смешанное
произведение отрицательно).
– левая тройка, так как смешанное
произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
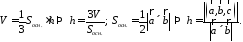
По
формуле (2.7)


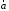 и
и совмещаются в одной точке, и
совмещаются в одной точке, и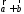 – диагональ параллелограмма,
построенного на
– диагональ параллелограмма,
построенного на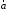 и
и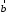 .
.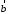 совмещается с концом
совмещается с концом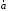 ,
и
,
и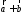 направлен от начала
направлен от начала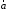 к концу
к концу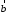 .
.

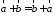
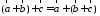
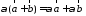
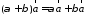
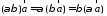
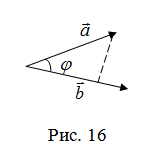
 (рис. 16) или
(рис. 16) или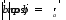 ,
, .
.