
- •Оглавление
- •Часть I. Физические основы электромагнитного 22
- •Часть II. Магнитный контроль 146
- •Часть III. Вихретоковый контроль 281
- •Часть I. Физические основы электромагнитного 6
- •Часть II. Магнитный контроль 96
- •Часть III. Вихретоковый контроль 213
- •От автора
- •Часть I. Физические основы электромагнитного контроля
- •1. Металлы – объекты электромагнитного контроля
- •Плоскость сдвига (с)
- •2. Электрические и магнитные поля в вакууме и веществе
- •2.1. Электрическое поле
- •2.2. Магнитное поле
- •Проводникам
- •2.3. Закон электромагнитной индукции
- •2.4. Система уравнений Максвелла
- •3. Ферромагнетизм
- •3.1. Поведение ферромагнетиков во внешних магнитных полях
- •Намагничивания
- •Коэрцитивной силы по индукции
- •И кобальта от температуры
- •3.2. Энергии ферромагнитного кристалла
- •Намагничивания вдоль кристаллографических осей.
- •3.3. Доменная структура ферромагнетиков
- •3.4. Процессы намагничивания
- •(Скачок Баркгаузена)
- •3.5. Зависимость магнитных свойств ферромагнетика от дефектов структуры
- •Рекордсмены магнитных материалов
- •3.6. Намагничивание магнетиков конечных размеров
- •3.7. Магнитные свойства тела и вещества
- •3.8. Магнитные цепи
- •(Для участка цепи) , (1.130) (для узла цепи) , (1.131)
- •Часть II. Магнитный контроль
- •4. Магнитная дефектоскопия
- •4.1. Граничные условия
- •4.2. Рассеяние магнитного потока дефектом сплошности
- •4.3. Намагничивание изделий
- •Полюсное намагничивание
- •Циркулярное намагничивание
- •Комбинированное намагничивание
- •Намагничивание переменными полями
- •Схемы размагничивания
- •4.4. Расчеты полей дефектов
- •Поля трещины
- •4.5. Mагнитопорошковая дефектоскопия
- •На высоте и
- •4.6. Индукционная дефектоскопия
- •4.7. Феррозондовый метод дефектоскопии
- •4.8. Магнитографическая дефектоскопия
- •Намагниченности ленты от поля (2)
- •4.9. Холловские и другие методы магнитной дефектоскопии
- •4.10. Магнитная толщинометрия
- •5. Магнитный структурно-фазовый анализ металлов и сплавов
- •5.1. Структурная чувствительность физико-механических свойств
- •Структурная чувствительность физико-механических свойств металлов
- •5.2. Контроль механических свойств изделий, упрочняемых холодной пластической деформацией
- •0,07 % От степени холодной пластической деформации
- •Деформированной феррито-перлитной стали с содержанием углерода 0,08 % от температуры отжига
- •5.3. Контроль качества термической обработки стальных изделий
- •От температуры закалки
- •От температуры отпуска
- •5.4. Контроль качества поверхностного упрочнения стальных изделий
- •Коэрцитиметра от относительных значений глубины закаленного слоя
- •5.5. Фазовый магнитный анализ
- •5.6. Устройства магнитного контроля структуры, состава и механических свойств материалов и изделий
- •Индукции деталей с большим коэффициентом размагничивания
- •Часть III. Вихретоковый контроль
- •6. Возбуждение вихревых токов. Скин-эффект.
- •7. Вихретоковый контроль. Вихретоковые преобразователи.
- •8. Сигнал втп. Обобщенный параметр контроля.
- •Сопротивлений витка с переменным током на проводящем полупространстве
- •9. Контроль цилиндрических объектов наружным проходным втп с однородным полем. Выбор наилучших условий контроля.
- •10. Вихретоковый контроль с помощью накладных преобразователей
- •11. Способы ослабления влияния мешающих параметров
- •12. Приборы вихретокового контроля
- •Заключение
- •Список литературы
- •Дополнительная литература
4.4. Расчеты полей дефектов
Точное вычисление
поля дефекта возможно только для ряда
простейших случаев. Аналитически решены
задачи для поля некоторых моделей
дефектов в безграничном пространстве
при
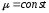 (линейный случай).
(линейный случай).
Поле дефекта
цилиндрической формы
(рис. 2.5). Пусть имеется дефект в виде
цилиндра радиусом
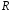 ,
заполненный средой 1 с
,
заполненный средой 1 с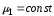 и помещенный в безграничную среду 2 с
и помещенный в безграничную среду 2 с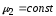 .
Однородное внешнее поле
.
Однородное внешнее поле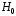 направим вдоль оси
направим вдоль оси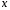 .
Требуется определить суммарное магнитное
поле в средах 1 и 2. Изменение, которое
претерпевает поле
.
Требуется определить суммарное магнитное
поле в средах 1 и 2. Изменение, которое
претерпевает поле вблизи цилиндра, и будет полем
цилиндрического дефекта.
вблизи цилиндра, и будет полем
цилиндрического дефекта.

Рис. 2.5. Цилиндрический дефект Рис. 2.6. Соотношение декартовых
в поле
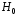 и цилиндрических
координат
и цилиндрических
координат
Задача может быть решена на основе решения уравнений Максвелла (раздел 2.4):
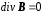 ;
(2.5)
;
(2.5)
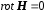 ;
(2.6)
;
(2.6)
c учетом граничных условий (см. раздел 4.1)
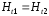 ;
(2.7)
;
(2.7)
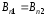 или
или
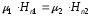 .
(2.8)
.
(2.8)
Выражение
(2.5) означает, что линии вектора магнитной
индукции всегда замкнуты. Выражение
(2.6) указывает на то, что в данном случае
поле можно рассматривать как потенциальное,
поскольку правая часть равна нулю, то
есть отсутствуют сторонние токи, которые
могли бы образовать вихри поля. Потенциальное
поле характеризуется тем, что каждая
его точка имеет магнитный потенциал
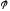 .
Следовательно, можно записать
.
Следовательно, можно записать
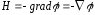 .
(2.9)
.
(2.9)
Это,
впрочем, следует и из (2.5): поскольку
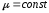 ,
то
,
то
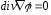 .
(2.10)
.
(2.10)
Последнее уравнение известно как уравнение Лапласа
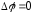 ,
(2.11)
,
(2.11)
где
 -
оператор Лапласа (или лапласиан) - имеет
вид в декартовой системе координат
-
оператор Лапласа (или лапласиан) - имеет
вид в декартовой системе координат
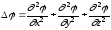 ,
(2.12)
,
(2.12)
в цилиндрической системе координат
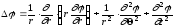 .
(2.13)
.
(2.13)
Теперь
задачу можно сформулировать следующим
образом: найти потенциал
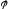 в средах 1 и 2, удовлетворяющий уравнению
Лапласа (2.11) и граничным условиям (2.7) и
(2.8).
в средах 1 и 2, удовлетворяющий уравнению
Лапласа (2.11) и граничным условиям (2.7) и
(2.8).
Будем искать потенциал вне цилиндра в виде:
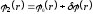 ,
(2.14)
,
(2.14)
где
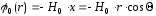 - потенциал исходного поля;
- потенциал исходного поля;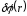 - потенциал дополнительного поля,
обусловленного наличием цилиндра
(потенциал поля дефекта).
- потенциал дополнительного поля,
обусловленного наличием цилиндра
(потенциал поля дефекта).
Определяемое потенциалом (2.14) поле должно обладать следующими свойствами:
1) исчезать на бесконечности;
2)
в силу цилиндрической симметрии зависеть
только от
 и
и
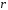 ;
;
3) удовлетворять уравнению Лапласа.
Этим условиям удовлетворяет функция
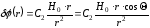 ,
(2.15)
,
(2.15)
в чём можно убедиться непосредственно подстановкой (2.15) в (2.11). Можно также доказать2, что это решение является единственным.
Следовательно, потенциал поля вне цилиндра надо искать в виде
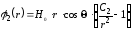 .
(2.16)
.
(2.16)
Внутри цилиндра потенциал поля должен удовлетворять следующим условиям:
1)
не должен обращаться в бесконечность
при
 ;
;
2)
зависеть только от
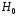 и
и
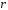 ;
;
3) удовлетворять уравнению Лапласа.
Функцией, удовлетворяющей этим условиям, является
 .
(2.17)
.
(2.17)
Остаётся
определить константы
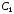 и
и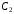 .
Они находятся из граничных условий
(2.7) и (2.8). В цилиндрических координатах
.
Они находятся из граничных условий
(2.7) и (2.8). В цилиндрических координатах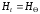 ;
;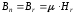 .
.
 ,
(2.18)
,
(2.18)
 ,
(2.19)
,
(2.19)
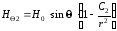 ,
(2.20)
,
(2.20)
 .
(2.21)
.
(2.21)
Из (2.7) и (2.8) с учётом (2.18) . . . (2.21) находим
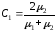 ,
(2.22)
,
(2.22)
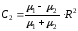 .
(2.23)
.
(2.23)
Таким образом,
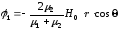 ,
(2.24)
,
(2.24)
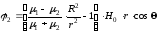 .
(2.25)
.
(2.25)
Следовательно,
 ,
(2.26)
,
(2.26)
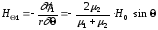 ,
(2.27)
,
(2.27)
 ,
(2.28)
,
(2.28)
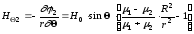 .
(2.29)
.
(2.29)
Перейдём к декартовым координатам. Из рис. 2.6 видно, что
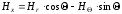 ,
,
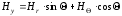 ,
,
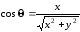 ;
;
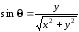 ;
;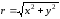 .
.
С учётом этого
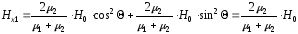 .
(2.30)
.
(2.30)
Аналогично
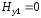 ,
(2.31)
,
(2.31)
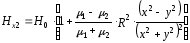 ,
(2.32)
,
(2.32)
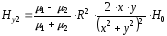 .
(2.33)
.
(2.33)
Основные
характеристики поля цилиндрического
дефекта.
Из (2.32) и
(2.33) видно, что поле цилиндрического
дефекта в среде
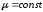 и однородном поле
и однородном поле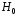 по своей
структуре совпадает с полем дипольной
нити, расположенной в центре дефекта и
имеющей дипольный момент
по своей
структуре совпадает с полем дипольной
нити, расположенной в центре дефекта и
имеющей дипольный момент
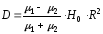 .
(2.34)
.
(2.34)
Из этого главного вывода следует несколько выводов очевидных:
-
топография поля цилиндрического дефекта
не зависит от величины его радиуса
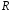 (величина
(величина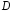 - пропорциональна
- пропорциональна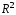 );
);
-
составляющая
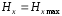 при
при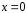 и
и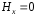 при
при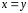 ;
;
-
составляющая
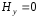 при
при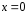 и
и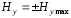 при
при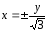 .
.
Поле трещины.Наиболее часто встречающийся поверхностный дефект - трещина с выходом на поверхность. Формы трещин обычно достаточно сложные, но для расчётов их можно упростить и свести к трём модификациям (рис. 2.7). Но даже и для таких форм расчёты не могут быть выполнены точно в связи со сложностью граничных условий.
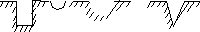
а б в
Рис. 2.7. Простейшие модели поверхностных дефектов
Для расчёта полей поверхностных дефектов используют искусственные приёмы, один из них заключается в следующем.
Грани дефекта (рис. 2.7а) можно рассматривать как торцы намагниченного изделия, на которых образуются магнитные полюса. Магнитный полюс можно описать системой магнитных объёмных и поверхностных зарядов, распределённых с некоторыми плотностями v и s, зависящими от координат.
Если известно
распределение зарядов, то можно определить
поле, которое они образуют в пространстве
(собственно это и будет поле дефекта).
Например, точечный магнитный заряд
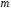 создаёт поле
создаёт поле
 ,
(2.35)
,
(2.35)
 ,
(2.36)
,
(2.36)
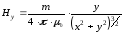 ,
(2.37)
,
(2.37)
 где
где
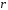 -
расстояние
от точки наблюдения до заряда;
-
расстояние
от точки наблюдения до заряда;
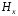 и
и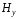 - составляющие поля заряда вдоль координат
- составляющие поля заряда вдоль координат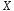 ,
,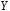 (заряд
помещён в центре при
(заряд
помещён в центре при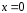 ,
,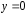 ).
).
Рис. 2.8. Полюса на гранях Рис. 2.9. К расчёту поля трещины
Поле трещины,
изображённой на рис. 2.8 и 2.9, можно
рассматривать в
в простейшем случае как поле от двух
систем зарядов, распределённых по её
граням с плотностью
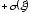 и
и .
.
Элементарный заряд
на единицу длины (в плоскости,
перпендикулярной рисунку 2.9, дефект
бесконечен)
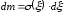 .
Выражение для напряжённости поля в
точке A,
создаваемого элементарным зарядом
.
Выражение для напряжённости поля в
точке A,
создаваемого элементарным зарядом
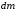 ,
по (2.35):
,
по (2.35):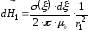 .
Принимая во внимание, что
.
Принимая во внимание, что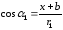 ;
;
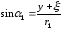 ;
;
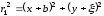 ,
получим в
координатном представлении
,
получим в
координатном представлении
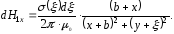
Аналогично можно
записать выражения для
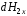 ,
,
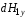 ,
,
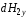 и после
интегрирования по
и после
интегрирования по
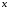 при условии
при условии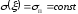 получим
следующие выражения для
получим
следующие выражения для
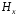 и
и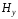 :
:
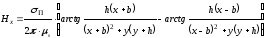 ,
(2.38)
,
(2.38)
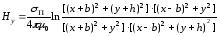 .
(2.39)
.
(2.39)
Графическое представление зависимостей (2.38) и (2.39) дано на рис. 2.10 и 2.11.
Составляющая
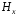 имеет экстремум при
имеет экстремум при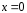 .
Если
.
Если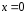 и
и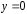 ,
то
,
то
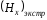 =
=
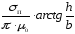 .
(2.40)
.
(2.40)
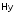
Hy





Hx


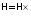














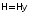
Рис. 2.10. Составляющие Рис. 2.11. Поле рассеяния трещины
