Поля трещины

Если 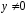, то

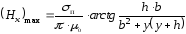. (2.41)

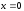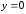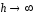Если ,и, то.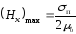

Составляющая 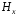проходит через ноль в точках

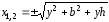. (2.42)

Составляющая 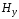проходит через ноль при 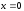и имеет экстремумы при

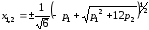, (2.43)

где 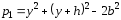;Формула (2.43) не совсем удобна при использовании, но если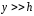и, то.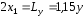

Несколько предельных случаев.

а) 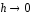(царапина). Если принять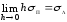, то формулы (2.38), (2.39)

переходят в формулы для двух равномерно заряженных нитей:

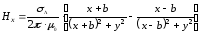, (2.44)

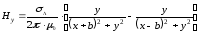. (2.45)

Можно отметить, что при этом .

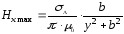Если 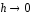и, а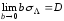, то мы имеем одну дипольную нить

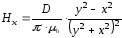; (2.46)

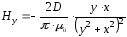. (2.47)

При этом 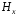обращается в 0 при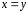, а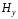 имеет экстремум при 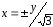. Следует отметить, что рассмотренный случай (т.е. царапина) редко представляет интерес с точки зрения магнитной дефектоскопии.

б) 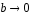(трещина с малым раскрытием). Это тот случай, который почти всегда выполняется на практике, поэтому его следует рассмотреть несколько подробней.

Для условия 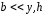формулы (2.38) и (2.39) можно разложить по малому параметру и пренебречь членами разложения с 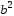и более высокими степенями. Получим

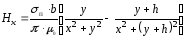, (2.48)

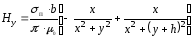. (2.49)

Это есть суперпозиция полей двух токов разного знака, расположенных в точках 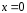,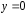и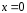,,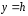 причем величина токов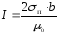.Графически эта суперпозиция показана на рис. 2.12.

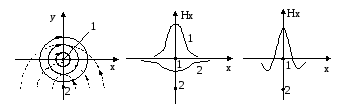
Рис. 2.12. Суперпозиция полей двух токов

а б в

Рис. 2.13. Мелкий (а), средний (б) и глубокий (в) дефекты

Изменение топографии поля с увеличением глубины дефекта можно

увидеть на рис. 2.13. Видно, что при 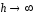экстремумы обратного знака

составляющей 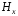исчезают.

Использование графической суперпозиции особенно эффективно при исследовании косорасположенных дефектов, то есть дефектов, расположенных к поверхности под углом, отличным от 90⁰. На рис. 2.14 показаны аппроксимации полей таких дефектов токами, расположенными в точках 1 и 2.

а б

Рис. 2.14. Составляющая поля косорасположенного дефекта

Из рис. 2.14 можно увидеть, что если длина дефекта (протяженность в направлении 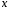)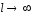, или глубина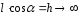_, то по топографии нельзя отличить наклонный дефект от нормального. Но в других случаях, если экстремумы ярко выражены, можно указать, над какой точкой поверхности находятся начало и конец дефекта.

_{На рис. 2.}15 представлены дефекты, часто встречающиеся на изделиях проката. Из рассмотренного выше следует, что поле дефекта АВС нельзя отличить от поля дефекта АС.

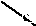
Рис. 2.15. Дефекты сложной формы

Поле наклонного дефекта можно выразить аналитически (при этом учтём, что поверхностная плотность зарядов наклонного дефекта ):

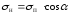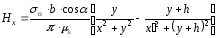, (2.50)

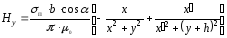, (2.51)

где .

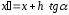Поскольку в (2.38) и (2.39) величина 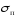не определена, то все приведенные формулы определяют только топографию поля дефекта, но не его величину. Чтобы составить представление о плотности зарядов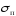, рассмотрим дефект в виде эллипсоида с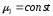в безграничном пространстве с(рис. 2.16).

Рис. 2.16. Эллипсоид в безграничном пространстве

Пусть среды 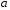и 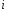перемагничиваются по следующим законам:

,

,

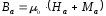что можно переписать в виде

,

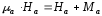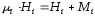. (2.52)

Поле 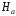определяется на большом расстоянии от эллипсоида. Вблизи эллипсоида это поле не будет однородным. Поле внутри эллипсоида однородно и во всех точках равно одной и той же величине.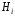

Для поля внутри эллипсоида справедливо

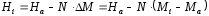, (2.53)

где 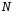- коэффициент размагничивания (см. 3.6).

На границе раздела сред

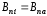. (2.54)

Из (2.52) следует

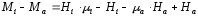. (2.55)

Выражение (2.54) можно переписать в виде

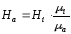. (2.56)

Из (2.55) с учётом (2.56) получим

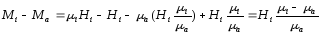. (2.57)

Подставив (2.57) в (2.53) получим:

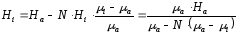. (2.58)

Выражение (2.58) определяет полное поле внутри эллипсоида. Вычтем из него 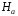и получим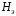- это собственное поле эллипсоида, то есть та добавка, которая образовалась из-за того, что ферромагнетик не однороден, а имеет эллипсоидальное включение с отличающимся значением проницаемости:

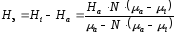. (2.59)

Поскольку 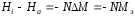следует, что намагниченность

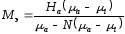. (2.60)

Здесь 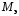- это намагниченность “эквивалентного магнита”, то есть такого магнита, который имеет на поверхности заряды, создающие поле, совпадающее с полем эллипсоида. Если эллипсоид пустой (полость), то проницаемость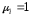, а намагниченность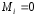. Тогда с учетом (2.52) можно записать:

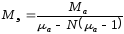. (2.61)

Учитывая, что коэффициент размагничивания эллипсоида (см. 3.6) равен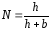, а плотность поверхностных зарядов численно равна намагниченностииз (2.61) получим:

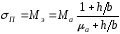. (2.62)

Из (2.62) можно увидеть, что

1. плотность поверхностных зарядов на стенках полого эллипсоида прямо пропорциональна намагниченности ферромагнетика;

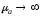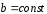2. при ( и 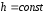) следует;

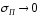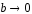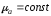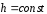3. при , узкая щель (и), следует.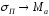

Формула (2.62) дает представление о зависимости зарядов на стенках дефекта от магнитных свойств среды и параметров дефекта.

Обратная задача магнитной дефектоскопии. Расчет магнитных полей дефектов по их известным параметрам является прямой задачей магнитной дефектоскопии. Определение параметров дефектов по их известному магнитному полю является обратной задачей магнитной дефектоскопии.

Обратные задачи являются некорректными, т.к. нужно определить большое число параметров из ограниченного числа данных. Для дефектов необходимо определить величину и форму дефекта, которая сама по себе характеризуется большим набором параметров (глубина, протяженность, раскрытие, угол наклона и т.д.).

Несмотря на сложность обратных задач в некоторых случаях удается найти их решение. Представим себе, что в изделии имеются только узкие поверхностные дефекты, к которым применимы формулы (2.50) и (2.51). Перепишем (2.50) в координатах, отнесенных к 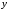(в данном случае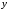– фиксированный зазор между поверхностью изделия и преобразователем):

.

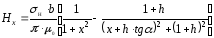Определив корни этого уравнения

,

сформируем разность и сумму

, ,

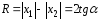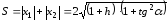откуда определяются искомые параметры:

, .

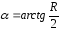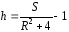Обратные задачи – а это есть основные задачи любого метода дефектоскопии – в общем виде не могут быть решены по указанным выше причинам, однако частные или приближенные (численные) решения могут быть найдены.