2. Превратив отрезок в прямую уровня, т.Е. Решив первую зада-

6.4

чу на преобразование, переходим к решению второй задачи.

Если предположить, что теперь ось вращения, перпендикулярная к плоскости V , совпадает с точкой А1, то поворотом вокруг этой оси мы можем отрезку А1В1, придать проецирующее положение А₂В₂ относительно плоскости Н.

Решение третьей задачи - преобразование плоскости общего положения в проецирующую_, покажем на примере плоскости , заданной следами /рис. 6.4/.

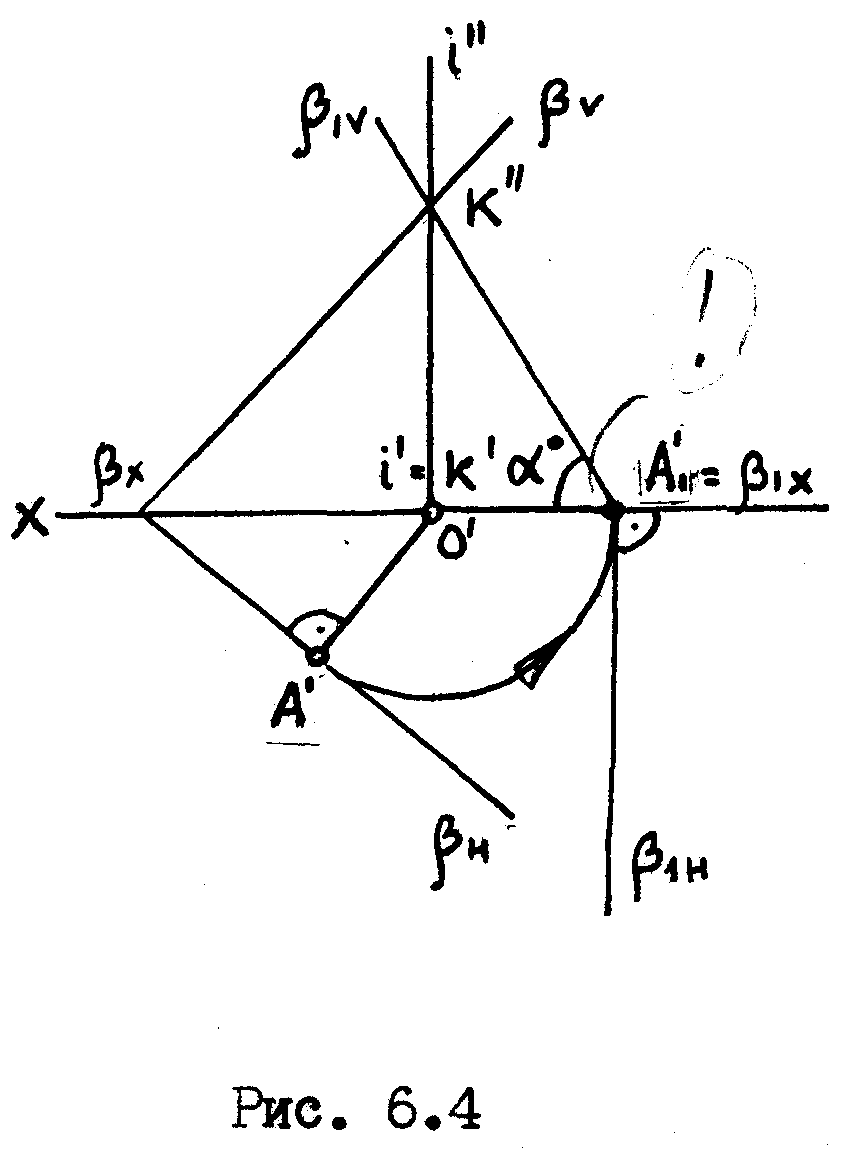Сделаем эту плоскость фронтально проецирующей. Для упрощения построения ось вращения l выбрана так, что она лежит, в самой плоскости V и потому пересекает, след в некоторой точке К. Эта точка не будет изменять своего положения при вращении плоскости вокруг оси. Так как плоскость должна быть фронтально-проецирующей, то, очевидно, нужно повернуть ее горизонтальный след _н так, чтобы он стал перпендикулярным к оси X. Для выполнения на эпюре этой операции проведем и повернем проведенный перпендикуляр вместе со следом до горизонтального положения, т.е. до совпадения с осью X. Тогда точка а'переместится в и след займет требуемое положение . Новое положение фронтального следа

соединив точку с неподвижой точкой к".

Превратив плоскость во фронтально-проецирующую, на плоскости V мы будем видеть в натуральную величину угол наклона этой плоскости к плоскости проекций Н - угол .

Последовательное решение третьей и четвертой задачи на пре-образование чертежа рассмотрим на примере плоскости, заданной треугольником АВС /рис. 6.5/. Вначале треугольник АВС поворачиваем вокруг заданной оси l до положения фронтально-проецирующей плоскости. Для этого поворачиваем предварительно построенную горизонталь треугольника АD до положения, при котором она станет перпендикулярной к плоскости V. Новая горизонтальная проекция треугольника будет конгруентна прежней

6.5

Затем, вращая треугольник около оси, перпендикулярной к плоскости V и совпадающей с точкой С1,до положения горизонтальной плоскости, придадим ей положение плоскости уровня.

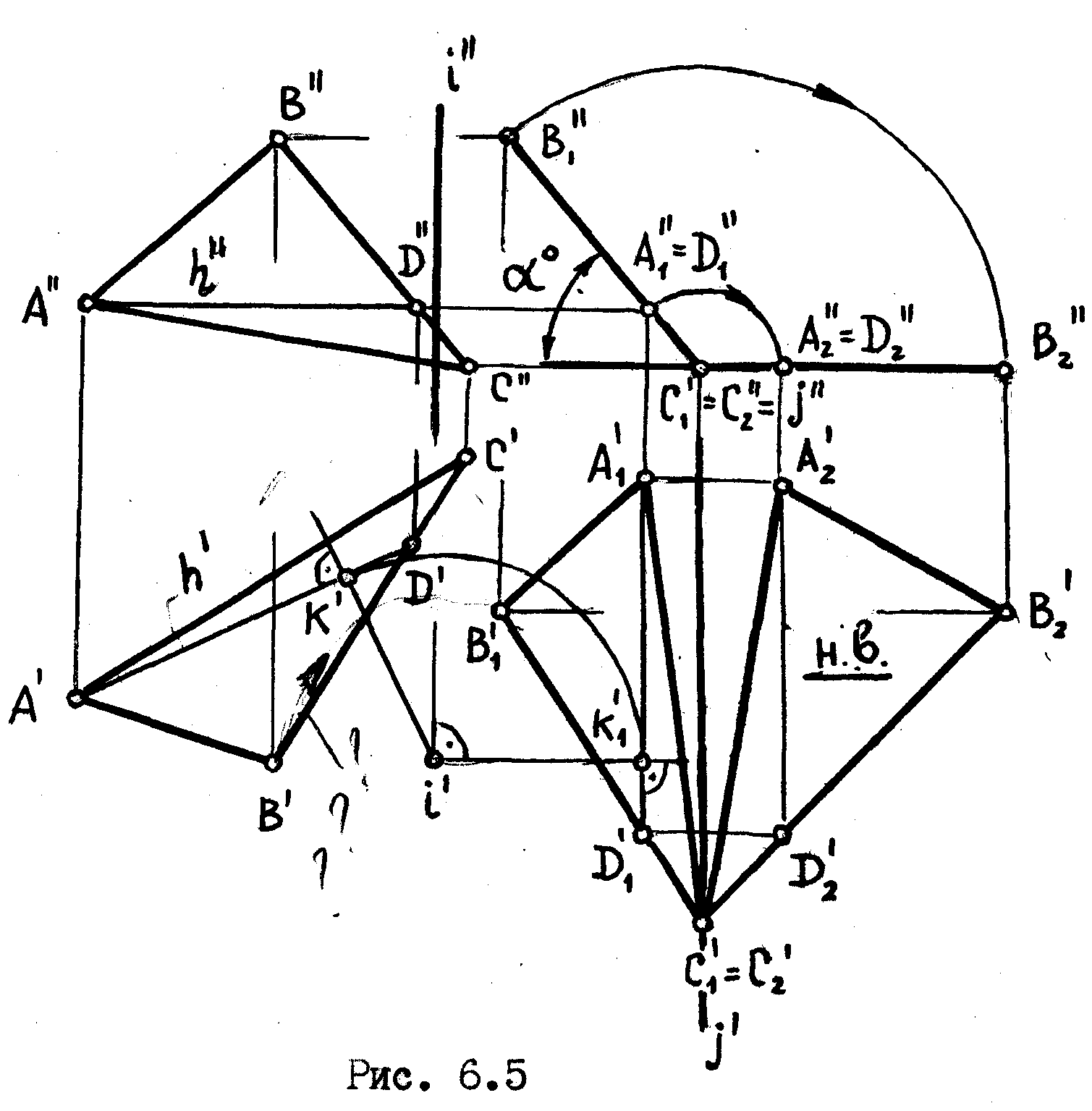В последнем случае горизонтальная проекция треугольника будет представлять его натуральную величину .

Отметим, что, как и, в предыдущих случаях, для того, чтобы решить

4-ю задачу на преобразование приходится попутно решать 3-ю задачу.

6.2 Способ вращения вокруг оси, параллельной плоскости проекций.

Вначале рассмотрим вращение точки А вокруг оси 1, параллельной плоскости Н /рис. 6.6/. Вращение точки А происходит в пространстве по окружности, плоскость которой перпендикулярна к оси вращения и к плоскости Н. Эта окружность проецируется на плоскость Н в виде прямой линии , образующей прямой угол с проекцией оси вращения. Следовательно, при повороте точки А

6.6

вокруг оси l , ее горизонтальная проекция будет передвигаться по прямой , но эта прямая теперь уже не параллельна оси X, как это имело место раньше /п. 6.1/.

Так как окружность, которую описывает в пространстве точка А, не параллельна плоскости V , то она будет проецироваться на эту плоскость в искаженном виде /в виде эллипса/. Следовательно, фронтальная проекция точки А будет перемещаться не по окружности, а по дуге эллипса, точное построение которой представляет известные трудности. Однако при решении некоторых частных вопросов можно обойтись одной горизонтальной проекцией точки /или фигуры/, не прибегая к построению ее фронтальной проекции.

Допустим, например, что вращение точки А остановлено в тот момент, когда она пришла в положение , при котором радиус R параллелен плоскости Н, т.е. когда точка А с о в м е щ а е т с я с некоторой горизонтальной плоскостью, проходящей через ось вращения.

В этом положении радиус проецируется на плоскость Н в натуральную величину. Значит, для нахождения горизонтальной проекции достаточно отложить на прямой отрезок .

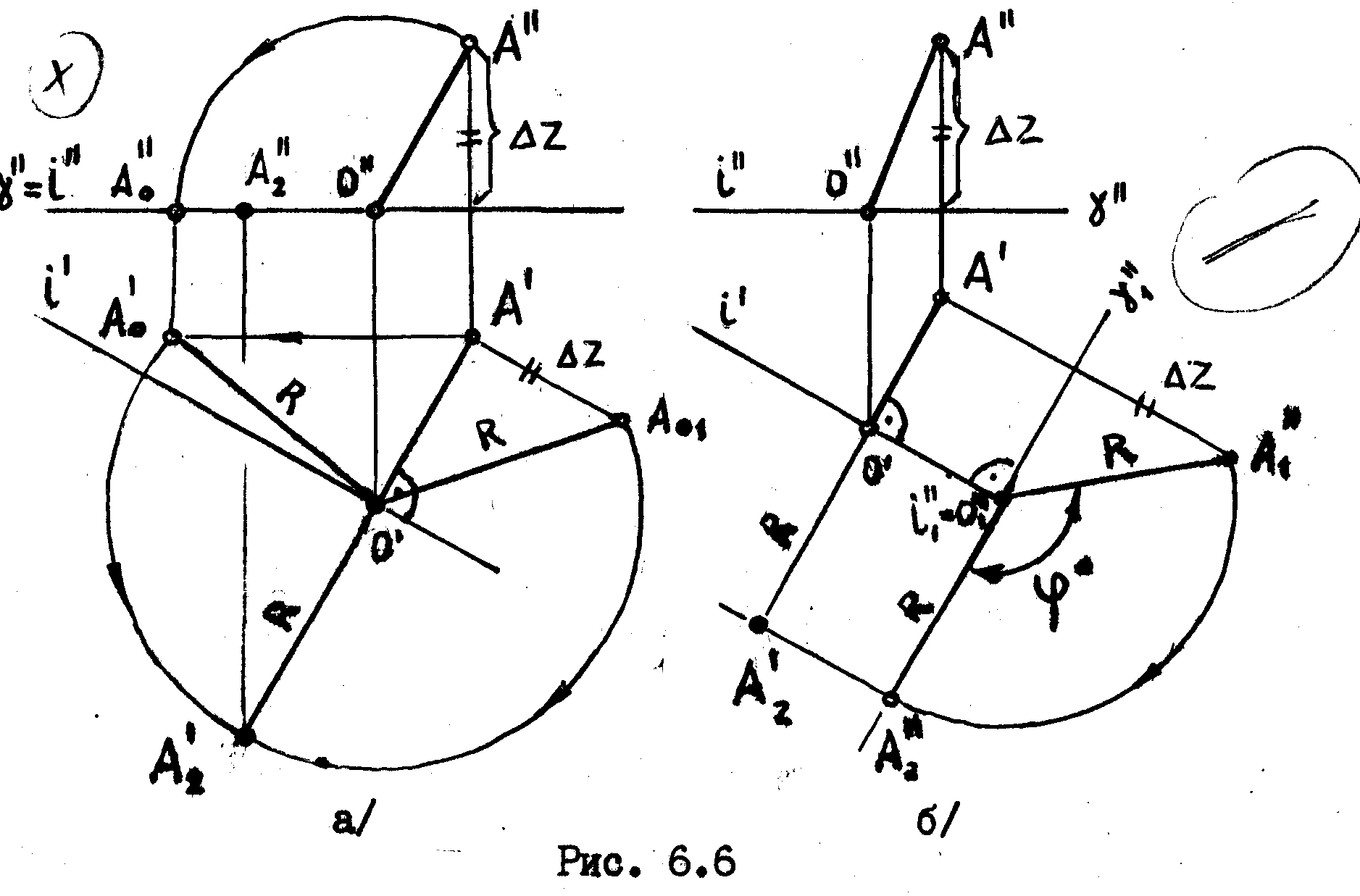
На рис.6.6а показано, как выполняются эти построения на эпюре. Здесь даны проекции а' и А” произвольной точки и проекции оси, параллельной плоскости Н – l’ и l”. Требуется повернуть точку А вокруг оси l настолько, чтобы она совпала с горизонтальной

6.7

плоскостью, проходящей через l . Из вышесказанного следует, что для, того, чтобы построить новое повернутое положение точки, необходимо предварительно построить натуральную величину Н по его проекциям. Это может быть сделано любым из известных нам способов.

На рис.6.6а показаны два способа: 1/построение натуральной величины Н известным нам способом прямоугольного треугольника, гипотенуза которого и есть R; 2/поcтроение натуральной величины R вращением отрезка ОА вокруг оси, перпендикулярной к плоскости V. Отложив этот отрезок R, найденный первым или вторым путем, на прямой , найдем искомую проекцию .

Натуральную величину R можно найти также введением дополнительной плоскости проекций V1/рис.6.6б/.

Обычно этим способом не пользуются, т.к. он графически более трудоемок, чем случаи, приведенные на рис. 6.6а. Однако при этом способе, мы можем увидеть на какой угол, при этом, мы поворачиваем точку А. Этим углом будет угол .

Введение дополнительной плоскости проекций совершенно необходиио в тех сдучаях, когда по условию задачи нам предстоит повернуть точку А на наперед заданный угол , отличный от показанного угла .

Способ вращения вокруг оси, параллельной плоскости проекций особенно широко применяется при решении четвертой задачи на преобразование чертежа, т.е. при преобразовании плоскости общего положения в плоскость уровня. При таком преобразовании все фигуры, лежащие в плоскости, будут проецироваться в натуральную величину. Особое преимущество настоящего способа преобразования перед ранее рассмотренными, состоит в том, что он наиболее рационален из них, т.к. этот способ переводит плоскость общего положения в плоскость уровня, минуя предварительный ее перевод в плоскость проецирующую, что было совершенно необходимо во всех предыдущих способах.

По этой причине задачи на определение истинных величин фигур и углов решаются преимущественно этим способом.

В качестве примера подобной задачи рассмотрим следующий пример.

Вращением около горизонтали, т. е. прямой, параллельной плоскости Н, найти натуральную величину заданного треугольника АВС,

/ рис. 6.7 /.

Построив в плоскости треугольника горизонталь СD, принимаем ее за ось вращения. Используя опыт вращения отдельной точ-

6.8

ки А /рис. 6.6/ находим повернутое положение вершин треугольника.

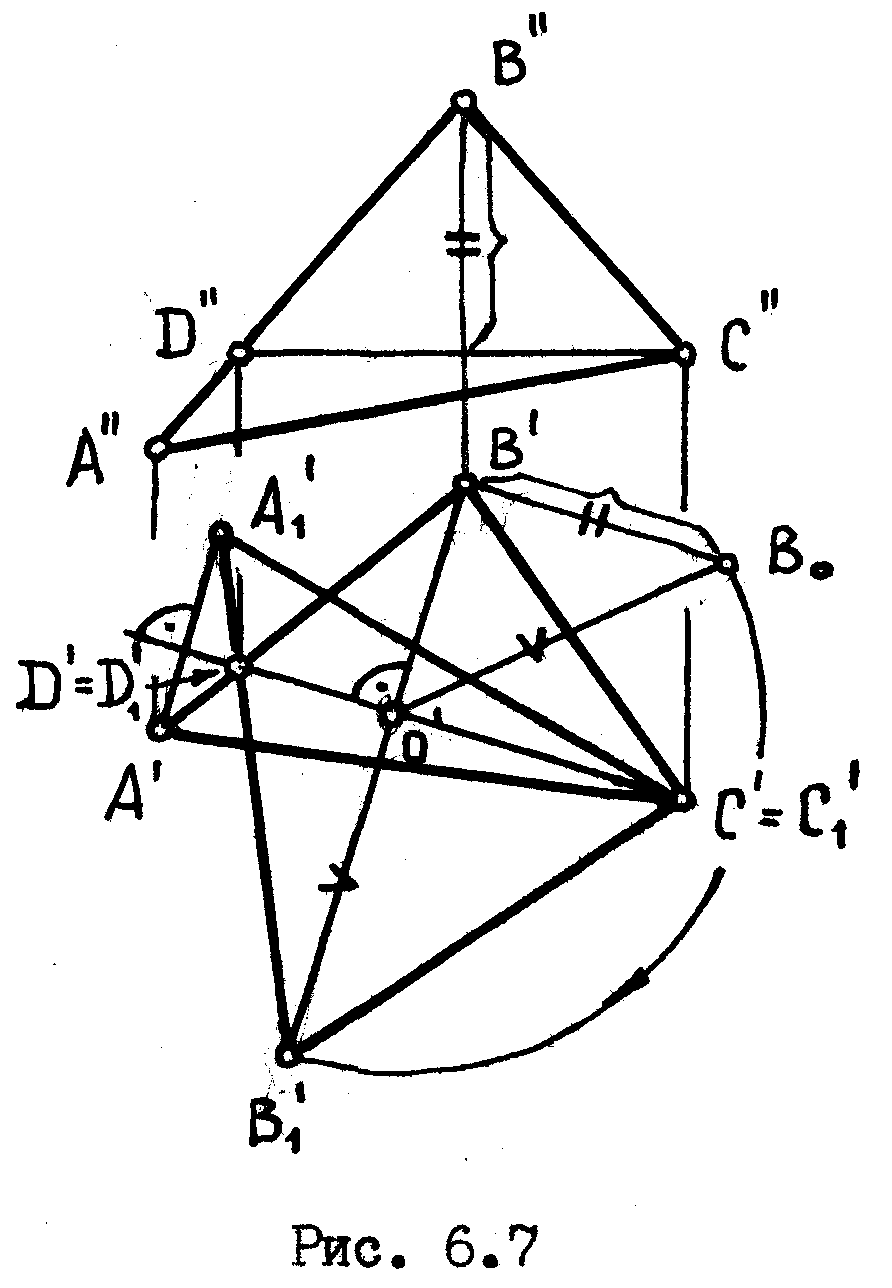Строим повернутое положение вершны В - точку В’, предварительно найдя способом прямоугольного треугольника натуральное значение радиуса вращения этой точки, .

Вершина треугольника С, как лежащая на оси вращения, останется неподвижной.

Повернутое положение вершны А найдем из двух следующих условий.

1. Горизонтальная проекция окружности, по которой будет перемещаться вершина А, будет представлять прямую, перпендикулярную к оси вращения. Строим эту прямую.

2. Сторона АВ в повернутом положении, как и до поворота , будет проходить через точку D . Точка D в процессе поворота остается неподвижной, т.к. она лежит на оси вращения. Проводим прямую .

Пересечение прямых, найденных из этих двух условий, дает нам новую горизонтальную проекцию повернутой вершины А - точку . Соединяя вершны получаем новую горизонтальную проекцию треугольника

АВС, плоскость которого параллельна плоскости Н. Следовательно треугольник представляет собой натуральную величину заданного треугольника

.

6.9

Содержание лекции №6 изложено в учебнике С.А.Фролова на стр. 98 - 104 .

Локтев О.В. стр.47-53, 99-104

7.1

РАЗДЕЛ № 3

Метрические задачи / Лекции № Р 7-9 /.

Лекция №7

Тема лекции

Перпендикулярность прямых и плоскостей.

Содержание лекции.

Свойства проекций плоских углов. Особенности проекции прямого угла. Прямая, перпендикулярная плоскости.

Взаимная перпендикулярность прямых. Взаимная перпендикулярность плоскостей.

7.1 Свойства проекций плоских углов.

Для понимания темы настоящей лекции, а также при решении метрических задач на определение истинных /натуральных/ значений углов, с которыми мы познакомимся на ближайших лекциях, необходимо запомнить следующие несложные положения.

7.1.1. Если обе стороны любого /острого, прямого или тупого/ угла параллельны плоскости проекций, то на эту плоскость проекций этот угол спроецируется без искажений, т.е. в натуральную величину, /см. рис.7.1/.

7.1.2 Если стороны угла не параллельны плоскости проекций, то этот угол проецируется на эту плоскость с искажением,/см. рис.7.2

7.2

При этом, проекция угла может быть меньше / на рис. 7,2а /, а может быть и больше /рис.7.2б/ истинного значения угла.

Примечание. Вращая циркуль или две рейки, образующие угол, показать студентам, что любой угол может проецроваться углом, величина которого может меняться от 0°до 180°.