3. Рассмотрим решение двух задач из этой группы.

Задача.

Определить расстояние между параллельными плоскостями и .

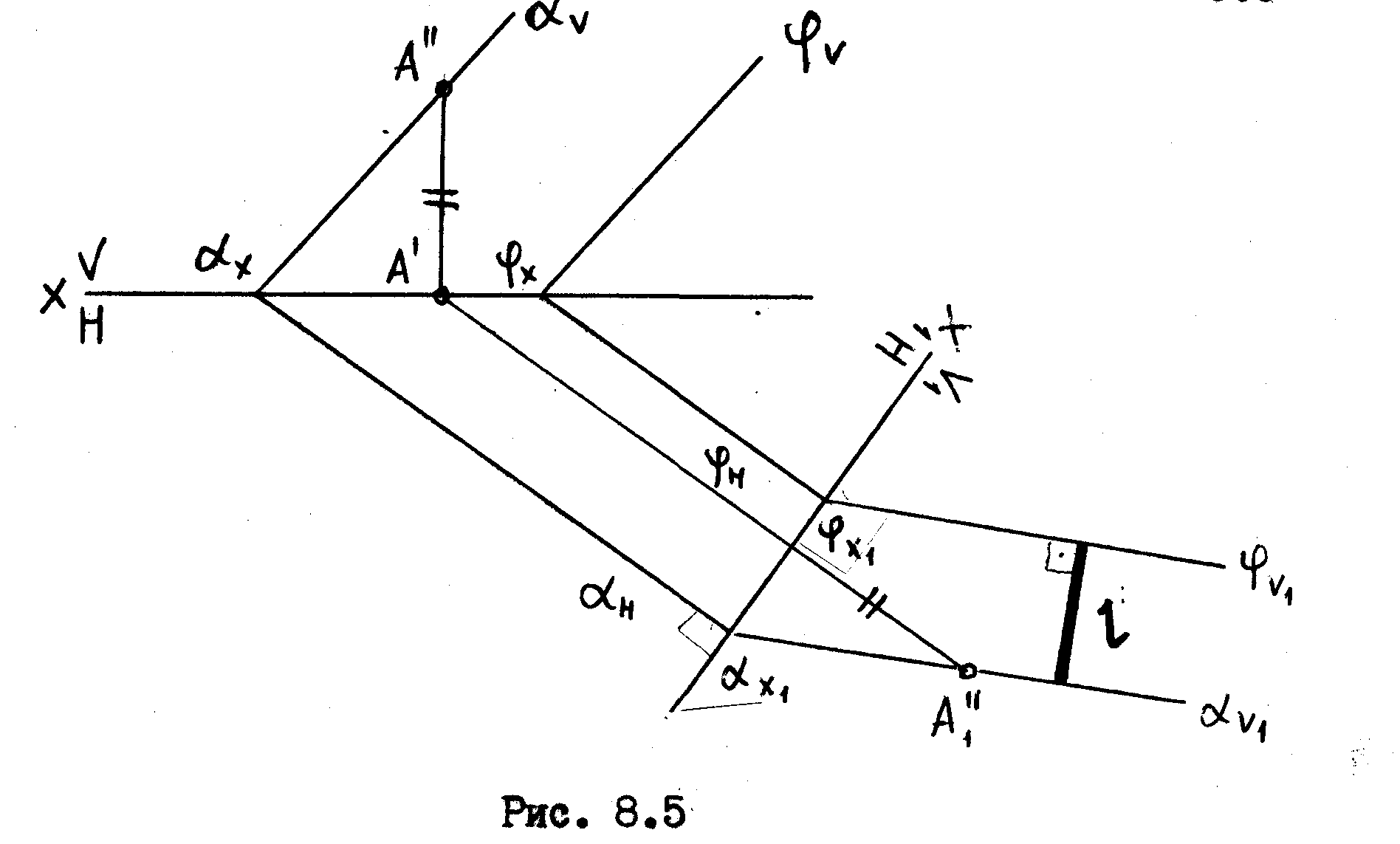
8.5

Преобразуя заданные плоскости в проецирущие, опрвделяем натуральную величину расстояния между ними.

Задача

Дано: треугольник АВС и фронтальная проекция треугольника DEF, плоскость которого параллельна плоскости треугольника АВС. Построить горизонтальную проекцию треугольника DEF, если известно расстояние между плоскостями треугольников, равное отрезку l.

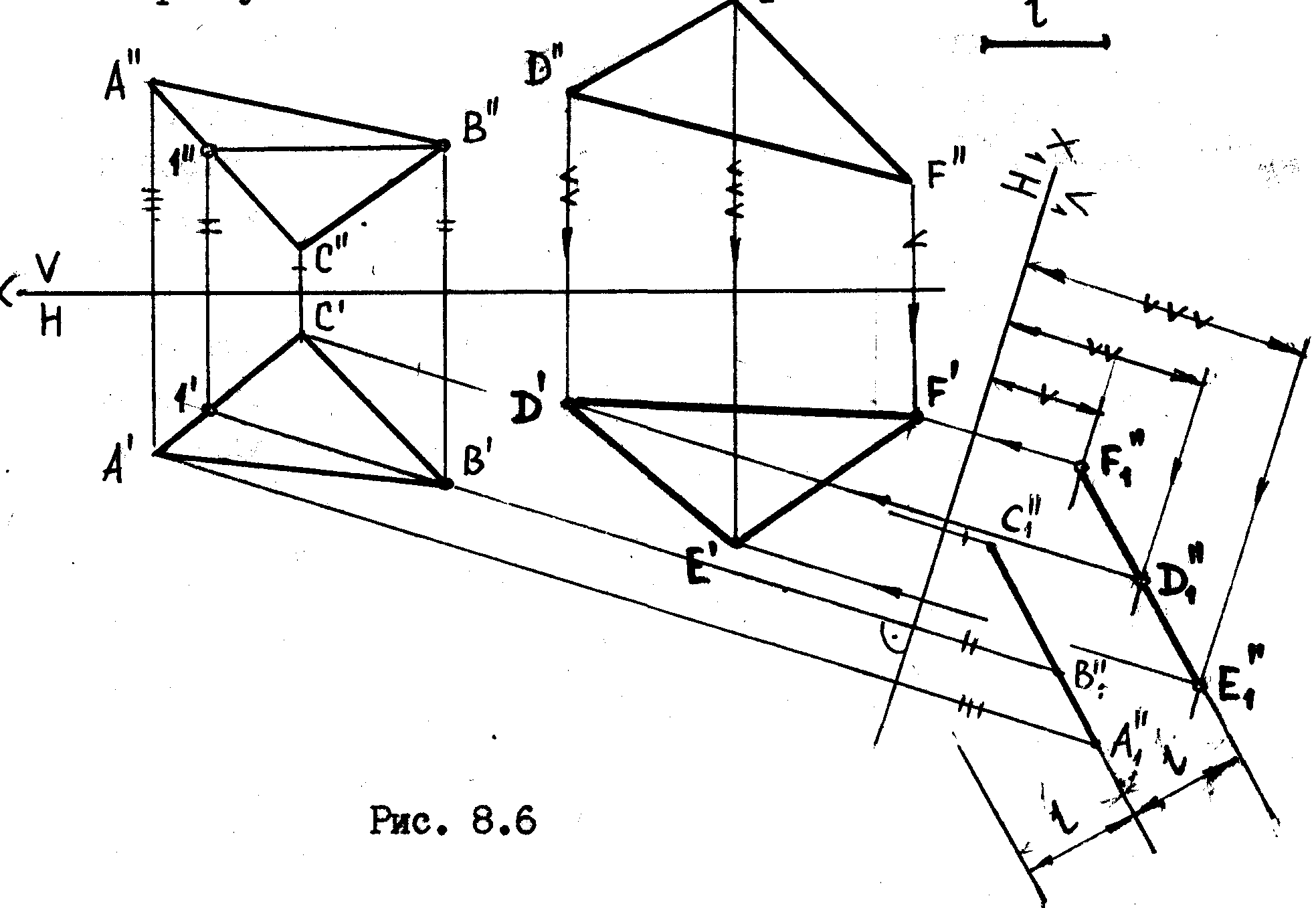
8.6

5. Решение

Также, как и в предыдущей задаче, для того, чтобы видеть натуральную величину расстояния между плоскостями треугольников, их плоскости превращаем в проецирующие. Как видим, задача имеет два решения. Для ясности чертежа следует показать только одно из этих решений. Получив новую фронтальную проекцию треугольника DEF на плоскости V1, находим горизонтальные проекции его вершин, как точки пересечения соответствующих линий связи.

Содержание лекции №8 изложено в учебнике С.А.Фролова /изд. 1978 г./ на стр. 183 - 189.

9.1

ЛЕКЦИЯ №9

Тема лекции.

Определение действительной /натуральной/ величины углов.

Содержание лекции.

Определение угла между прямыми. Определение угла между прямой и плоскостью. Определение угла между плоскостями.

9. Определение действительной величины углов.

Должны быть рассмотрены следующие три задачи.

I.Определение угла между двумя пересекащимися прямыми.

2.Определение угла между прямой и плоскостью.

З.Определение угла между двумя плоскостями.

9.1. Определение натуральной величины угла между двумя пересекающимися прямыми.

Для того, чтобы угол между прямыми спроецировался в натуральную величину необходимо, чтобы обе стороны этого угла были параллельны данной плоскости проекций, т.е. чтобы плоскость угла была плоскостью уровня.

При решении этой задачи наиболее рациональным, а поэтому, наиболее распространенным путем решения,является преобразование чертежа способом вращения плоскости вокруг одной из ее прямых уровня /см. лекцию №6/. При итом способе плоскость общего положения сразу преобразуется в плоскость уровня.

Задача

Определить истинное значениве угла между пересекающимися прямыми m и n. /рис. 9.1/.

Решение

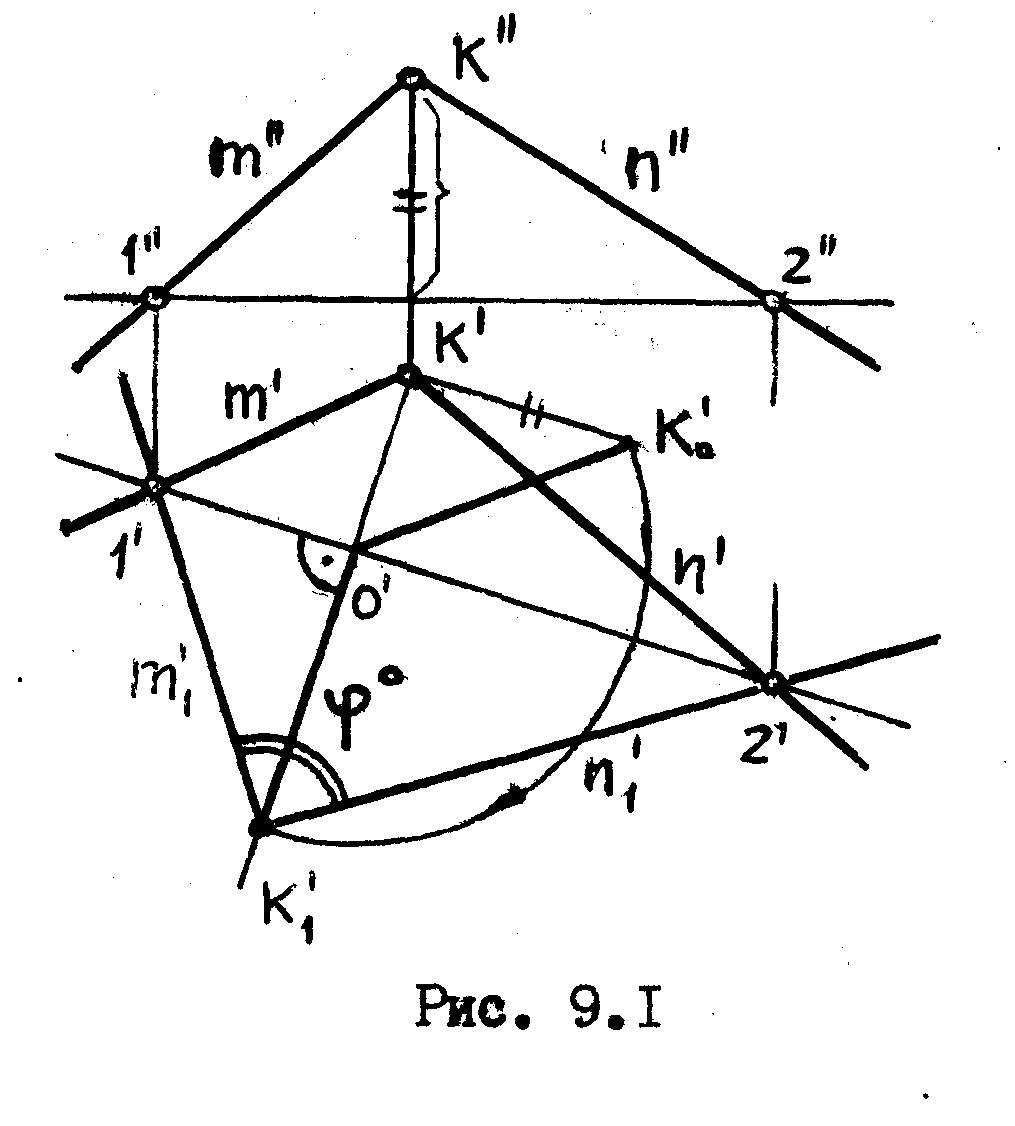В плоскости угла строим произвольную горизонталь /1,2/. Вращая треугольник 1К2 вокруг этой горизонтали до положения, параллельного плоскости

9.2

Н, находим его натуральную величину и, следовательно, натуральную величину искомого угла при вершине К – угла

9.2 Определение натуральной величины угла между прямой и плоскостью.

Угол между прямой и плоскостью можно определить двумя различными путями.

1. Путем определения непосредственно самого угла.

2. Путем определения дополнительного угла.

На примере решения двух следующих задач, познакомимся с тем и другим путем решения. При решении первой задачи отыщем непосредственно угол - угол между прямой и плоскостью.

Задача I.

Определить угол между прямой ВD и плоскостью треугольника АВС /рис. 9.2/.

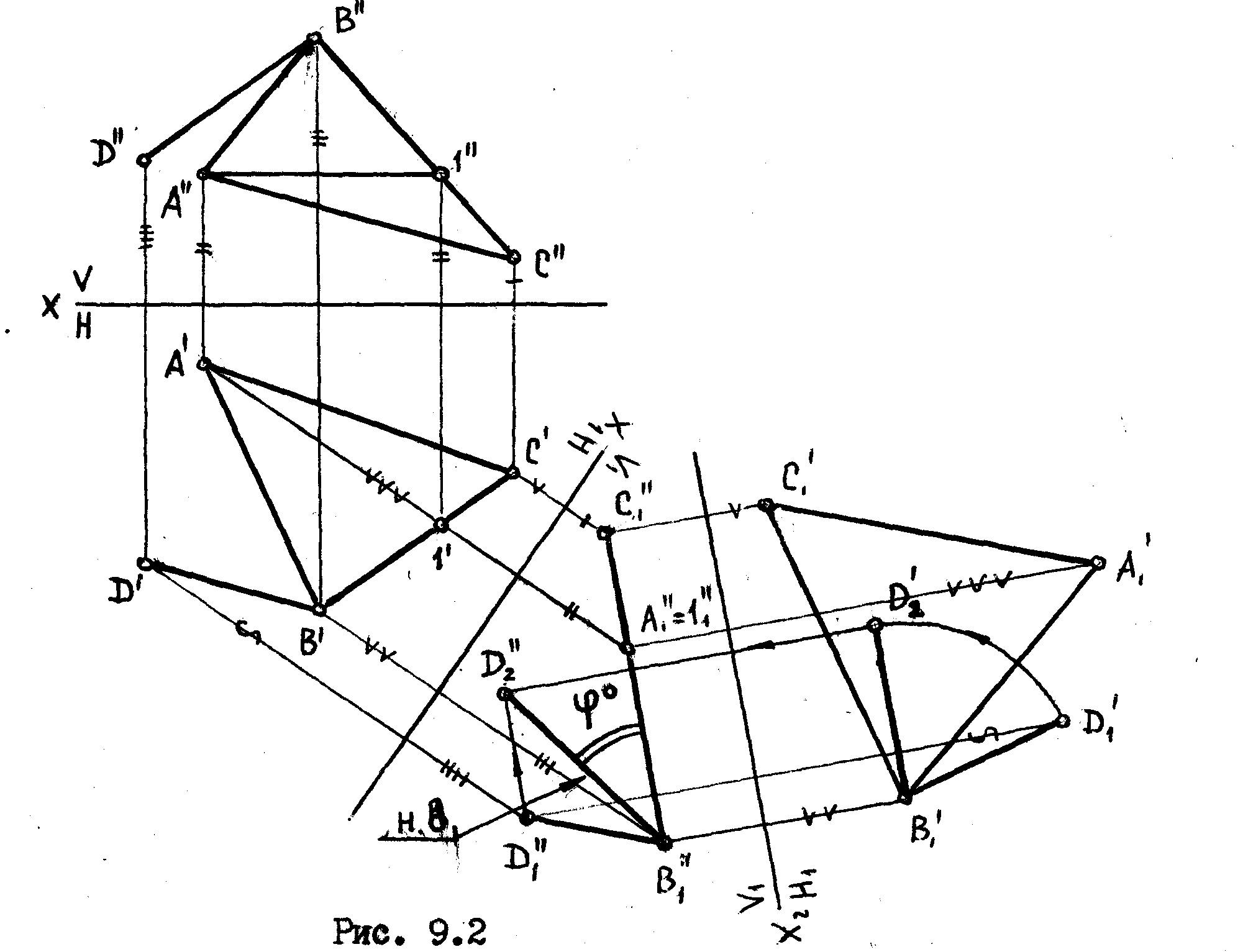
Угол между прямой и плоскостью спроецируется в натуральную величину на одну из плоскостей проекций в том случае, если заданная плоскость будет по к этой плоскости проек -

9.3

ций проецирущей, а прямая - прямой уровня, т.е будет параллельной этой плоскости проекций.

Преобразуя чертеж с целью достижения такого расположения плоскости и прямой, следует следить за тем, чтобы в результате такого преобразования не произошло относительного перемещения прямой и плоскости, при котором искомый угол изменит свою величину.

Решение

Вводим новую плоскость проекций V1, по отношению к которой плоскость треугольника АВС будет проецирующей. Однако, угол между прямой ВD и плоскостью треугольника не будет проецироваться на V1, в натуральную величину, т.к. прямая ВD не будет параллельна плоскости V1. Введем еще новую плоскость проекций Н₁, параллельную плоскости треугольника. В системе плоскостей проекций плоскость треугольника стала горизонтальной плоскостью.

Теперь мы можем повернуть прямую ВD вокруг оси, перпендикулярной к Н₁ до положения, при котором она станет параллельной плоскости V1. Поскольку ось вращения, перпендикулярная к Н₁ , будет, одновременно, перпендикулярна к плоскости треугольника, то при таком вращении прямой, ее угол наклона к плоскости треугольника не будет менять свою величину.

Повернув прямуго ВD до положения, параллельное V1, мы добились того, что угол между прямой ВD и плоскостью треутольника АВС спроецируется на эту плоскость проекций в натуральную величину.

К решению задачи на определение угла между прямой и плоскостью можно подойти с иных позиций. Из рис. 9.3 мы видим, что если прямая 1 образует с плоскостью угол , то та же прямая 1 с перпендикуляром к этой плоскости - прямой n образует угол .

Поскольку треугольник АВС прямоугольный, то сумма углов и равна прямому углу, т.е .

В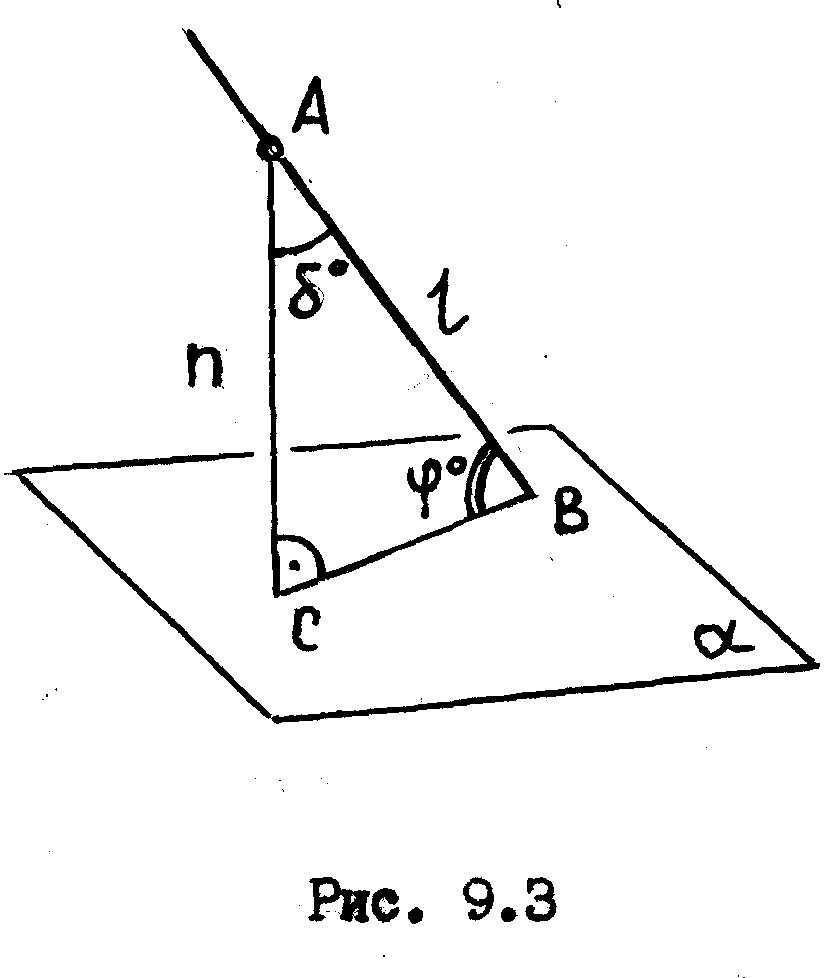 идим, что угол дололняет угол до .

9.4

Эта простая зависимость позволяет нам, в некоторых задачах на отыскание угла между прямой и плоскостью, отыскивать не сам угол , а дополнительный угол .

Рассмотрям такую эадачу.

Задача 2

Определить натуральную величину угла между прямой l и плоскостью заданной следами /рис. 9.4

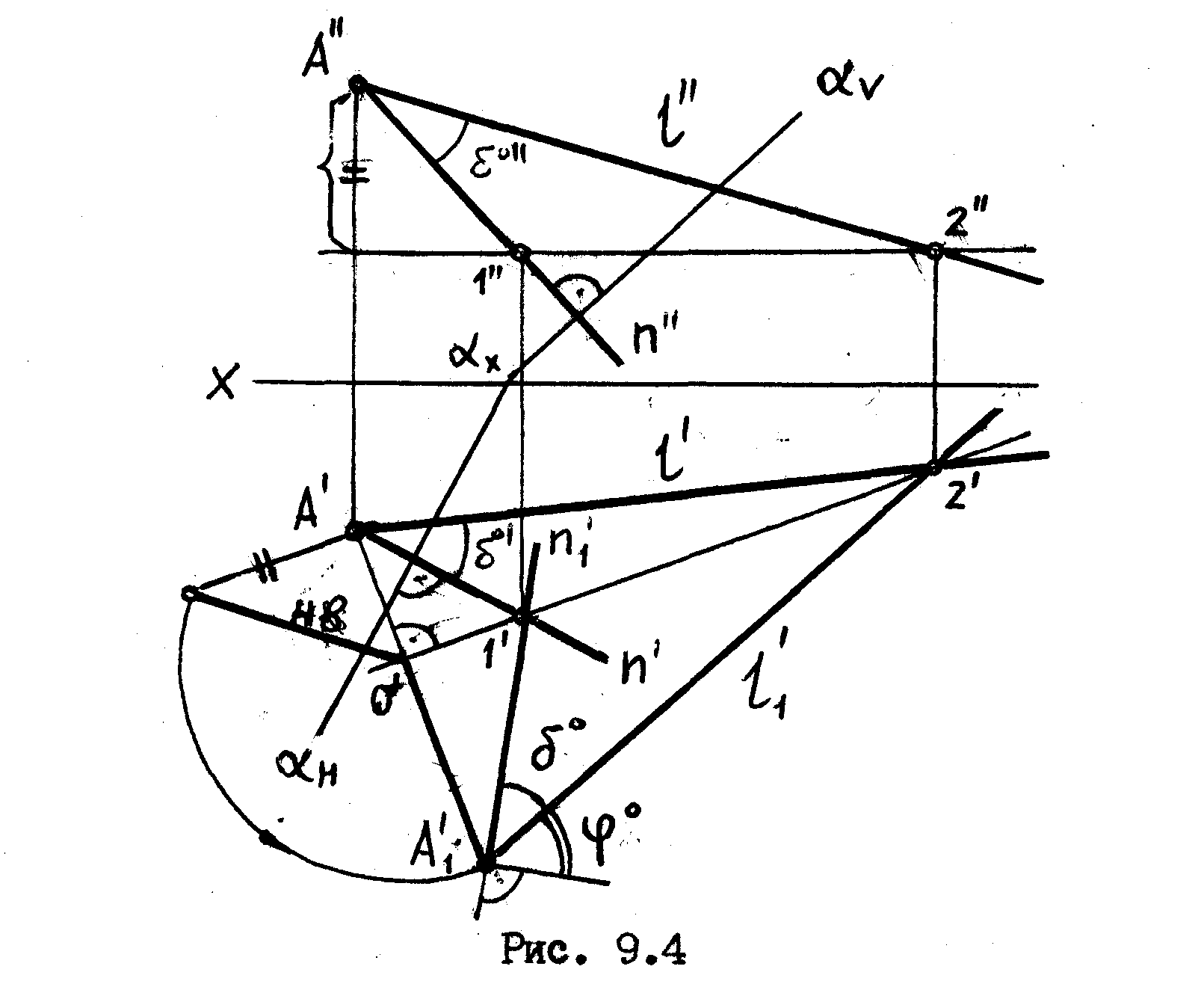
Решение

Взяв на пряной 1 произвольную точку А, опускаем из этой точки перпендикуляр на плоскость - прямую n. Угол между прямыми 1 и n и будет искомым углом . Проводим в плоскости этого угла произвольную горизонталь 1-2. Затем, вращая треугольник 1А2 вокруг стороны 1-2, находим /как в задаче 9.1/ его натуральную величину, а с ней и натуральную величину угла . Угол, дополняющий угол до 90 , и будет углом , который нам требуется определить по услдвию задачи.

Последний путь решения можно применять не только в тех случаях, когда плоскость задана следами. В общем случае, в плоскости, как бы она не была задана, всегда можно провести горизонталь и фронталь. Наличие этих прямых: позволит нам ле-

9.5

гко провести перпендикуляр к этой плоскости, а затем, как в настоящем примере, определить угол , а затем, и угол .

9.3 Определение натуральной величины угла между плоскостями.

Эта задача, как и предыдущая, может быть решена двумя путями.

1. Путем определения непосредственно самого угла.

2. Путем определения дополнительного угла. Вначале рассмотрим первый путь решения.

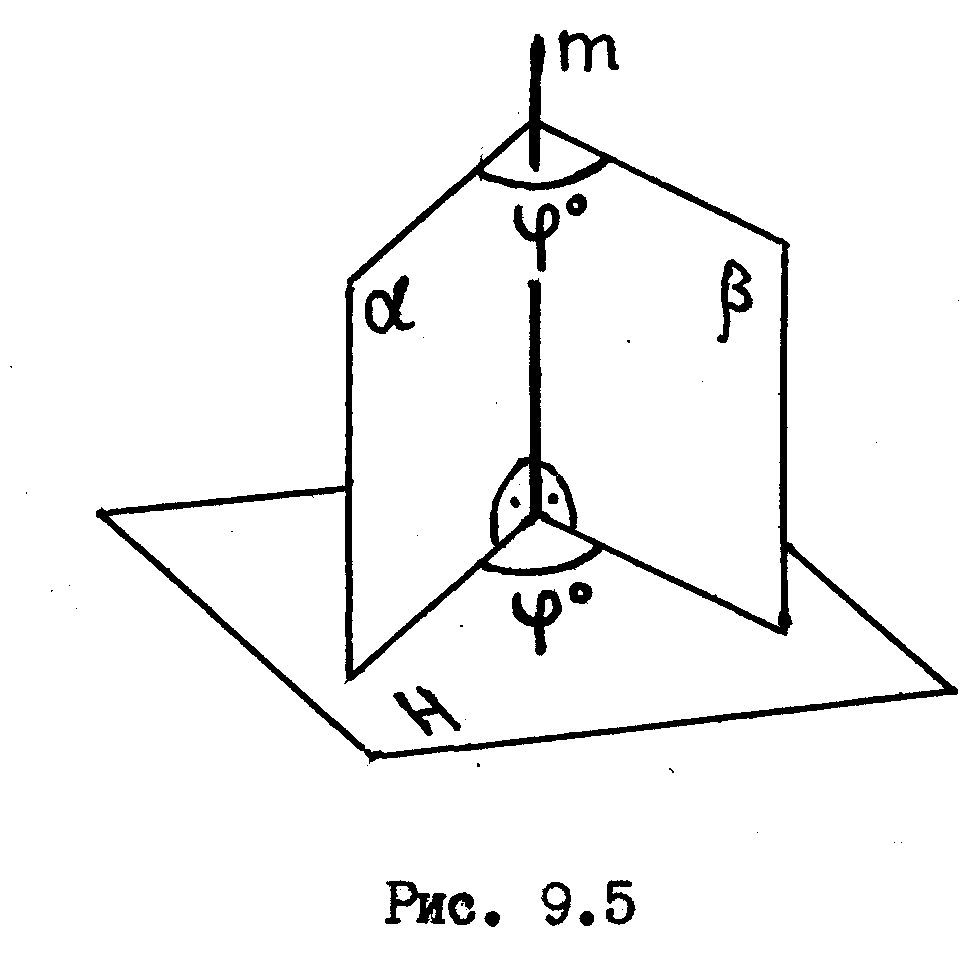
Двугранный угол между плоскостями и /рис.9.5/ будет проецироваться на одну из плоскостей проекций в натуральвую величину в том случае, если линия пересечения этих плоскостей - прямая m будет перпендикулярна к этой плоскости проекций.

В том случае, если, по условиям задачи, прямая m окажется прямой общего положения, то чертеж следует

преобразовать так, чтобы прямая m стала проецирующей /2-ая основная задача на преобразование чертежа/.

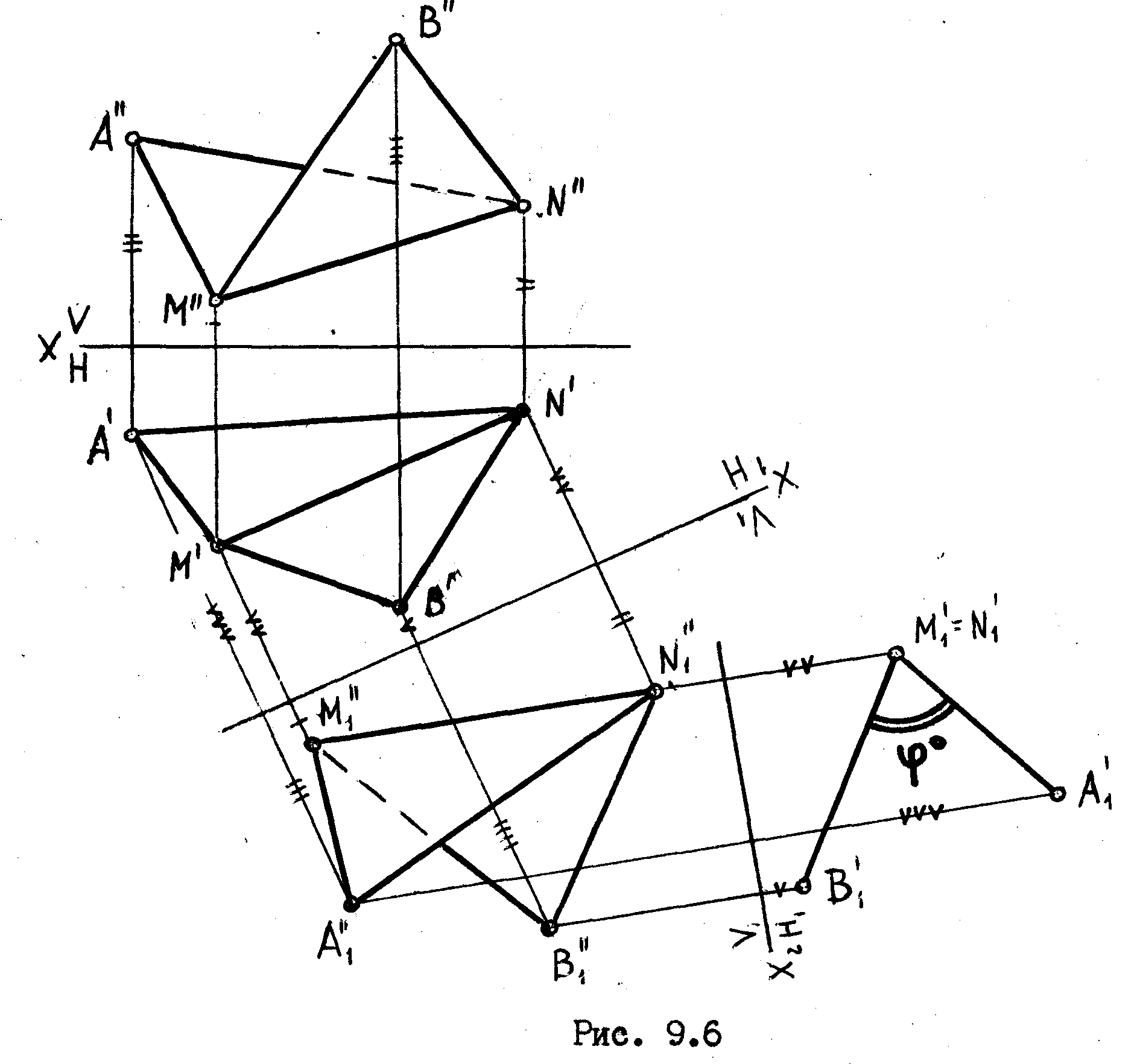
Задача I

Определить натуральную величину угла между треугольниками АМN и ВМN /рис. 9.6/.

Решение

В данной задаче нет необходимости отыскивать линию пересечения плоскостей, т.к. такая линия на чертеже уже есть - ею является общая сторона треугольников - прямая МN. Преобразуем чертеж способом замены плоскостей проекций. В новой системе плоскостей проекций - прямая МN становится горизонтально - проецирующей прямой, а плоскости треугольников - горизон тально-проецирущими плоскостями. Угол , который мы видим на плоскости Н , является мерой натуральной величины двугранного угла между заданными треугольниками.

9.6

Теперь рассмотрим второй путь решения задачи, при котором отыскивается не угол - угол между плоскостями, а угол -угол между перпендикулярами к этим плоскостям. Такой путь решения в некоторых случаях является более рациональным.

Из рис. 9.7 мы видим, что угол между перпендикудярами m и n, проведенными к плоскостям и через произвольную точку А, в сумме с искомым углом составляет . Т.е. можно сказать, что угол дополняет угол до . Отсюда становится очевидным, что, зная угол мы всегда сумеем легко определить и угол .

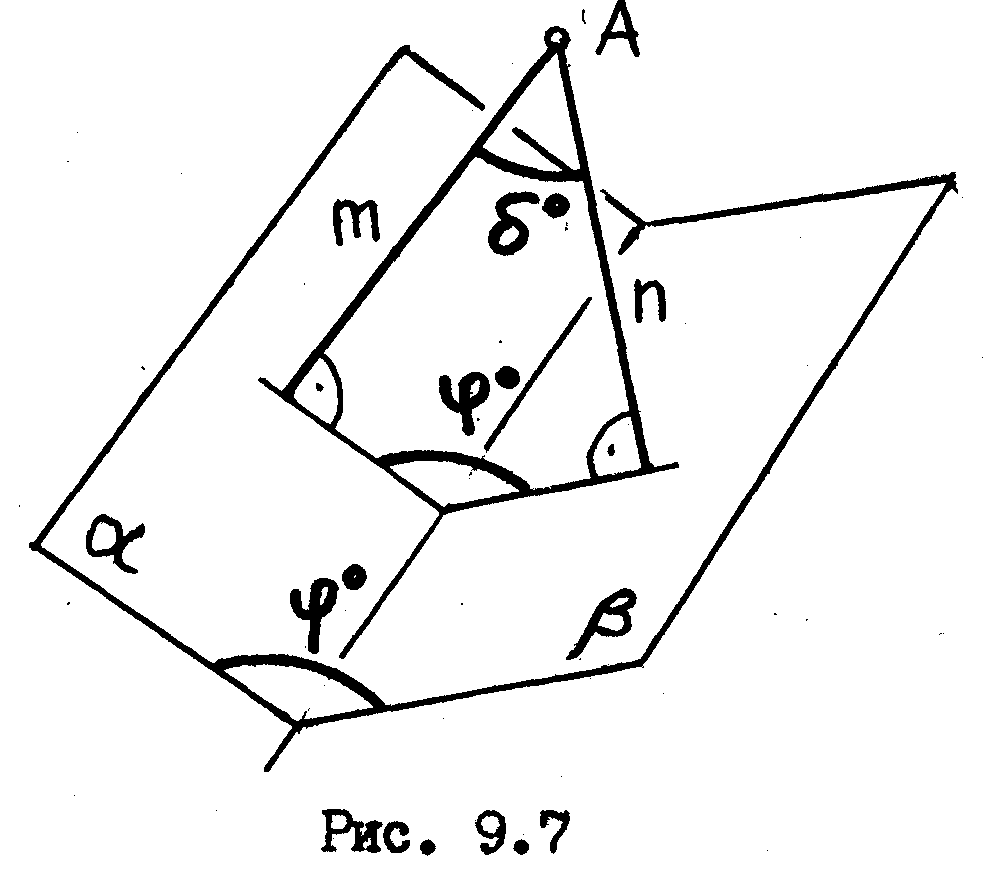
9.7

Рассмотрим этот путь решения на примере следующей задачи.

Задача 2

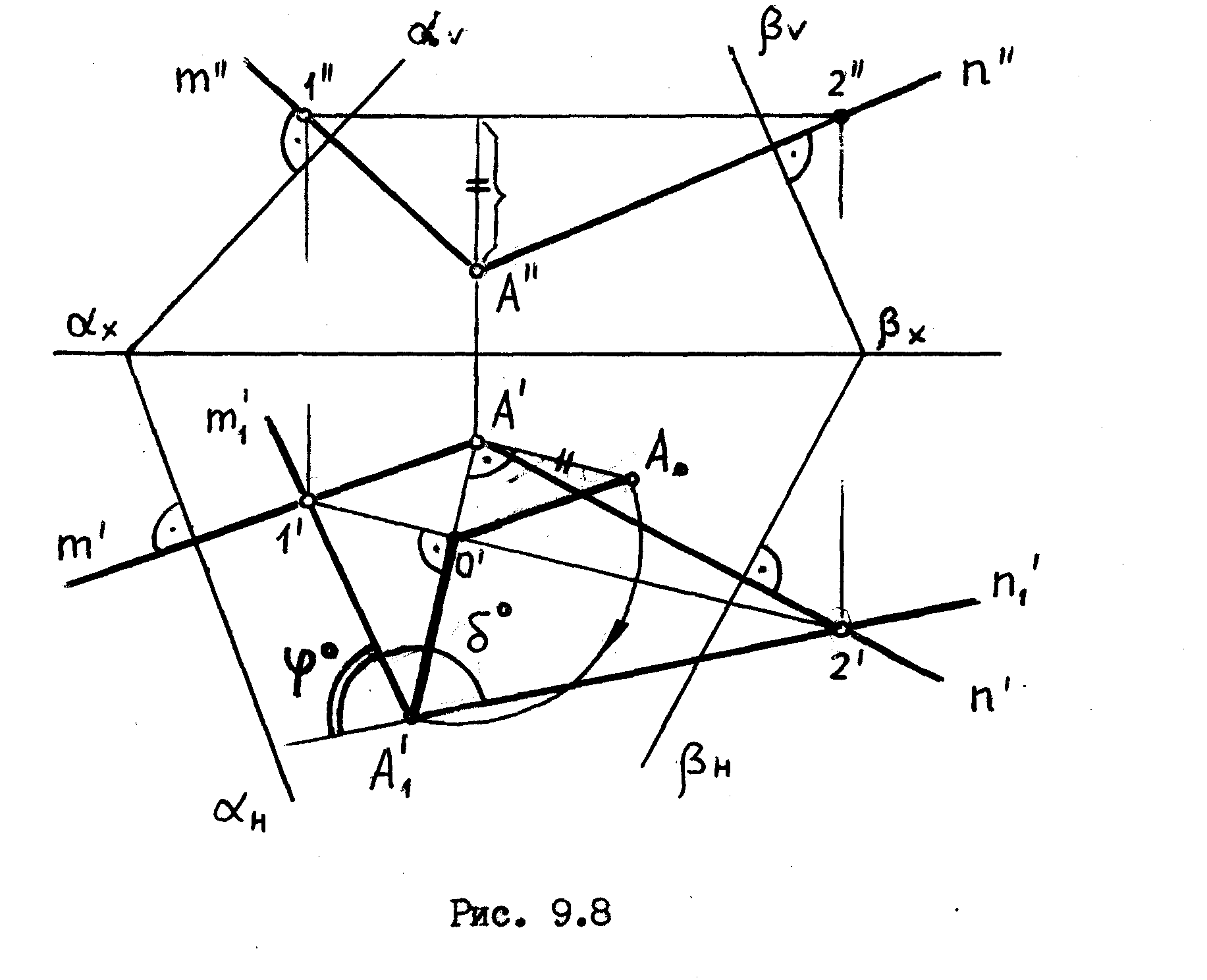Определить натуральную величину угла между плоскостями и рис. 9.8/.

Решение

Из произвольно выбранной точки А проводим перпендикуляры к заданным плоскостям: m - к плоскости , n - к плоскости . В плоскости, заданной перпендикулярами, проводим произвольную горизонталь 1-2. Путем вращения вокрут этой горизонтали определяем натуральную величину треугольника 1А2, а с ней и натуральную величину угла . Дополняя этот угол до , находим натуральную величину искомого угла .

Содержание лекции № 9 изложено в учебнике С.А.Фролова

/изд. 1978г./ на стр. 162-163, 168-172.

10.1

Р А З Д Е Л №4

Кривые поверхности/Лекции №10-15/.

Л Е К Ц И Я №10

Тема лекции

Поверхности

Содержание лекции

Задание поверхности. Определитель поверхности. Принадлежность точки поверхности. Очерк поверхности. Цилиндрическая поверхность. Коническая поверхность. Поверхность вращения. Поверхности второго порядка.

10.1 Задание поверхности.

В начертательной геометрии наибольшее распространение получил так называемый к и н е м а т и ч е с к и й с п о с о б задания поверхности. С позиций этого способа поверхность рассматривается как множество всех положений движущейся в пространетве по определенному закону линии. В качестве примера такого задания, рассмотрим задание цилиндрической и конической поверхностей.

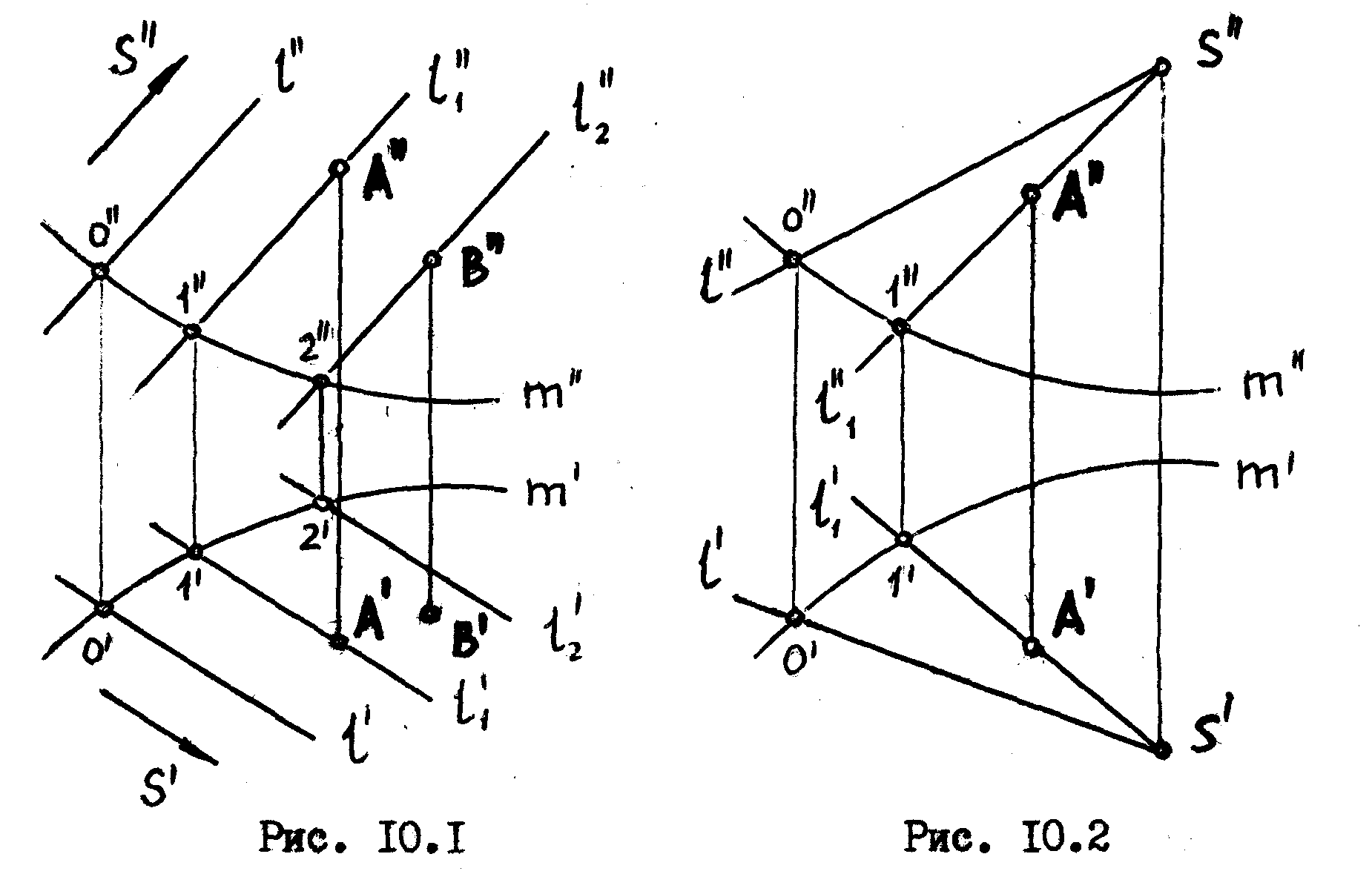
Если прямая l перемещается в пространстве так, что при своем движении она все время пересекает кривую m, и остается параллельной заданному направлtинию S , то такая прямая опишет в пространстве цилиндрическую поверхность /рис. 10.1/.

10.2

Если прямую 1 заставить перемещаться так, чтобы она при своем движении всегда проходила через точку S и пересекала кривую m, то такая прямая опишет коническую поверхность /рис.10.2/.

В обоих случаях прямая l называется о б р а з у ю щ е й , а кривая m - н а п р а в л я ю щ е й данной поверхности.

10.2 Определитель поверхности.

При кинематическом способе задания поверхности последняя будет задана, если будет возможно в любой момент движения образующей знать ее положение и форму, а это, в свою очередь, позволит однозначно ответить на вопрос - принадлежит ли та или иная точка пространства данной поверхности или нет.

Кинематический способ задания поверхности подводит нас к понятию определителя поверхности.

Определителем поверхности будем называть совокупность независимых условий, однозначно задающих поверхность.

В число условий, входящих в состав определителя, должны быть включены:

а/ геометрические фигуры /точки, линии/, с помощью которых может быть образована данная поверхность,

б/ алгоритм формирования поверхности из геометрических фигур, т.е. закон перемещения геометрических фигур, включенных в состав определителя.

Чтобы отличить эти части определителя, условимся первую часть /геометрическую/ заключать в прямые, а вторую /алгоритмическую/ - в квадратные скобки.

Тогда определитель произвольной поверхности будет иметь следующую структурную форму:

где (Г) - геометрическая часть,

[А]- алгоритмическая часть.

В качестве примера запишем определители для цилиндрической и конической поверхностей, заданных на рис.10.1 и рис.10.2 .

Для цилиндрической поверхности /рис 10.1 / определитель будет иметь вид:

Для конической поверхности /рис.10.2/:

10.3

10.3 Принадлежность точки поверхности.

Мы выше уже отметили, что поверхность может считаться заданной в том случае, если мы в состоянии однозначно ответить на вопрос - принадлежит ли заданная точка этой поверхности или нет. При определении принадлежности точки данной поверхности следует исходить из следующего правила.

Точка принадлежит поверхности в том случае, если она лежит иа

линии, принадлежащей этой поверхности.

Как видим, это правило ничем не отличается от правила, которым мы определяли принадлежность точки плоскости /см. лекцию № 3/. Следует только иметь в виду, что на плоскости в качестве такой линии мы всегда проводили прямую. При определении принадлежности точки кривой поверхности в качестве линии следует брать, если это возможно, простейшую - прямую или окружность. Если прямую или окружность на поверхности провести нельзя, следует строить более сдожную линию.

Рассмотрим примеры. Пусть нам даны фронтальные проекции точек А, принадлежащих цилиндрической /рис.10.1/ и конической /рис.10.2/ поверхностям. Требуется отыскать их горизонтальные проекции.

Для того, чтобы отыскать горизонтальные проекции точек, мы, в том и другом случаях, через точку А”, в соответствии с требованием определителя, проводим фронтальную проекцию образующей - 1”, на которой должна лежать точка А. Эта образующая пересечет направляющую m в точке I . Зная I", находии I¹, через которую проводим горизонтальную проекцию образущей – l’ . Зная положение образующей, находим горизонтальную проекцию точки – А’.

Построив точку А, принадлежащую поверхности, мы можем утверждать, что данная поверхность на чертеже задана.

Отметим, что точка В не принадлежит поверхности цилиндра /рис.10.1/, т.к. она не принадлежит образущей l2 этого цилиндра.

При рассмотрении последующих разделов настоящей лекции мы еще не раз остановимся на вопросе принадлежности точки поверхности.

10.4

10.4 Очерк поверхности.

Задание поверхности ее определителем не всегда обеспечивает наглядность чертежа, особенно необходимую при начальном изучении начертательной геометрии. Для обеспечения такой наглядности мы будем, как правило, задавать поверхность на чертеже ее очерком /очертанием/.

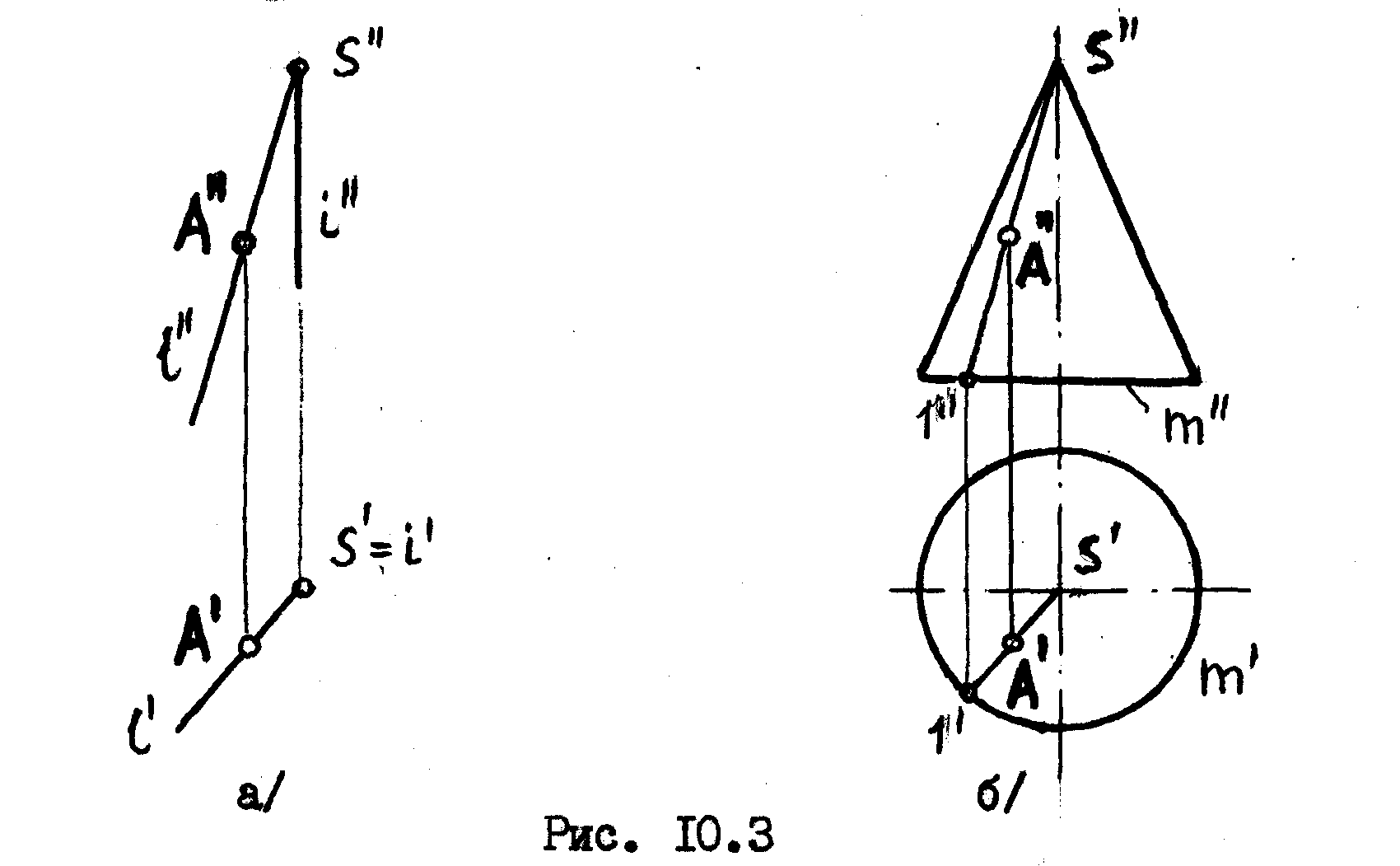
На рис 10.3а представлена круговая коническая поверхность, данная осью конуса I и образующей l, вращающейся вокруг прямой I . На рис.10.Зб та же поверхность задана своим очерком. Здесь коническая поверхность ограничена основанием конуса, заданного окружностью m . В обоих случаях точка А принадлежит поверхности конуса, т.к. она лежит на образующей l , принадлежащей поверхности конуса. Сравнивая эти два чертежа, видим , что с точки зрения наглядности изображения последний чертеж /рис.10.Зб/ имеет несомненные преимущества перед первым, хотя с точки зрения определенности задания поверхности оба чертежа равноценны, т.к. в обоих случаях мы можем построить любое положение образующей конуса и, следовательно, решать любые относящиеся к его поверхности задачи.

Полннй контур видимости конуса /рис.10.Зб/ наносят на эпюр лишь для наглядности, чтобы подчеркнуть, что за пределами этого контура нет точек, принадлежащих консу.

При этом следует помнить, что с точки зрения полноты иэображения, задание поверхности ее очерком является графически избыточным, т.е. в целях наглядности мы вносим в эти изображения элементы, которые в геометрическом смысле являются из-

10.5

лишними.

Второе замечание: задание поверхности ее очерком удобно и целесообразно лишь в том случае, когда поверхность является замкнутой, а ее ось является прямой частного положения, лучше всего - проецирующей, т.е. прямой, перпендикулярной одной из плоскостей проекций.

+ +

+

Мир поверхностей чрезвычайно широк и многообразен. Классификация их сложна и громоздка. Классификация поверхностей достаточно подробно изложена в учебнике С.А.Фролова /стр.57-92/. На лекциях мы остановимся лишь на поверхностях, нашедших наиболее широкое применение в технике. Мы рассмотрим только следующие поверхности:

а/ цилиндрические,

б/ конические,

в/ вращения,

г/ второго порядка.

10.5 Цилиндрическая поверхность.

Образование цилиндрической поверхности мы уже рассмотрели. Цилиндрическая поверхность может быть неограниченно продолжена в обе стороны по направлению ее образующих. На практике при построении изображений мы имеем дело всегда с ограниченными отрезками цилиндрической поверхности. Часть цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется, как известно из стереометрии, ц и л и н д р о м , а сами сечения - его о с н о в а н и я м и

Сечение цилиндрической поверхности плоскостью, перпендикулярной к его образующим, называется н о р м а л ь н ы м.

В зависимости от формы нормального сечения цилиндрические поверхности получают дополнительные, характеризующие их наименования . Если нормальным сечением является окружность, то цилиндр нааывают к р у г о в ы м. Только в круговой цилиндр можно вписать сферу. Поэтому, круговую цилиндрическую поверхность определяют еще как геометрическое место параллельных прямых, касательных к сфере.

Если нормальное сечение есть эллипс, цилиндр называют э л л и п т и ч е с к и м, если парабола - п а р а б о л и ч е с к и м, гипербола - г и п е р б о л и ч е с к и м.

10.6

Если нормальное сечение - геометрически неопределенная кривая, будем иметь цилиндр о б щ е г о в и д а.

Параболический и гиперболический цилиндры являются разомкнутыми, или открытыми, поверхностями.

Если за основание цилиндра принимается его нормальное сечение, цилиндр называют п р я м ы м , если за основание принято какое-либо косое сечение, то цилиндр называют н а к л о н н ы м .

Цилиндрическая поверхность, как и плоскость, может быть

п р о е ц и р у ю щ е й .

Проецирующей цилиндрической поверхностью мы будем называть такую цилиндрическую поверхность, образующие которой перпендикулярны к одной из плоскостей проекций.

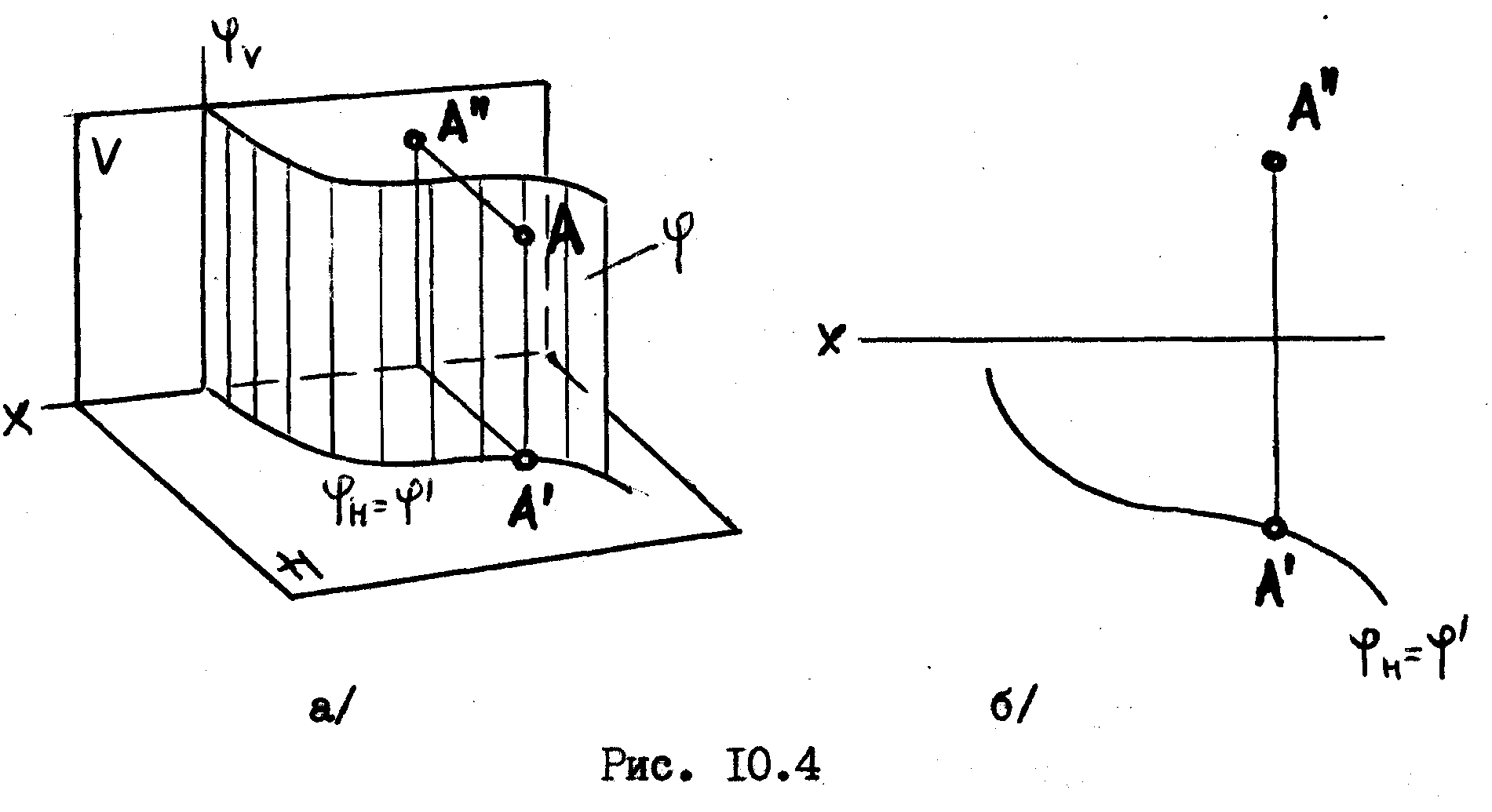
На рис.10.4а показана горизонтально-проецирующая цилиндрическая поверхность общего вида , образующие которой перпендикулярны к горизонтальной плоскости проекций Н.

На рис.10.4б показано принятое изображение такой цилиндрической поверхности на комплексном чертеже.

На рис.10.5 изображен эллиптический цилиндр, за основания которого приняты наклонные сечения, представляющие собой окружности. Такой цилиндр иногда неправильно называют наклонным круговым цилиндром.

Этот цилиндр не может быть круговым, т.к. в него нельзя вписатъ сферу.

Решим еще раз задачу на принадлежность точки поверхности. Пусть нам опять дана фронтальная проекция точки А, принадлежащей поверхности данного эллиптического цилиндра. Требуется

10.7

н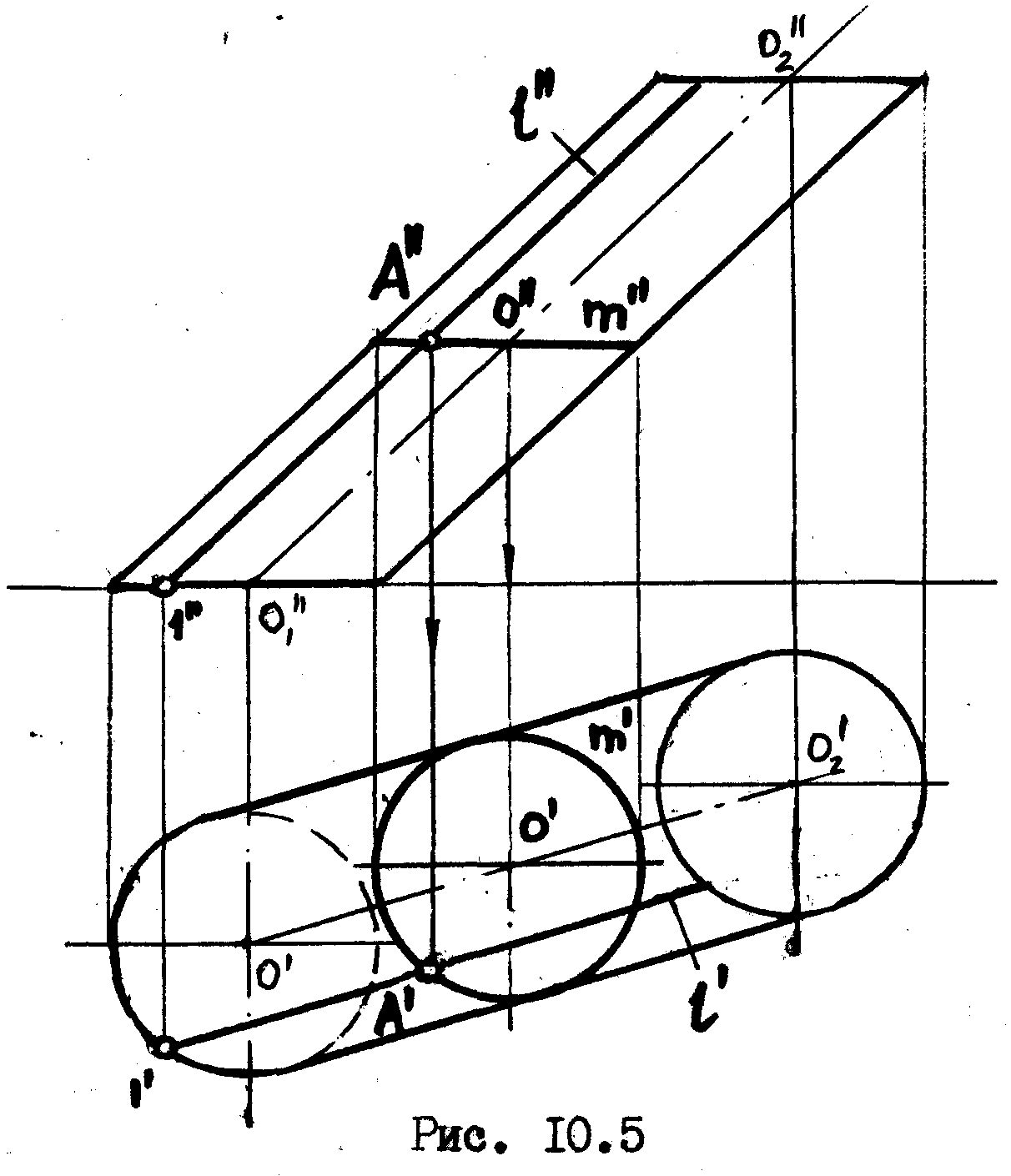 айти горизонтальную проекцию точки А.

Решить данную задачу /рис.10.5/ можно двумя путями.

1. Исходя из условия, что точка А лежит на принадлежащей цилиндру образующей 1 , которая пересекает основание цилиндра в точкв I.

2. Исходя из условия, что точка А лежит на принадлежащей цилиидру окружности m, центр которой лежит на оси цилиндра. Оба решения, естественно, дадут нам одно и то же положение горизонтальной проекции точки А.

10.6 Коническая поверхность.

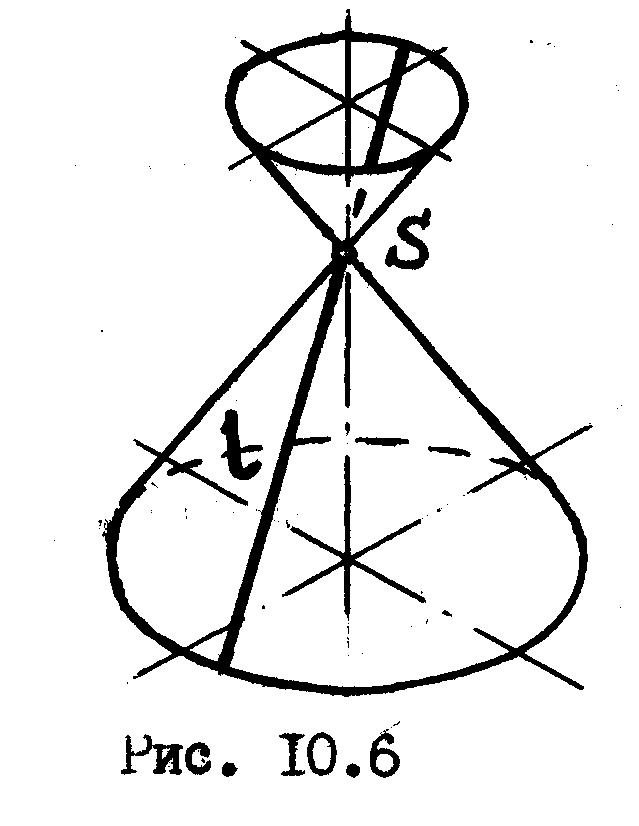О кинематическом способе задания и образования конической поверхности мы говорили выше. Коническая поверхность неограниченно простирается в обе стороны от точки S и имеет, следовательно, две полости /рис.10.6/. Часть конической поверхности, ограниченная вершиной и какой-либо плоскостью, пересекающей все образующие, называют к о н у с о м . Любое сечение коничес-

10.8

кой поверхности такой плоскостью может быть принято за

о с н о в а н и е конуса. Понятие о нормальном сечении в том виде, как мы установили его для цилиндрических поверхностей, неприменимо к коническим поверхностям, так как невозможно пересечь коническую поверхность перпендикулярно ко всем ее образующим.

Условимся называть н о р м а л ь н ы м с е ч е н и е м

к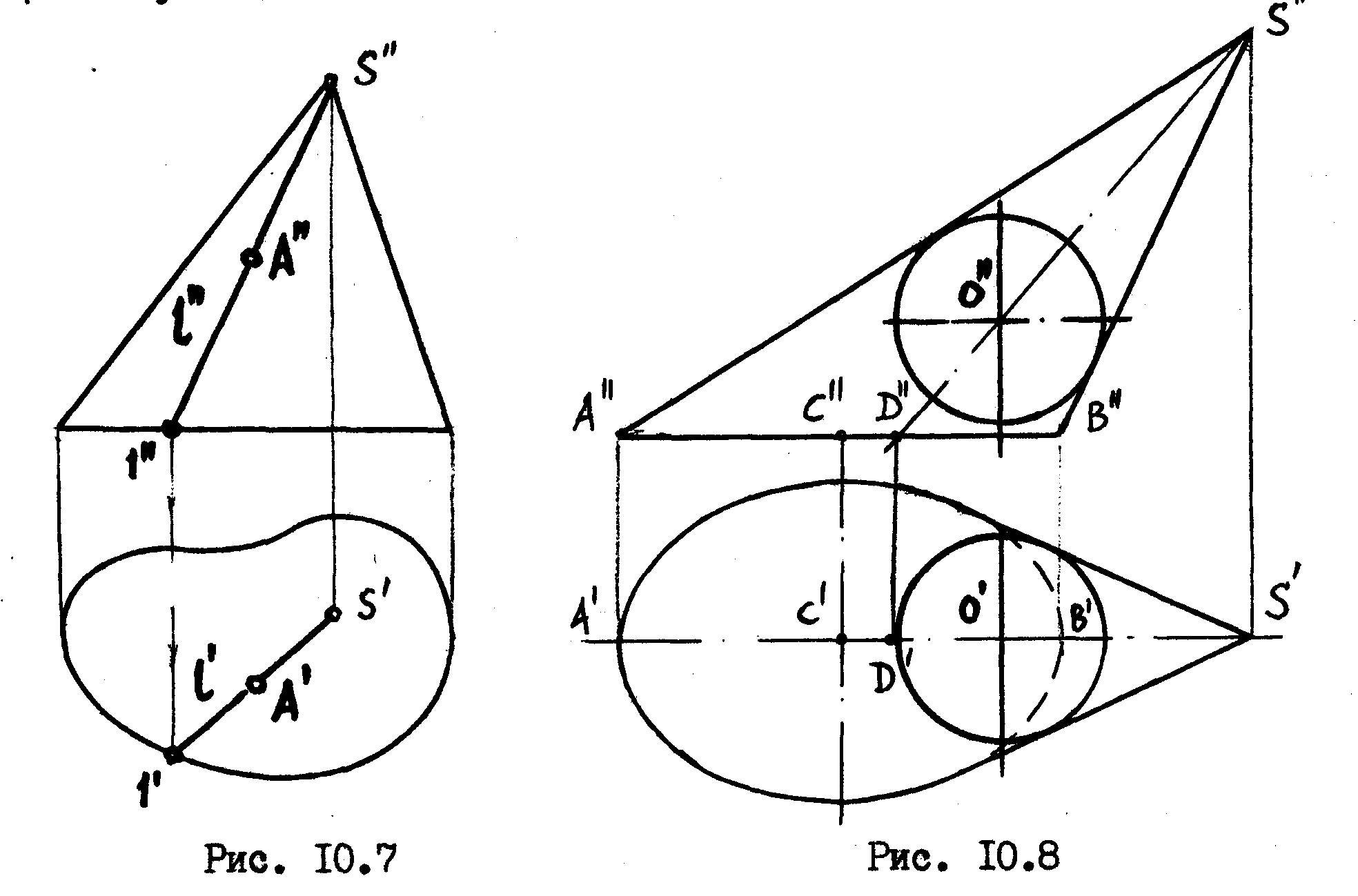 онической поверхности сечение, перпендикулярное к оси поверхности. Осью же конической поверхности будем называть линию пересечения ее плоскостей симметрии. Отсюда следует, что не все конические поверхности имеют ось, а только такие, у которых есть, по крайней мере две плоскости симметрии. На рис.10.7 приведен конус, не имеющий плоскостей симметрии и, следовательно, оси. К таким коническим поверхностям, не имеющих оси, понятие о нормальном сечении неприменимо и их назывют коническими поверхностями общего вида. Точку А, принадлежащую такому конусу, можно построить из условия ее принадлежности образующей конуса

Конические поверхности, имеющие ось, следует именовать сообразно виду нормального сечения. Если норнальное сечение коничеокой поверхности – окружность, она называется к р у г о в о й . Если принять это нормальное сечение за основание конуса, получим

п р я м о й к р у г о в о й к о н у с, у которого высота совпадает с осью и пр©ходит через центр осно-

10.9

вания /см. рис10.Зб/.

Если же за основание принять какое-либо иное сечение круговой конической поверхности, мы будем иметь наклонный круговой конус. В последнем случае /рис10.8/ основание его не может иметь форму окружности /оно будет эллипсом/, и ось конуса не будет проходить через центр основания.

В круговой конус, как прямой, так и наклонный, всегда можно вписать сферу /рис.10.8/, и наоборот, конус, описанный вокруг сферы, является круговым. Поэтому круговую коническую поверхность можно еще определить как геометрическое место касательных к сфере, исходящих из одной точки.

10.7 Поверхности вращения.

Поверхностью вращения общего вида называют поверхность, которая образуется произвольной кривой /плоской или пространственной/ при ее вращении вокруг неподвижной оси.

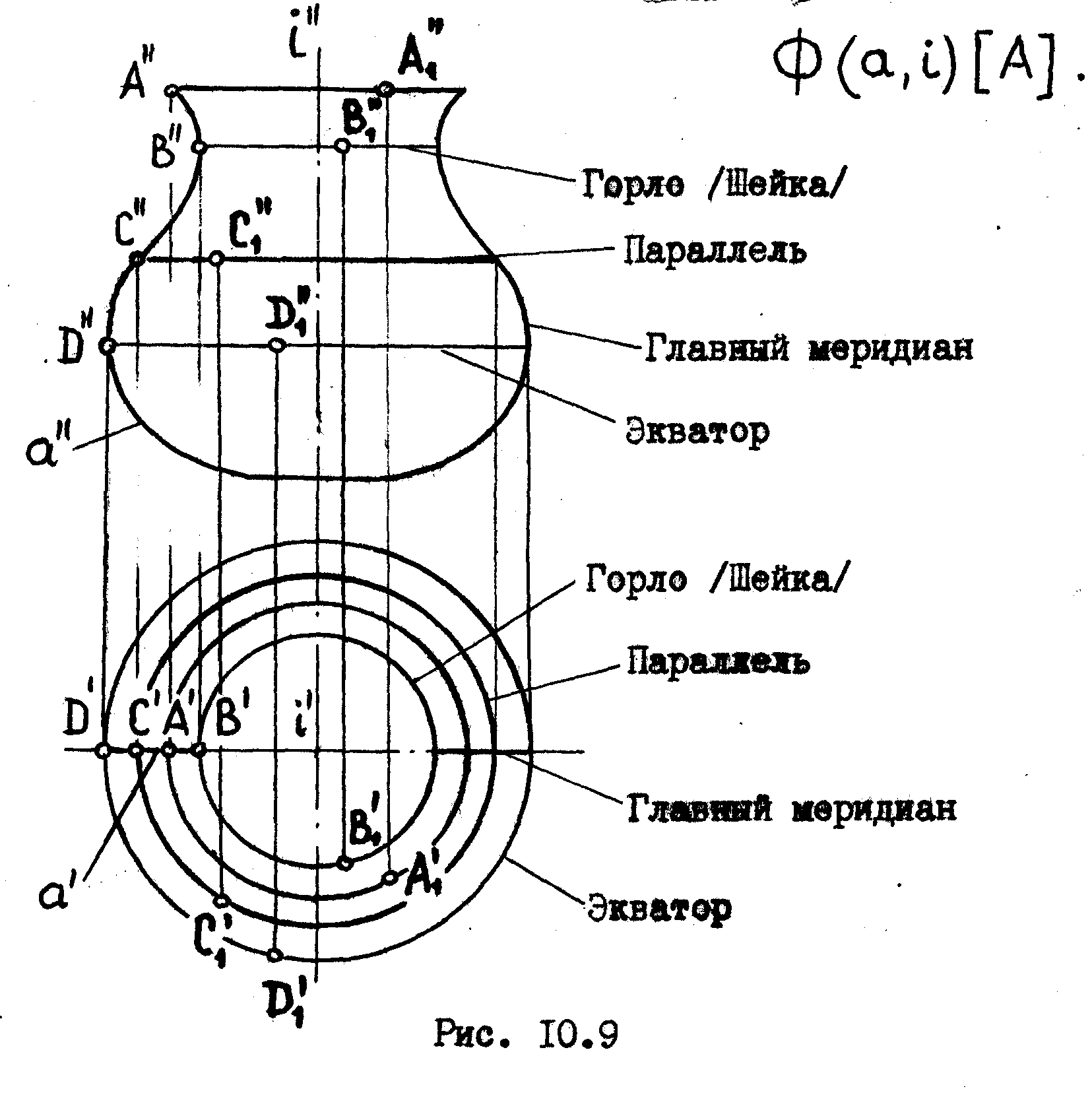
В состав определителя поверхности вращения входит образующая а, ооь вращения i , и условие [А] о том, что эта образующая вращается векруг оси i /^рис. 10.9/.

10.10

Каждая точка образующей - А,В,С,D /см.рис10.9/ при вращении вокруг оси i описывает окружность с центром на оси вращения. Эти окружности называют п а р а л л е л я м и.

Наибольшую и наименьшую параллели называют соответственно э к в а т о р о м и г о р л о м /шейкой/.

Плоскости, проходящие через ось поверхности вращения, назывют

м е р и д и о н а л ь н ы м и, а линии, по которым они пересекают поверхность -

м е р и д и а н а м и.

Меридиональную плоскость, параллельную плоскости проекций, принято называть

г л а в н о й м е р и д и о н а л ь н о й п л о с к о с т ь ю, а линию ее пересечения с

поверхностью вращения - г л а в н ы м м е р и д и а н о м.

Возьмем в качестве образующей окружность. В зависимости от взаимного расположения окружности и оси вращения можно получить различные поверхности.

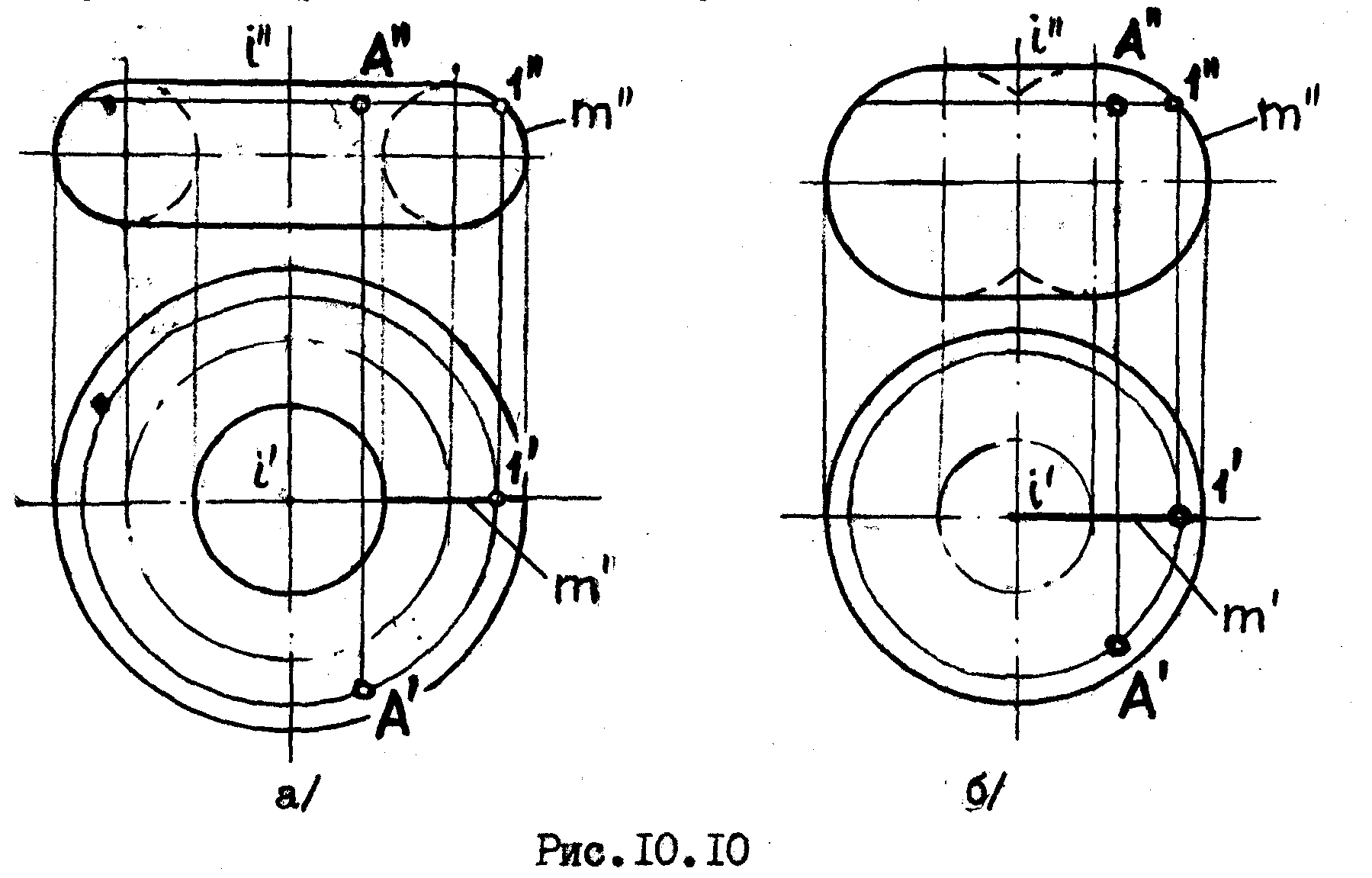Если окружность m вращать вокруг оси i , принадлежащей плоскости этой окружности и не проходящей через ее центр, мы получим поверхность, называемую т о р о м /рис10.10/.

В зависимости от взаимного расположения окружности и оси вращения поверхность тора подразделяют на:

о т к р ы т ы й тор /или кольцо/ - окружность не пересекает ось вращения /рис10.10а/ ,

з а к р ы т ы й тор- окружность первсекает ось вращения или касается ее /рис10.10б/

Точка А, принадлежащая поверхности тора, строится как точ-

10.11

ка, принадлежащая параллели этой поверхности.

Если окружность m вращается вокруг оси l , проходящей через центр этой окружности, то окружность m опишет в пространстве хорошо нам известную поверхность, называвмую с ф е р о й ./см.рис. 10.11/.

Построение точки А, принадлежащей сфере, следует выполнять как построение точки, принадлежащей окружности этой сферы /см.рис10.11/;

Следует специально оговорить,что принадлежность точки любой

произвольной поверхности вращения следует всегда определять как принадлежностъ точки параллели /окружности/ этой поверхности /см.рис. 10.9 - 10.11/.

10.8 Поверхности второго порядка.

Поверхностью n-ого порядка называют поверхность, уравнение которой есть алгебраическое уравнение степени n.

Плоскость, как известно, выражается уравнением первой степени, поэтому ее называют поверхностью первого порядка.

Поверхностью второго порядка мы будем называть поверхность, уравнение которой представляет собой уравнение 2-ой степени.

В начертательной геометрии мы не задаем поверхности их уравнениями. Этим занимается аналитическая геометрия.

Порядок поверхности в начертательной геометрии определяется максимальным количеством точек /действительных или мнимых/.

в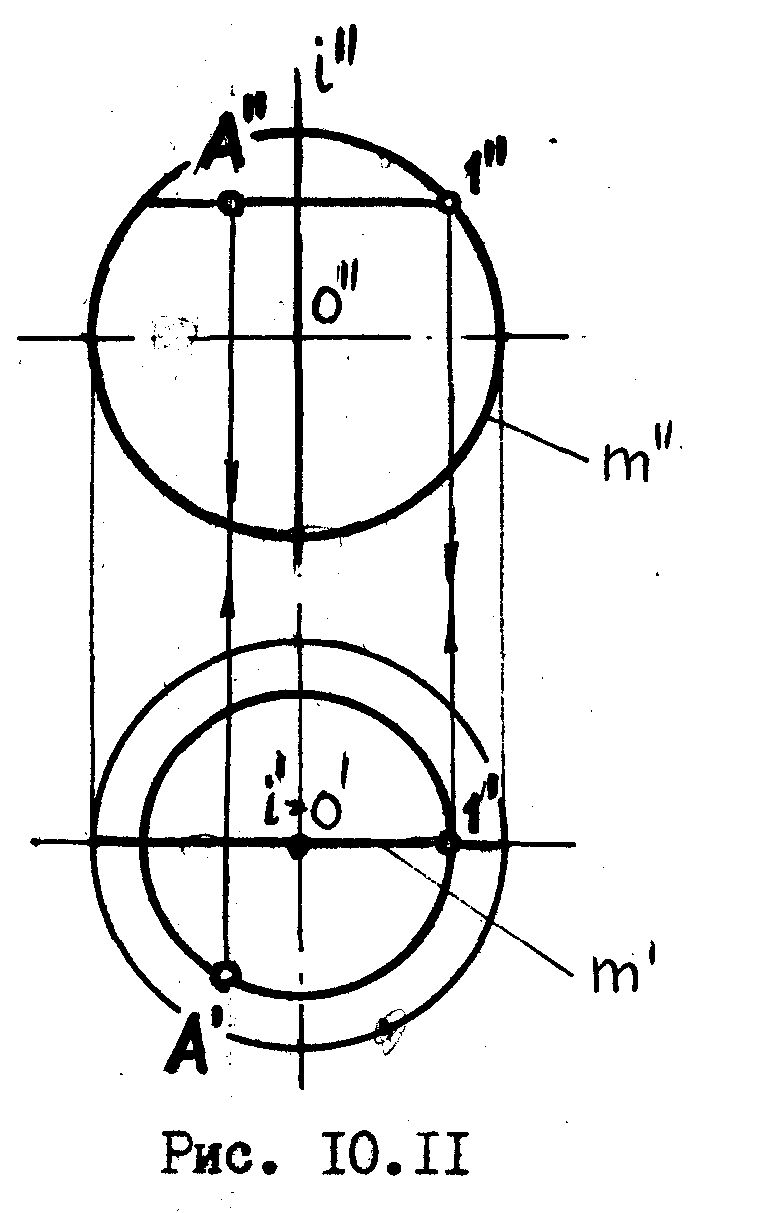 которых прямая пересекает данную поверхность. Так плоскость поверхность первого порядка, прямая может пересечь не более чем в одной точке. Сферу или круговой цилиндр, являющиеся одними из представителей поверхностей второго порядка, прямая будет пересекеть в двух точках. Тор /круговое кольцо/ есть поверхность 4-ого порядка. Эту поверхность прямая может пересечь не более чем в 4-х точках.

Порядок поверхности можно определить, руководствуясь следующим правилом.

Плоскость пересекает поверхность n-ого порядка по кривой

10.12

того же n-го порядка.

Приведем примеры этого положения. Мы уже отмечали, что плоскость является поверхностью первого порядка. Мы знаем, что плоскость пересекает другую плоскость по прямой, т.е. по линии первого порядка. Любая плоскость пересечет сферу по окружности. Сфера есть одна из поверхностей второго порядка, ее сечение - окружность есть плоская кривая второго порядка.

Если эллипс, параболу, гиперболу, т.е. известные нам кривые 2-го порядка, вращать вокруг их осей, мы получим круговые поверхности 2-ого порядка, которые будут соответственно называться эллипсоидом, параболоидом, гиперболоидом.

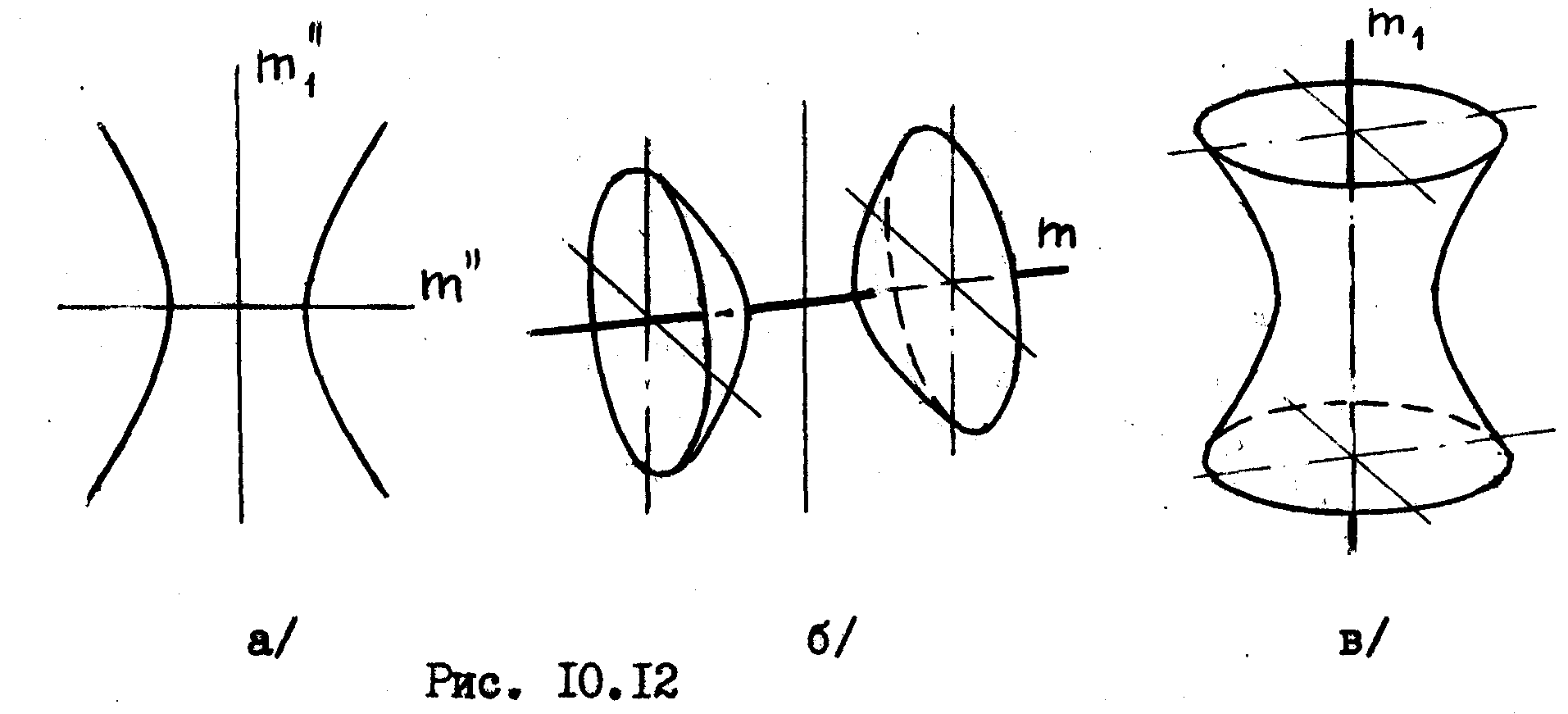
Гиперболу, кривую, состоящую из двух ветвей /рис10.12а/, мы можем вращать, как вокруг ее действительной - m, так и вокруг ее мнимой оси – m1. В первом случае мы получим двуполостной гиперболоид /рис.10.12б/, во втором - однополостный гиперболоид /рис.10.12в/.

Если поверхности вращения второго порядка подвергнуть рав-номерному сжатию или растяжению, в направлении, перпендикулярном оси поверхности, эти поверхности, из круговых, превратятся в эллиптические. Эллипсоид вращения превратится в трехосный эллипсоид, а параболоид и гиперболоид вращения преобразуются, соответственно, в эллиптический параболоид и эллиптический гиперболоид.

Перечислим все возможные поверхности 2-го порядка. Ими являются только следующие поверхности:

1/ цилиндры /круговой, эллиптический, параболический, гипэрболический/,

2/ конусн /круговой, эллептический/,

3/ эллипсоиды /вращения, трехосный/, сферу можно рассматривать как частный случай эллипсоида, все осм ко-

10.13

торого равны,

4/ параболоиды /вращения, эдлиптический и гиперболический/,

5/ однополостные гиперболоиды /вращешя и эллиптический/,

6/ двуполостные гиперболоиды /вращения и эллиптический/.

За исключением трех поверхностей: гиперболического и параболического цилиндров и гиперболического параболоида, все остальные могут пересекаться плоскостью по окружности. Таким образом, на всех поверхностях второго порядка, кроме трех указанных, можно расположить бесчисленное множество окружностей.

Материал лекции /не полностюо/ изложен в учебнике С.А.Фролова /изд.1978 г./ на стр. 51-57 , 86-90.

11.3

На рис. 11.2 приведен пример сечения поверхности вращения горизонтально-проецирующей плоскостью . В этом случае уже горизонтальная проекция сечения будет представлять собой прямую линию, совпадающей с горизонтальным следом плоскости . Зная, что эта линия принадлежит поверхности, можно легко построить ее фронтальную проекцию. Построение начинаем с точек 1 и 2, принадлежащих окружности основания. Построение точзк 3,4 является типичным для построения промежуточных точек. Построение точки 5 иллюстрирует определение верхней точки сечения. Точка 6 - точка сечения, принадлежащая главному меридиану, в которой на фронтальной проекции кривая фигуры сечения из видимой переходит в невидимую.

Отметить, что переход видимой ветви кривой сечения в невидимую, всегда происходит в точке, лежащей на очерке поверхности.

11.2 Конические сечения.

Круговой цилиндр можно рассечь по эллипсу и по прямым линиям. Эллипс получится в том случае, если секущая плоскость будет наклонной по отношению к оси цилиндра. Если же секущая плоскость будет, параплельна оси цилиндра она рассечет, последний по прямым линиям - его образующим.

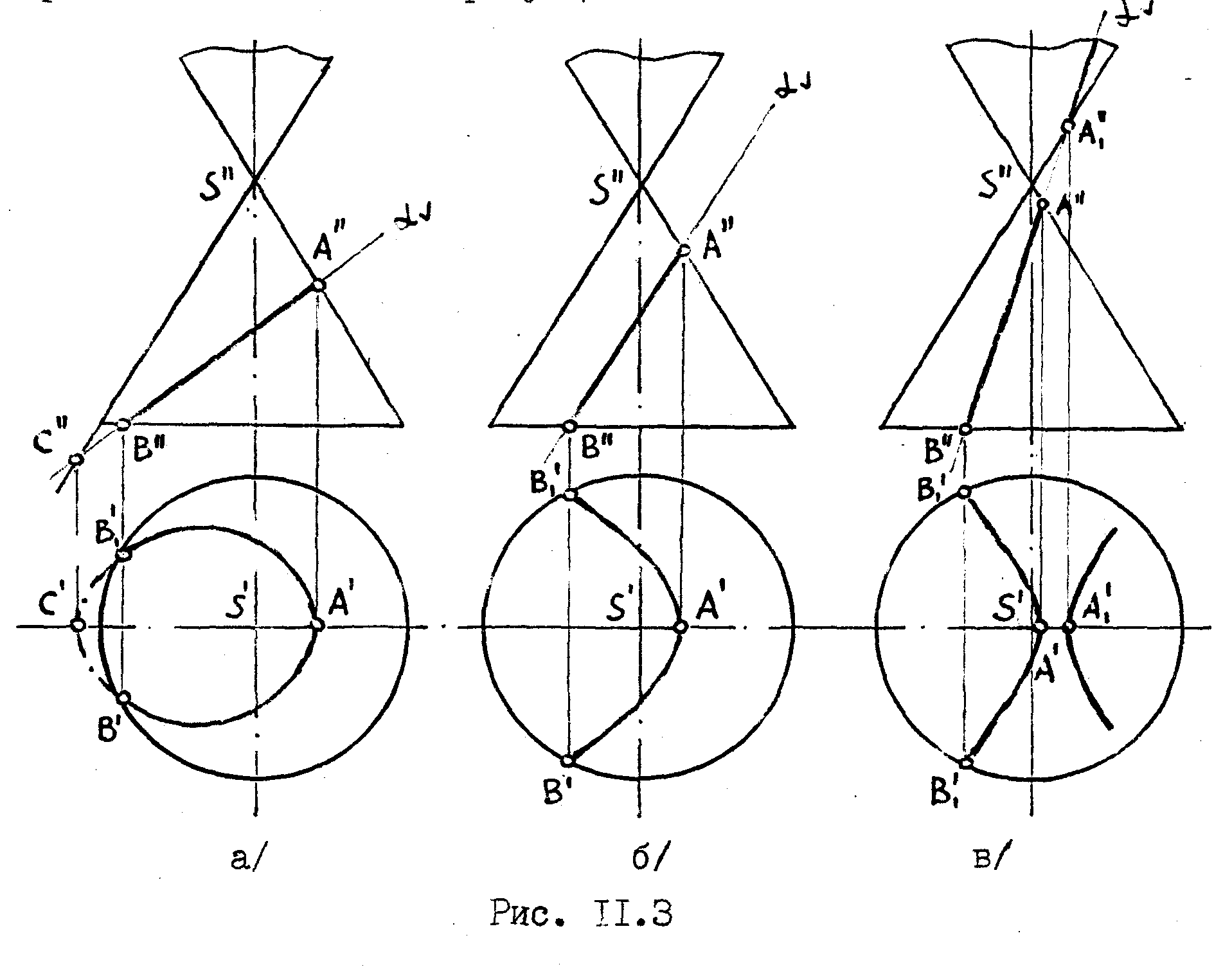
11.4

Более разнообразны сечения кругового конуса. Прежде всего, надо отметить тот единственный случай, когда конус пересекается плоскостью по двум прямым линиям - по образующим. Это иметь место лишь при условии, если секущая плоскость проходит через вершину конуса.

Если же секущая плоскость не проходит через вершину конуса, то в сечении получаются кривые линии, причем они могут быть только трех видов: эллипсы, параболы и гиперболы. Все эти кривые, как известно, являются кривыми второго порядка.

Э л л и п с получается в сечении конуса наклонной плоскостью, не параллельной ни одной из его образующих, т.е. пересекающей все образующие конуса /или их продолжения/,/рис. 11.3 а/.

П а р а б о л а получается в том случае, если секущая плоскость параллельна какой-либо о д н о й образующей /рис.11.Зб/,

Г и п е р б о л а получается при условии, если секущая плоскость параллельна д в у м образующим. В частности, это будет иметь место тогда, когда секущая плоскость параллельна оси конуса /рис.11.Зв/.

Ясно, что в обоих последних случаях кривая сечения должна быть разомкнутой, так как плоскость пересекает не все образующие

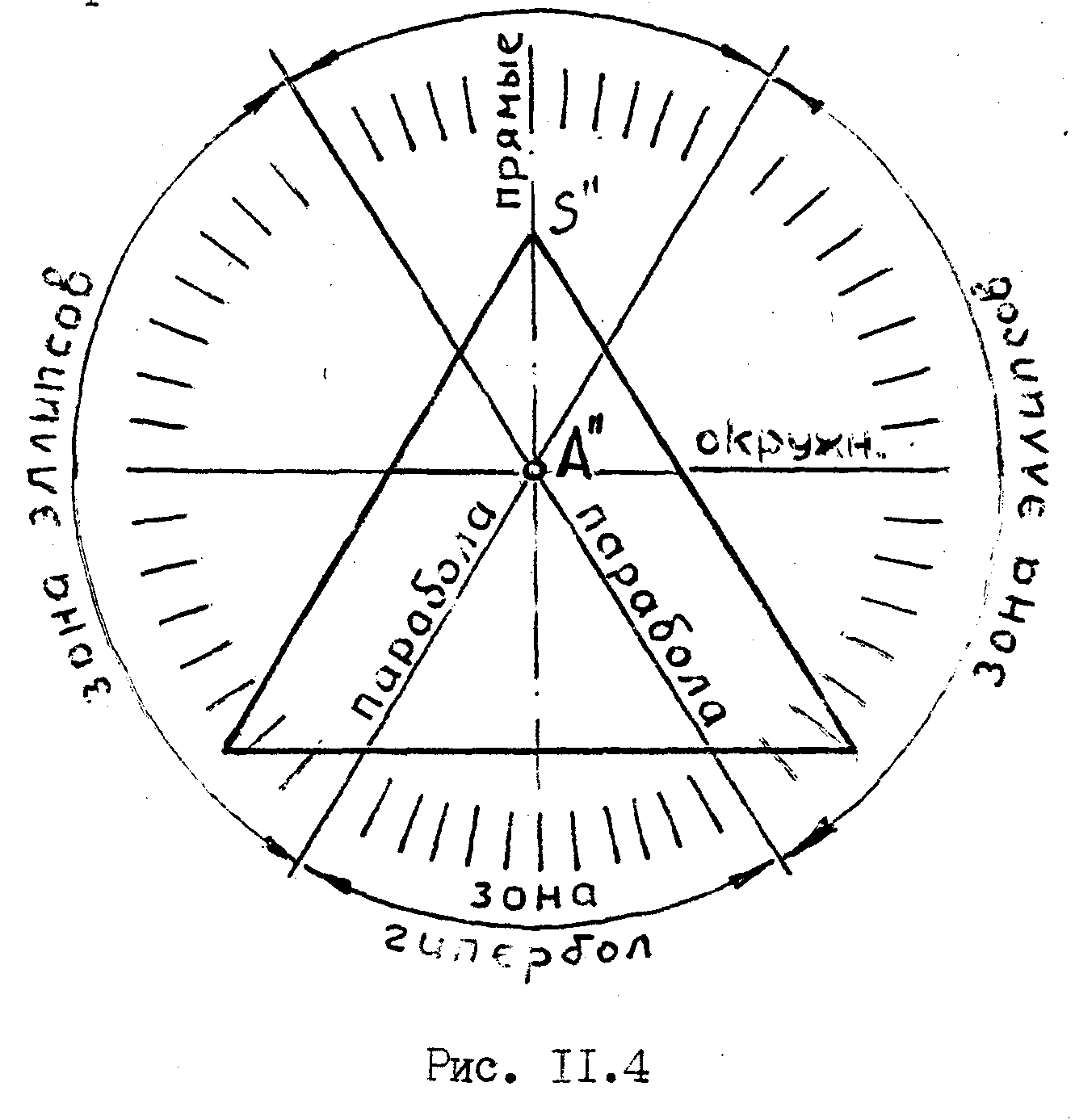
Подойдем к рассмотрению конических сечений несколько с иной стороны /рис.11.4/.

.

11.5

Если секущую фронтально-проецирующую плоскость провести через точку А, лежащую на оси конуса, а затем начать придавать ей новые положения,путем вращения около оси, проходящей через А и перпендикулярной плоскости V , то в каждом своем новом положении эта плоскость будет рассекать конус по той или иной кривой.

Из рис. 11.4 видно, что положения секущей плоскости, дающей в сечении параболы, являются граничными, отделяющими зону сечений по эллипсу от зоны сечений по гиперболе.

В том случае, когда секущая плоскость пройдет через вершину конуса, сечение по гиперболе распадется на две прямые, а в том случае, когда эта плоскость окажется перпендикулярной оси конуса, в сечении получится окружность.

11.3 Пересечение прямой с поверхностью. Алгоритм определения точек пересечения прямой с поверхностью.

Рассмотрим вначале общий случай. Под общим будем понимать случай, при котором прямая занимает общее положение, как относительно плоскостей проекций, так и относительно поверхности.

Алгоритм решения задачи на отыскание точек пересечения прямой с поверхностью по своей сути ничем не отличается от алгоритма решения задачи на отыскание точки пересечения прямой с плоскостью. Последний алгоритм был изложен на лекции №4.

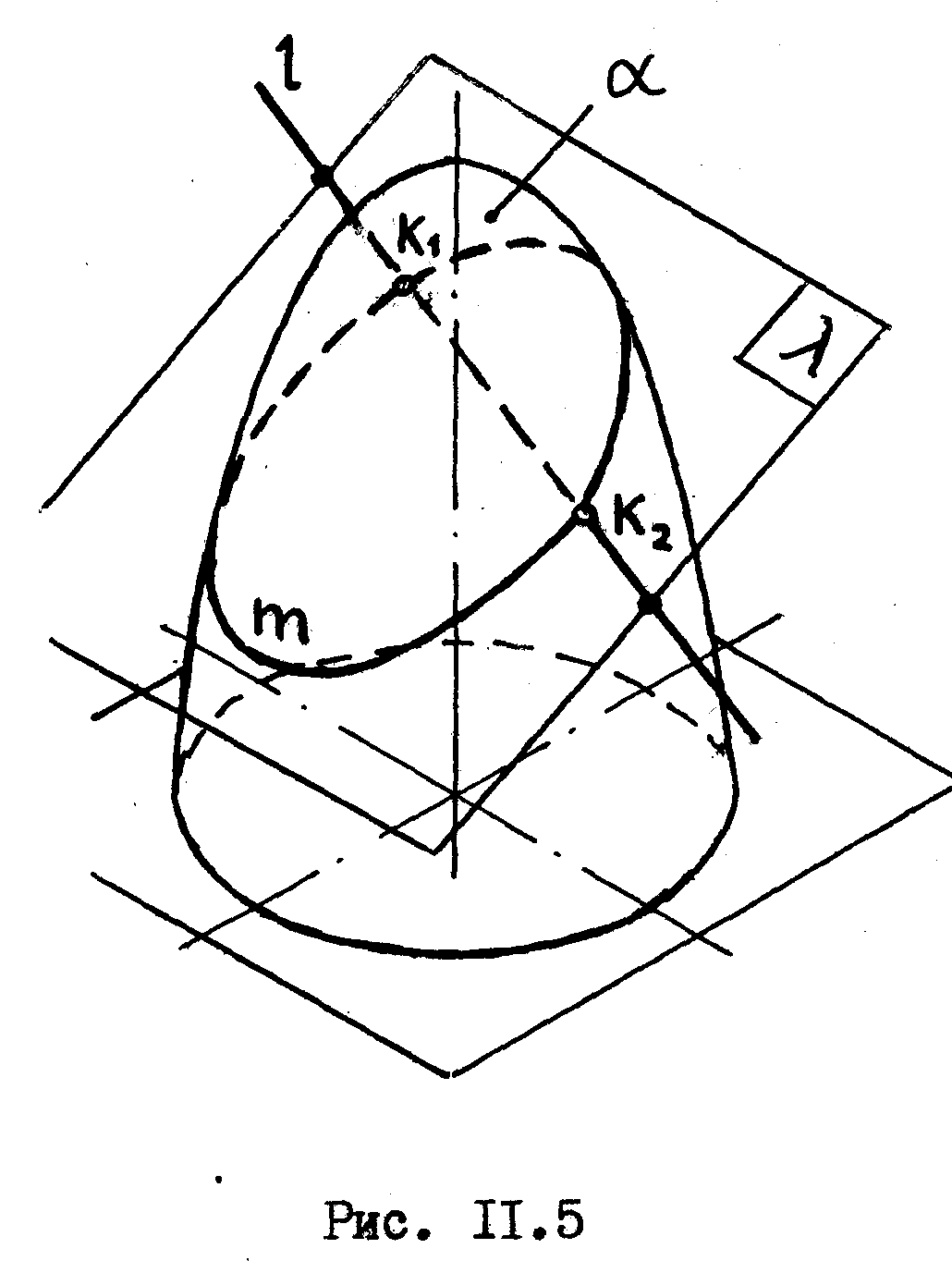
Алгоритм задачи на пересечение прямой с поверхностью /рис.11.5/ состоит в следущем.

Для того, чтобы отыскать точки пересечения прямой с поверхностью необходимо:

1/заключить прямую во вспомогательную секущую плоскость,

2/ построить фигуру сечения поверхности данной плоскостью,

3/ построить точки пересечения прямой с поверхностью, как точки пересечения прямой с найденой линией сечения,

11.6

4/ выделить видимые и невидимые участки прямой.

Настоящая задача является более сложной, чем задача на определение точки пересечения прямой с плоскостью. Это усложнение состоит в том, что если в первой задаче фигурой сечения была прямая, то в настоящей задаче фигурой сечения, как правило, будет кривая линия, построение которой будет более сложным делом, чем построение прямой. Но и фигура сечения может видоизменяться в зависимости от выбора положения секущей плоскости, проходящей через прямую. Ведь таких плоскостей можно провести сколь угодно много. Возникает дополнительная задача - так выбрать положение секущей плоскости, чтобы фигура сечения оказалась простейшей, что, в свою очередь, приведет к упрощению решения всей задачи.

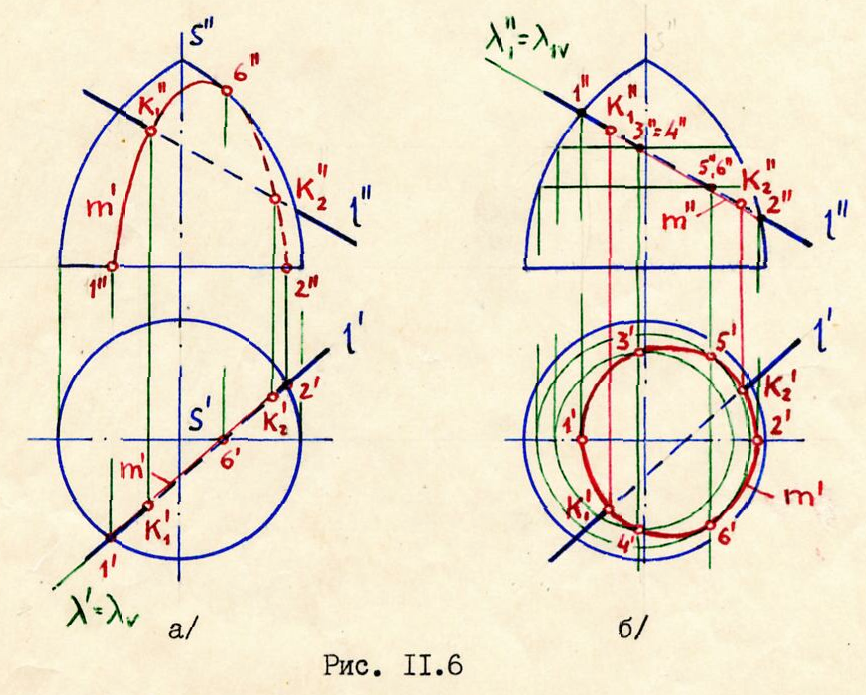Рассмотрим решение типовой задачи на комплексном чертеже. Необходимо найти точки пересечения прямой l с поверхностью вращения /рис.11,6/. На указанном чертеже приведены два варианта решения этой задачи.

На рис11.6а через прямую l проведена горизонтально-проецирующая плоскость /прямая 1 заключена в плоскость /. Линия сечения m строится так, как было показано на настоящей лекции /рис.11.2/. По этой причине нет необходимости строить эту кривую вновь, достаточно нанести ее приближенно.

11.7

Построив таким образом фигуру сечения m находим точки пересечения прямой 1 с поверхностью и устанавливаем видимость прямой.

На рис. 11.6б повторено решение той же задачи, но в этом случае прямая l заключается во фронтально-проецирующую плоскость 1 . Построив сечение поверхности этой плоскостью - кривую m, также находим точки пересечения прямой с поверхностью точки К1 и К₂. Оба приведенные решения /рис.11.6а,б/ с точки зрения объема графической работы являются равноценными. Найти другое положение секущей плоскости, при котором получилось бы более простое решение, чем полученные, в данной задаче не удается.

Содержание лекции №11 изложено в учебнике С.А.Фролова на стр. 127-131, 152.

12.1

Л Е К Ц И Я № 12

Тема лекции

Пересечение прямой с поверхностью.

Содержание лекции.

Пересечение прямой с цилиндрической и конической поверхностями. Пересечение прямой со сферой. Частные случаи пересечения прямой с поверхностьо вращения.

12.1 Пересечение прямой с цилиндрической поверхностью.

При решении задачи на отыскание точек пересечения прямой с поверхностью применение в качестве посредников

п р о е ц и р у ю щ и х плоскостей хотя и может привести к цели, но нередко дает крайне сложные в графическом отношении и неточные решения.

В некоторых задачах решение может быть значительно упрощено, если в качестве вспомогательной секущей плоскости брать не проецирующую, а соответсвующим образом выбранную плоскость общего положения. Этот прием применяется при решении рассматриваемых задач на пересечение прямой с цилиндрической и конической поверхностями.

Пусть требуется найти точки встречи прямой l с поверхностью эллиптического цилиндра /рис.12.1/. Какую, бы проецирующую плоскость мы не провели через прямую l , одна из проекций сечения будет эллипсом. Можно, конечно, построить этот эллипс и найти его пересечение с данной прямой, но такое решение нецелесообразно.

В подобных случаях выбор вспомогательной секущей плоскости, проводимой через данную прямую, производится с таким расчетом, чтобы получить в сечении п р о с т ы е и у д о б н ы е д л я

п о с т р о е н и я л и н и и, например прямые или окружности.

На рис. 12.1 а и б через прямую l проведена плоскость, параллельная образующим цилиндра. Ясно, что такая плоскость должна рассечь поверхность цилиндра по прямым линиям /по образующим/, построение которых не представляет труда. Чтобы провести эту плоскость на эпюре, возьмем на прямой l две произвольные точки А и В и проведем через них прямые m и n, параллельные образующим цилиндра. Две параллельные прямые m и n определяют

12.2

т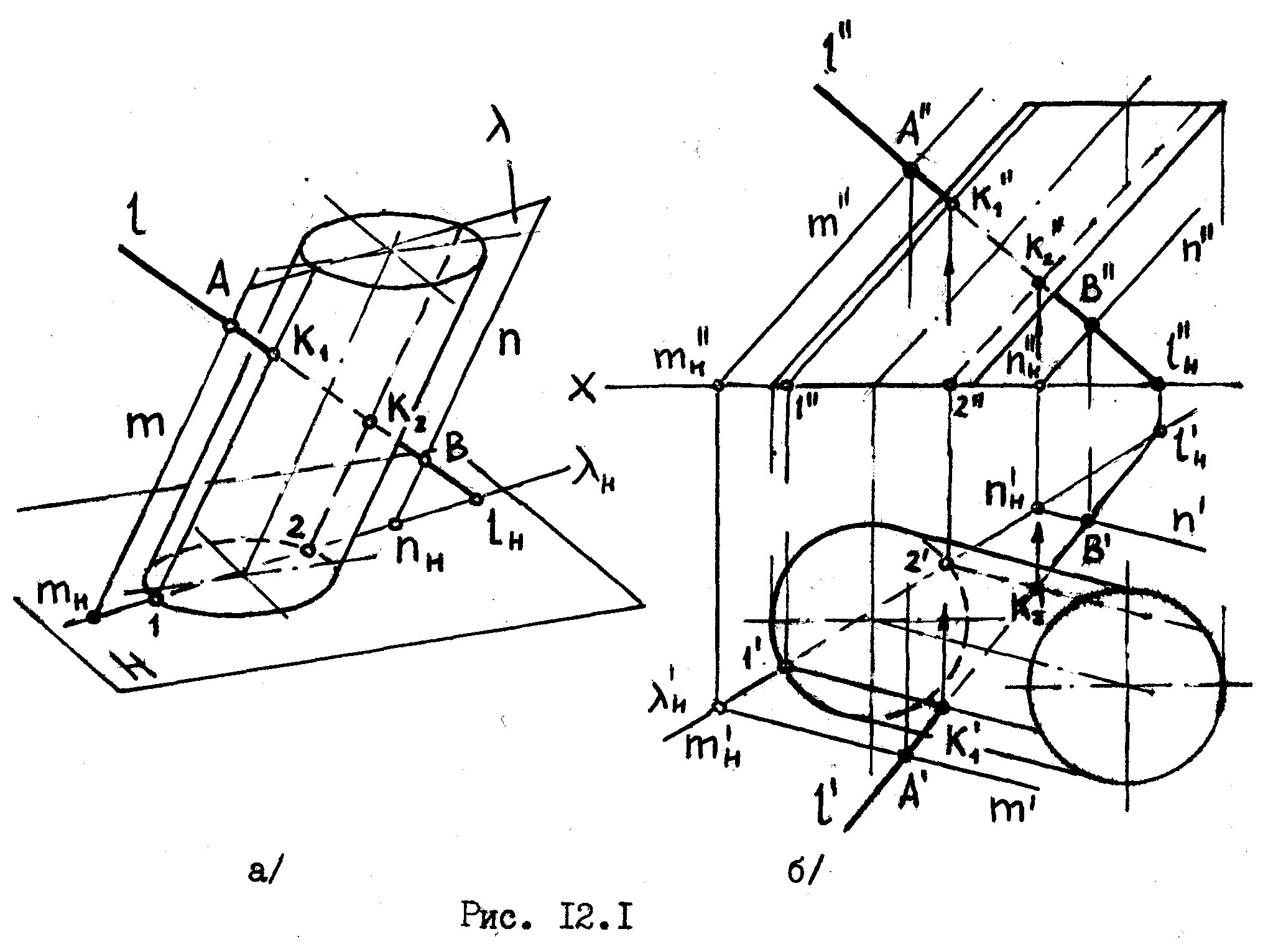 ребуемую плоскость. Найдем теперь линию пересечения этой плоскости с плоскостью основания цилиндра, т.е. с плоскостью Н.

Прямая m пересечет плоскость Н в точке, mn а прямая n , в точке nn. Соединяя точки mn и nn получаем линию пересечения нашей плоскости с плоскостью Н, т.е. ее горизонтальный след. Эта прямая пересекает основание цилиндра, находящееся также в плоскости Н, в точках 1 и 2. Через эти точки и пройдут горизонтальные проекции образующих, по которым плоскость рассекает поверхность цилиндра. В пересечении их с 1 получены точки , по которым построены затем фронтальные проекции .

Если горизонтальный след 1_Н данной прямой l находится в пределах чертежа, то вместо двух вспомогательных прямых m и n достаточно провести одну из них. Тогда секущая плоскость будет определяться двумя пересекающимися прямыми - l и m или 1 и n, а след плоскости пройдет через следы этих прямых, т.е. через lн и mн /или nн /.

12. 3

12.2 Пересечение прямой с конусом.

Если вместо цилиндра взять конус, то вспомогательную секущую плоскость придется выбрать уже по другим соображениям /см. рис.12.2/. Дейетвительно, плоскость может рассекать коническую поверхность по прямым линиям /по образующим/ только в том случае, если она проходит через вершину конуса. Поэтому вспомогательную секущую плоскость через прямую l следует провести так, чтобы она проходила еще и через вершину конуса. Для этого вершину конуса соединяем прямой SА с какой либо точкой А, взятой на прямой 1 /или с двумя точками этой прямой/. Две пересекающиеся прямые /SА и l/ и определяют требуемую вспомогательную плоскость . Далее строится линия пересечения этой плоскости с плоскостью основания конуса, являющейся в нашей задаче фронтально-проецирущей шюскостыо оС

Прямая l пересекает плоскость в точке В, а прямая SА в точке С. Прямая ВС будет прямой, по которой секущая плоскость пересекает плоскость основания конуса . Следовательно, вспомогательная секущая плоскость пересекает основание ко-

12.4

нуса в точках 1 и 2, которые дают возможность провести образующие.S1 и S2, т.е. прямые по которым плоскость рассекает поверхность конуса. В пересечении их с l находим иcкомые точки пересечения l с поверхностью конуса – К1 и К₂.

12.3 Пересечение прямой со сферой.

Настоящая задача является примером использования методов преобразования чертежа при решении задач на пересечение прямой с поверхностью. В данной задаче в качестве вспомогательной можно взять любую проецирующую плоскость, так как в сечении сферы любой плоскостью всегда получается окружность. В нашем примере /рис.12.3/ взята горизонтально-проецирующая плоскость . Окружность, что получится в сечении сферы этой плоскостью, спроецируется на плоскость V в виде эллипса

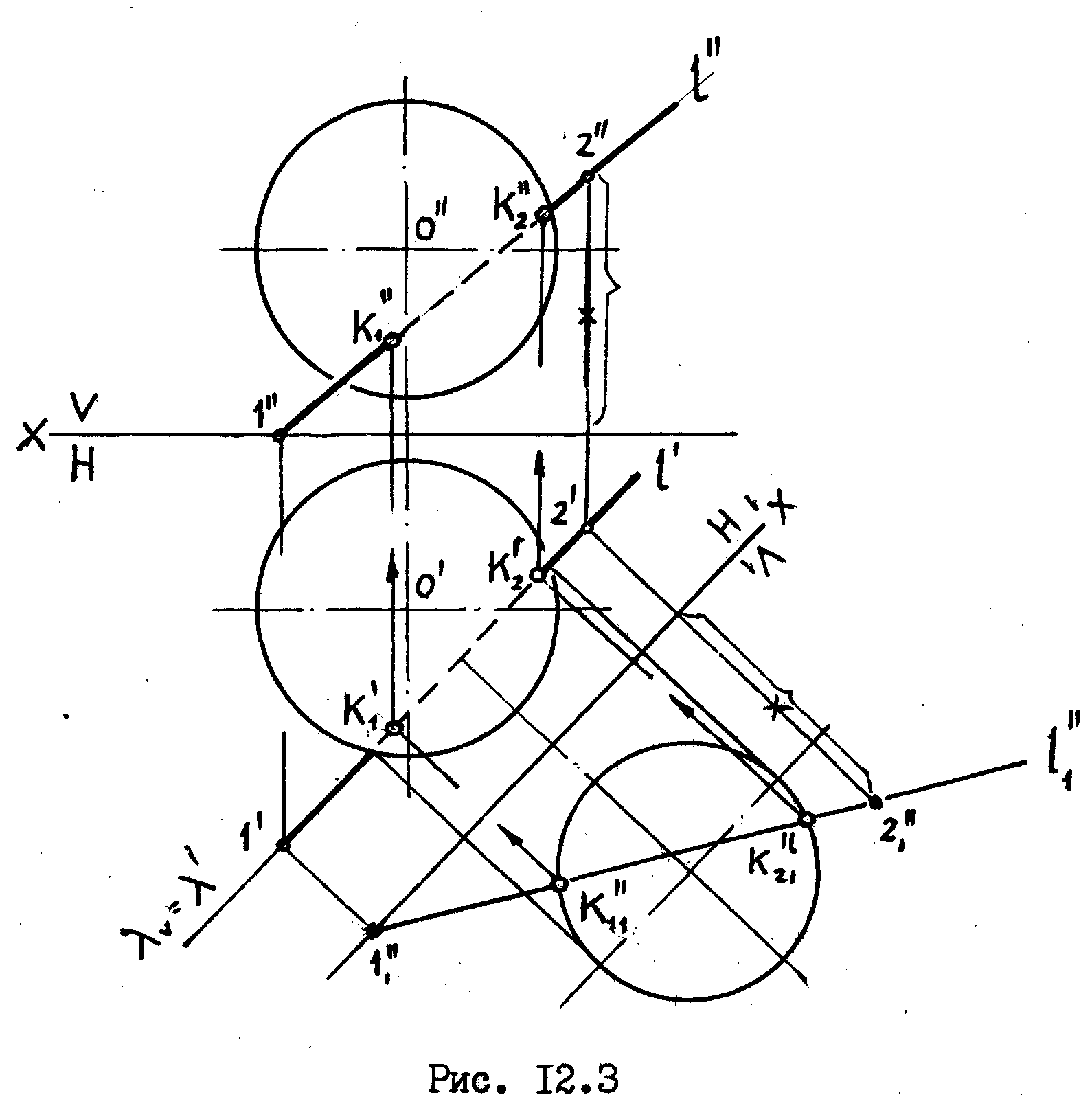
Чтобы избежать сложности построения этой кривой, целесообразно сделать замену фронтальной плоскости проекций V на V1. На плоскость V1 окружность сечения спроецируется в натуральную величину. В системе определяем проекции точек пересечения -

12.5

К11 и К21 зная которые находим проекции этих точек в заданной

сиетеме плоскостей проекций , а затем .

12.4 Частные случаи пересечения прямой с поверхностью вращения.

12.4.1 Прямая, перпендикулярная оси поверхности.

Обычно поверхность вращения на чертеже задается таким образом, что ее ось располагается перпендикулярно одной из плоскостей проекций. Поэтому прямая, перпендикулярная оси поверхности, оказывается одновременно и параллельной одной из плоскостей проекций.

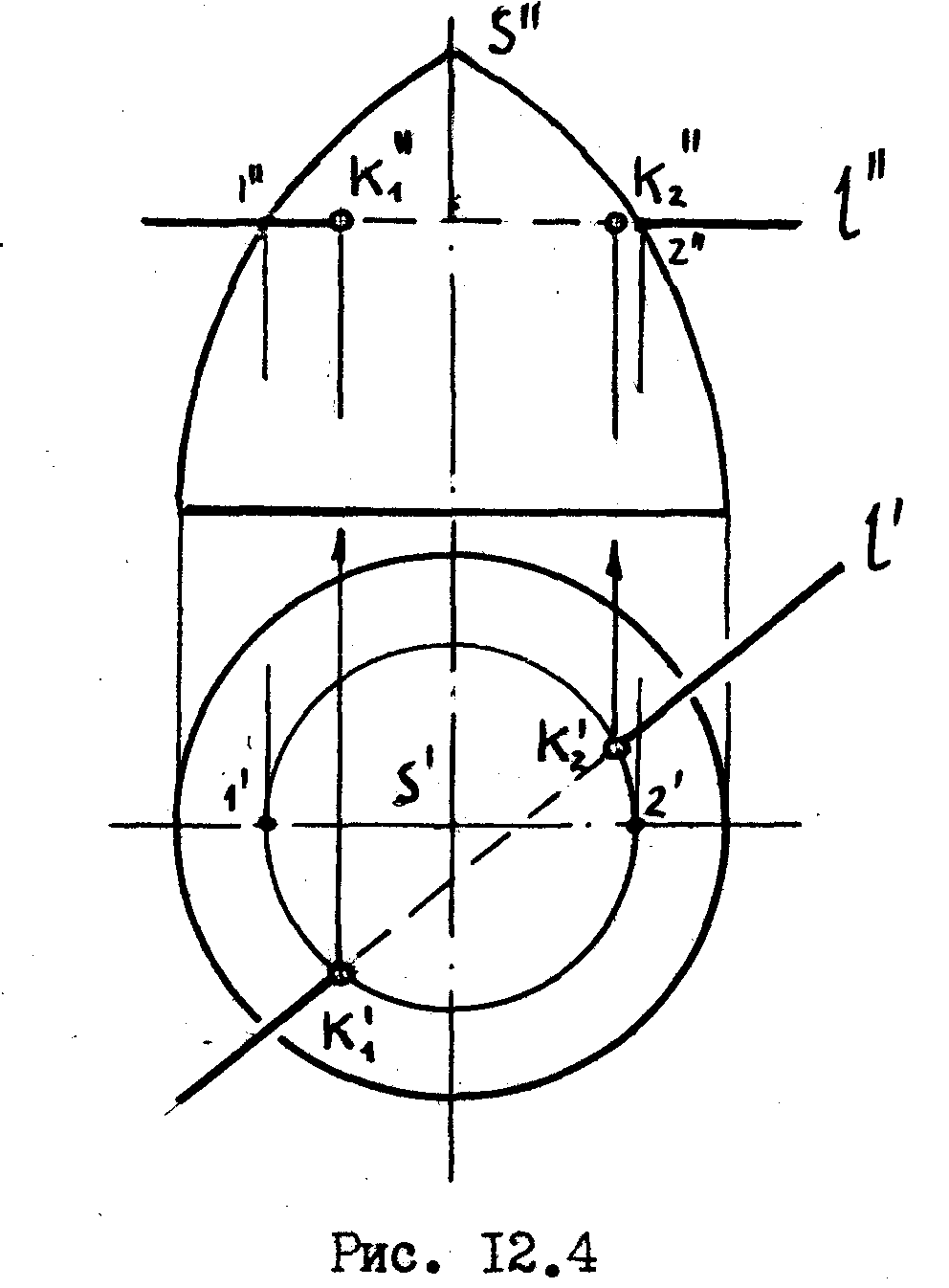Рассмотрим пример, приведенный на рис. 12.4. Как и в любом другом, в данном случае через прямую можно провести две проецирующие плоскости. Сравнивая сложность и трудоемкость получаемых решений, предпочтение следует отдать фронтально-проецирующей /горизонтальной/ плоскости, которая рассечет поверхность по простейшей кривой - окружности. Эта окружность будет проецироваться на плоскость Н в натуральную величину.

В пересечении прямой I с этой ок^жностью получаем искоше точки пересечения прямой с поверхностью- К,и Кг.»,

12.6

12.4.2 Прямая пересекает ось поверхности.

При решении такой задачи /рис.12.5/ с целью его упрощения следует также прибегнуть к преобразованию чертежа. Прямую, вместе с поверхностью вращаем около оси поверхности до положения, при котором прямая станет фронталью. Очерки поверхности при этом не изменятся. Проводим через прямую, занявшую новое положение, секущую фронтальную плоскость , которая рассечет нашу поверхность по главному меридиану.

Следовательно, очерк поверхности на плоскости V ,будет представлять собой фигуру сечения этой поверхности плоскостью . Определяем точки пересечения К11 и К₂₁. Затем обратным вращением определяем искомые проекции точек пересечения и .

Содержание лекции №12 изложено в учебнике С.А.Фролова на стр.153-154

13.1

Л Е К Ц И Я № 13

Тема лекции.

Взаимное пересечение поверхностей. Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей.

Содержание лекции.

Поверхности-посредники. Метод вспомогательных секущих плоскостей. Пересечение поверхности с плоскостью общего положения. Взаимное пересечение поверхностей. Особенности пересечения поверхностей второго порядка. Теорема Монжа.

13.1. Поверхности-посредники.

В задачах на построение линии пересечения заданных поверхностей пользуются вспомогательными поверхностями-посредниками, которые каждую из заданных поверхностей пересекают по какой-то линии. Пересечение этих линий, в свою очередь, дает нам точки, общие для обеих поверхностей, т.е. точки, принадлежащие линии пересечения этих поверхностей. Для упрощения задачи выбирают такие поверхности-посредники, которые пересекали бы заданные поверхности по наиболее простым для построения линиям прямым или окружностям.

Поэтому, в качестве вспомогательных поверхностей-посредников пользуются, либо вспомогательными секущими плоскостями, либо вспомогательными секущими сферами.

На настоящей лекции мы познакомимся с методом вспомогательных секущих плоскостей, на следующей - с методом вспомогательных секущих сфер.

13.2. Метод вспомогатвльных секущих плоскостей.

Этот метод нам уже знаком. Мы использовали его при решении задачи на отыскание линии пересечения двух заданных плоскостей /см. лекцию №4/. Зная, что линией пересечения, двух плоскостей является прямая, для ее отыскания нам было достаточно узнать положение двух ее точек. Пересекая заданные плоскости вспомогательной плоскостью-посредником, мы находили две прямые, по которым вспомогательная плоскость пересекала заданные плоскости. Точка пересечения этих прямых давала нам точку, принадлежащую одновременно двум заданным плоскостям, т.е.

13.2

точку, принадлежащую их линии пересечения. Вторая вспомогательная секущая плоскость, таким же образом, давала вторую точку искомой прямой.

Аналогичная идея лежит в основе решения рассматриваемой задачи на отыскание линии пересечения двух кривых поверхностей. Пересекая, обе поверхности плоскоетью-посредником мы найдем, линии пересечения этой плоскости с той и другой поверхностью. Поскольку эти линии лежат в одной плоскости, они будут пересекаться между собой, и точки их пересечения будут общими точками для обеих поверхностей, т.е. точками их линии пересечения.

Линией пересечения двух кривых поверхностей, в общем случае, является пространственная кривая. Для построения этой кривой потребуется уже не две, а значительно большее количество точек. Для отыскания этих точек необходимо будет провести не две, а несколько секущих плоскостей.

Выбор той или другой вспомогательной плоскости производится с таким расчетом, чтобы в пересечении ее с каждой из данных поверхностей получались простые и удобные для вычеркивания линии-прямые, либо окружности.

13.3 Пересечение поверхности с плоскостью общего положения.

В качестве примера рассмотрим задачу на построение линии пересечения поверхности вращения с плоскостью общего положения. Эта задача, по сравнению с задачей общего вида, будет более простой, т.к. одна из заданных поверхностей является простейшей плоскостью.

Задача.

Построить линию пересечения поверхности вращения с плоскостью общего положения . /рис. 13.1/.

Решение

В данной задаче плоскостью-посредником, дающей наиболее простое решение, будет горизонтальная плоскость. Она будет пересекать наши поверхности по простейшим линиям: поверхность по окружности, а плоскость - по прямой /по горизонтали/. В качестве первой такой плоскости возьмем плоскость проекций Н, которая пересечет поверхность по окружности. Основания m, а плоскость - по ее горизонтальному следу . Пересечение этих линий, лежащих в одной плоскости, дают нам искомые

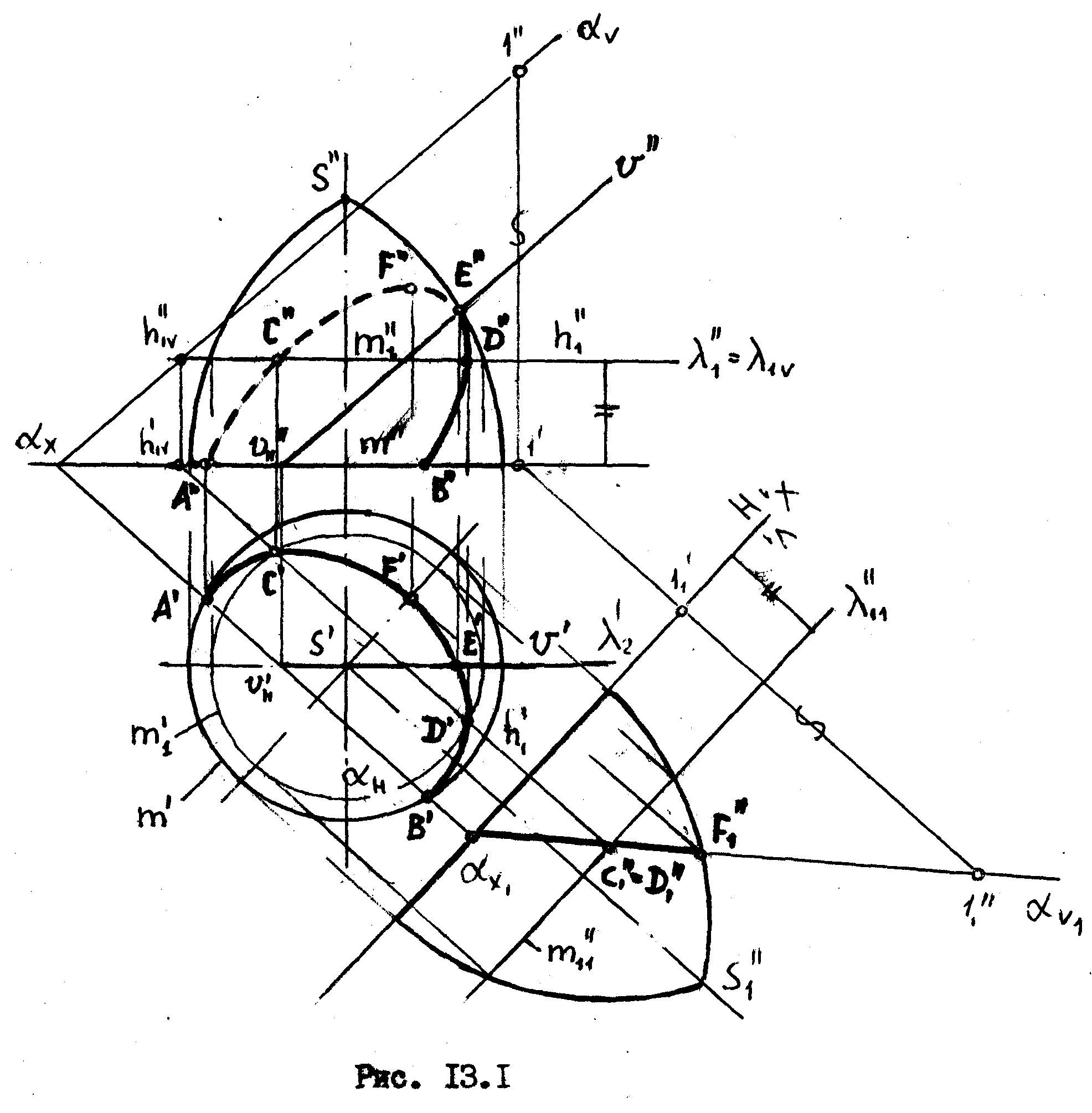
13.3

точки А и В - точки, принадлежащие линии пересечения поверхностей. Прибегая к помощи других горизонтальных секущих плоскостей, будем с их помощью таким же образом получать точки, принадлежащие линии пересечения поверхностей.

Чтобы не загружать чертеж обилеем линий, из этого семейства плоскостей, в качестве примера, возьмем только одну плоскость . Эта плоскость пересечет поверхность по окружности m1, а плоскость - по горизонтали . Пересечение этих линий дает нам искомые точки С и D.

Для определеняя точки Е, в которой кривая сечения на фронтальной проекции из видимой переходит в невидимую / а эта точка всегда лежит на главном меридиане поверхности/, рассечем наши поверхности фронтальной плоскостью . Эта плоскость пе-

13.4

ресечет поверхность по главному меридиану, а плоскость - по фронтали . Пересечение этих линий дает нам точку Е.

Чтобы получить верхнюю точку сечения - точку F, преобразуем чертеж. Введем новую плоскость проекций V1, по отношению к которой плоскость становится проецирующей. На плоскости v1 мы сразу видим верхнюю точку сечения - . Зная эту точку, последовательно находим точки F’и F” .

Примечание

Данную задачу мы могли решить и иным путем. Построив, новую фронтальную плоскость проекций V1 как показано, на рис. 13.1, мы можем в системе плоскостей проекций решить задачу на пересечение поверхности с проецирующей плоскостью . Эта задача более проста, чем задача на пересечение поверхности с плоскостью общего положения. Задачу на построение линии пересечения поверхности с проецирующей плоскостью мы подробно рассмотрели на лекции №11.

Решив эту задачу, т.е. найдя проекции линии пересечения на V1 и H , мы получаем возможность перенести найденные точки, определяющие линию пересечения, на фронтальную плоскость проекций V.

13.4. Взаимное пересечение поверхностей.

Принцип решения подобных задач рассмотрим на примере решения следующей задачи.

Задача.

Построить линию пересечения конуса со сферой /см. рис.

13.2/.

Решение.

При решении данной задачи, как и в предыдущей, целесообразно пользоваться горизонтальными секущими плоскостями, т.к. такие плоскости будут обе заданные поверхности пересекать по простейшим линиям - окружностям. Эти окружности будут без искажения проецироваться на плоскость Н.

Пересечем наши поверхности вспомогательной горизонтальной плоскостью , проходящей через центр сферы. Эта плоскость пересечет сферу по экватору , горизонтальная проекция которого на чертеже уже имеется, а конус эта плоскость пересечет по окружности Пересечение этих окружностей даст нам точки К₁ и K11

13.5

Затем пересечем поверхности плоскостями и ,отстоящими от плоскости на одинаковом расстоянии. Эти плоскости пересекут конус по окружностям m2 и m₃ , а сферу - по окружностям одинакового диаметра n2 и n3 . Пересечение соответствующих окружностей, лежащих в одной и той же плоскости, даст нам, соответственно, точки К₂ ,К₂₁ и К₃ , К31.

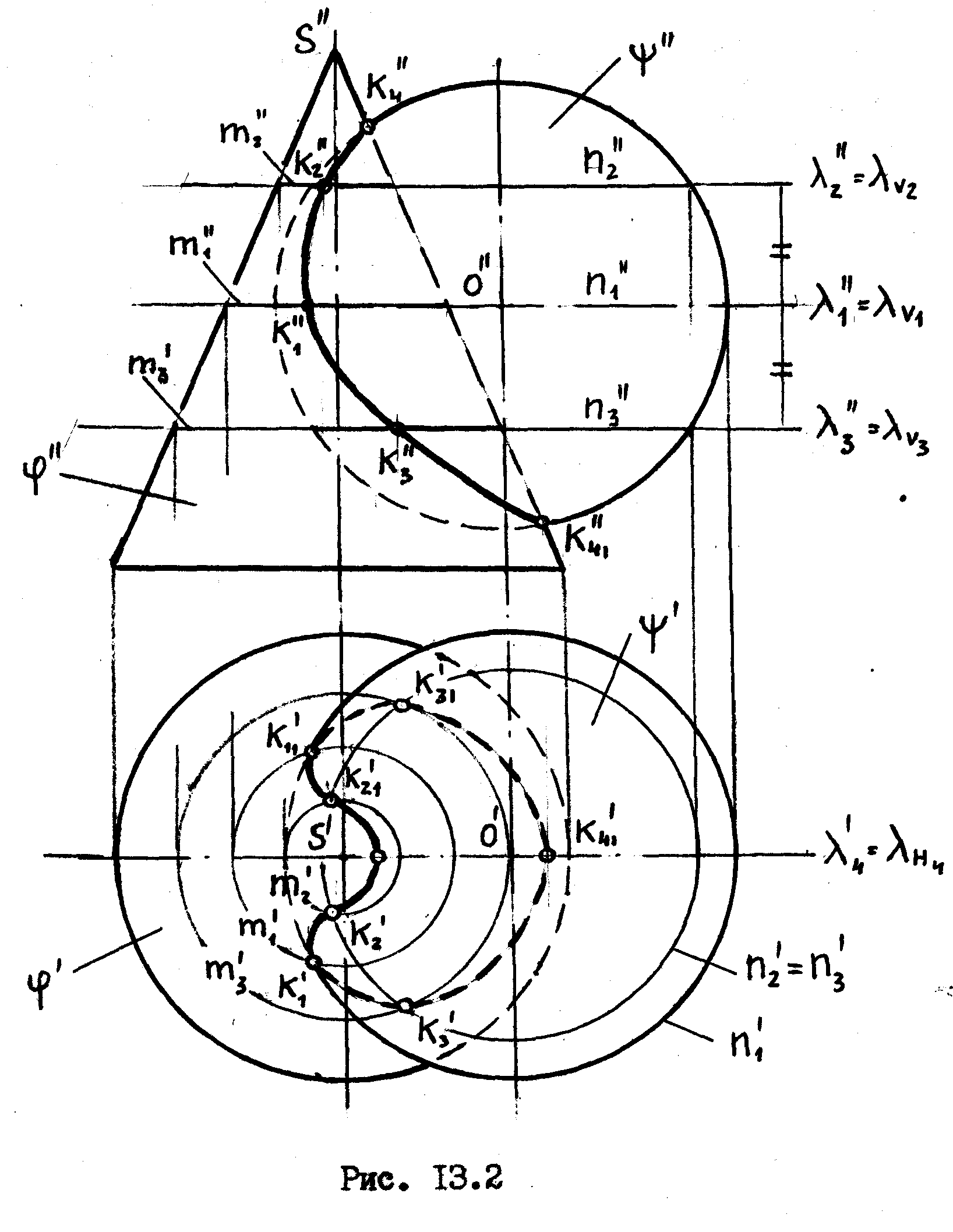
Верхнюю и нижнюю точки линии пересечения мы получим с помощью фронтальной секущей плоскости . Эта плоскость пересечет наши поверхности по их главным меридианам и пересечение этих линий даст нам точки К4 и К41.

13.6

13.5. Особенности пересечення поверхностей второго порядка.

Известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. Поэтому две поверхности второго порядка всегда пересекаются по кривой четвертого порядка. При определённых условиях эта кривая распадается на несколько линий более низкого порядка. При этом сумма порядков линий, на которые распадается кривая, равна порядку самой линии. В частности, кривая четвертого порядка может распадаться на четыре прямых или две кривых второго порядка.

Условия, при которых кривая четвертого порядка распадается на две кривые второго порядка, могут быть сформулированы следующими теоремами.

Теорема I. Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

В учебной литературе эта теорема известна так же, как «теорема Монжа».

Рис. 13.3 дает представление о том, как можно определить линии пересечения конуса и цилиндра , описанных около сферы . Конус соприкасается со сферой по окружности, фронтальная проекция которой есть отрезок [1^”2"], а с цилиндром по окружности, проецирующейся в [3”4”]. Точки пересечения этих окружностей есть точки А и В.

По теореме, плоскости кривых должны проходить через прямую (АВ), а т.к, эта прямая являетея фронтально-проецирущей, то плоскости кривых также будут фронтально-проецирующими. Одна кривая /эллипс/ будет проецироваться отрезком

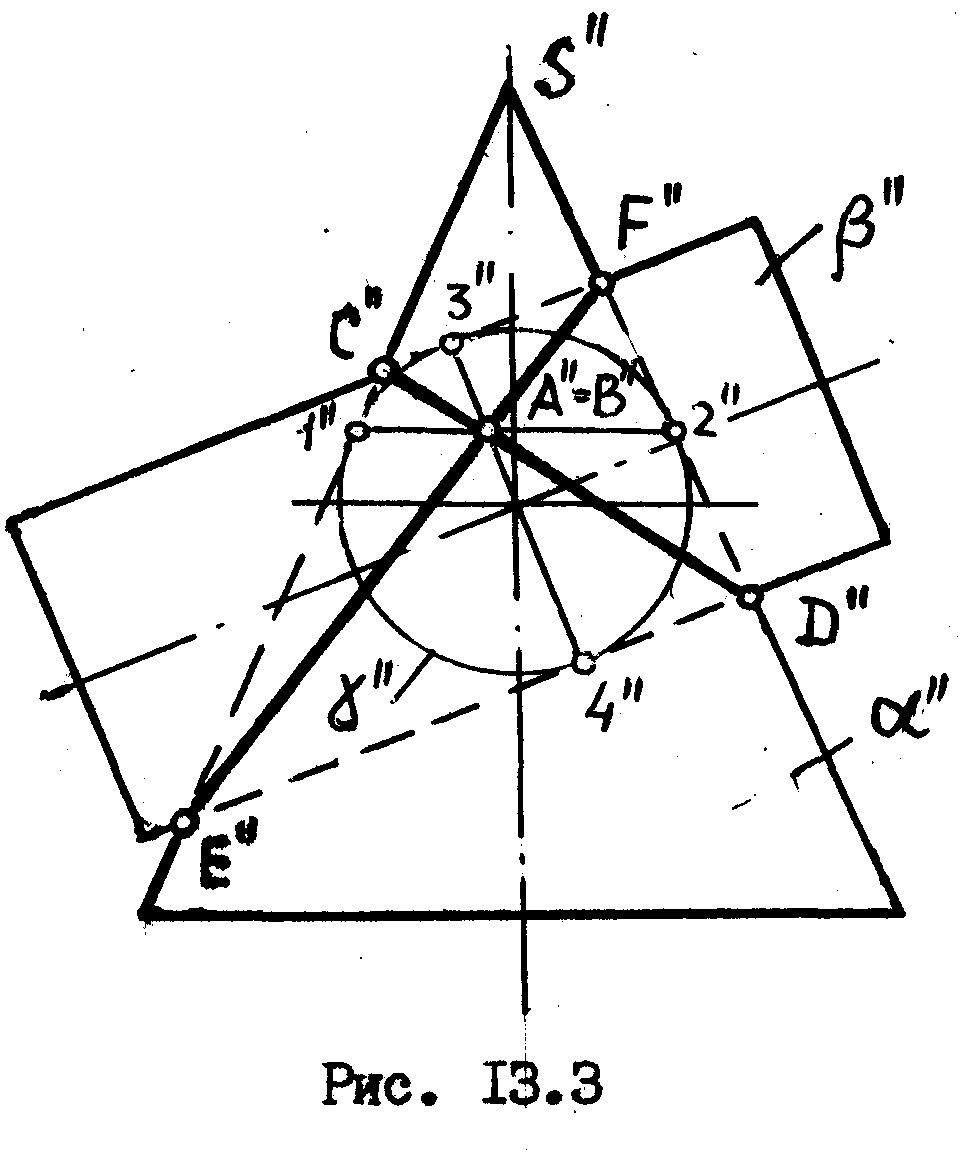
[C”D”] другая /также эллипс/ будет проецироваться отрезвом [Е”F”]

13.7

Теорема 2. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки

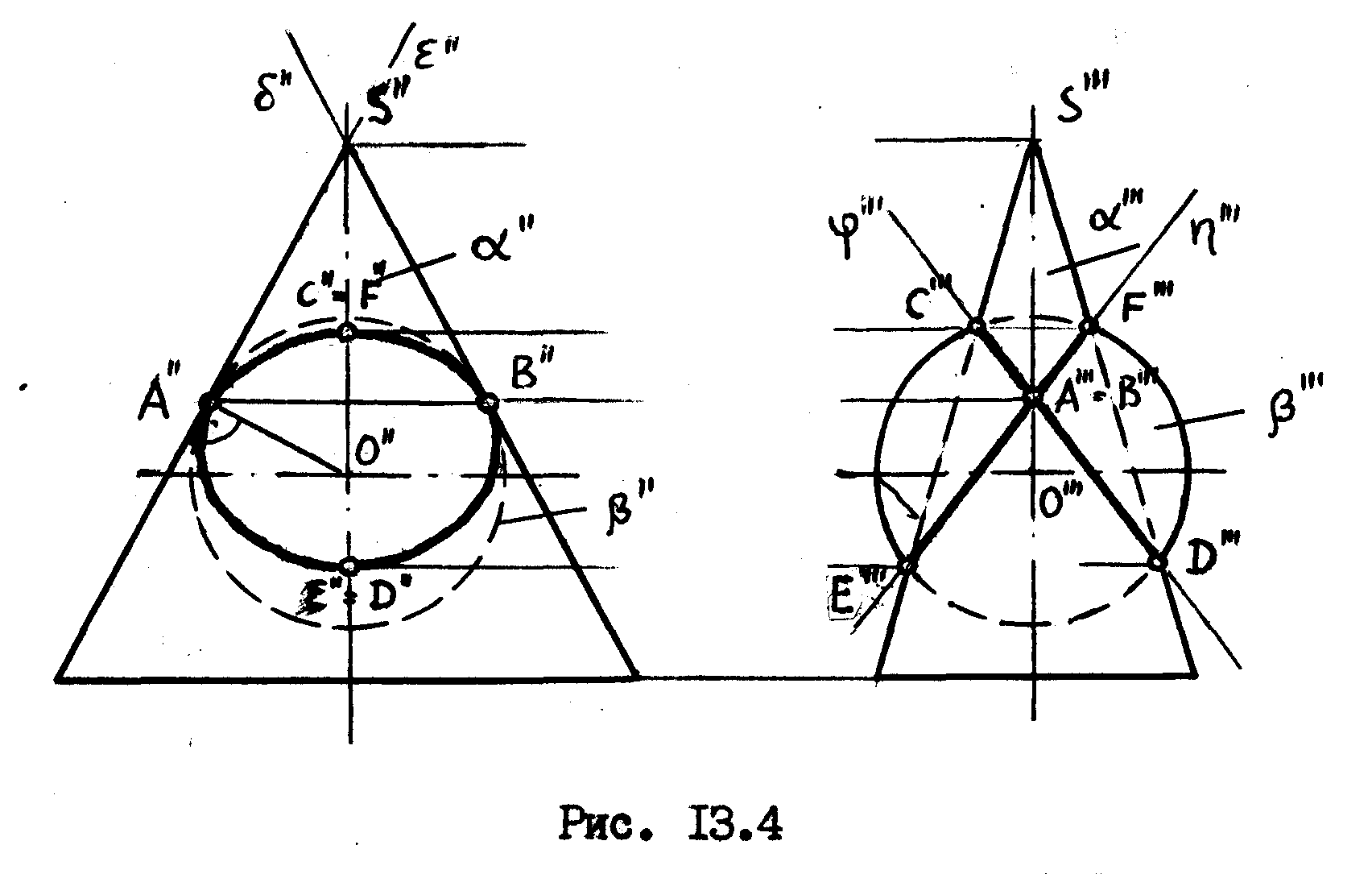
касания.

На рис. 13.4 показано пересечение двух поверхностей второго порядка: эллиптического конуса и сферы . Поверхности и имеют две общие касательные плоскости и и соответственно две общие точки касания А и В . Поэтому по теореме 2 линия пересечения поверхностей распадется на две кривые второго порядка, расположенные в плоскостях и . Эти плоскости проходят через прямую АВ . Так как прямая АВ перпендикулярна плоскости проекций W, то плоскости и будут профильно-проецрущими. Следовательно, принадлежащие им кривые, на плоскость W проецируются в отрезки [C”’D”’] и [E”’F”’]

Следует отметить, что эти кривые будут окружностями, т.к. на сферу нельзя нанести другие плоские кривые.

Последнее обстоятельство позволяет использовать теорему 2 для решения общей задачи на определение положения плоскостей, пересекающих заданные эллиптические поверхности второго порядка по окружностям. Для этого, как и в настоящей задаче, надо в качестве второй поверхности использовать сферу, имеющую с первой поверхностью две точки соприкосновения. Тогда линиями пересечения этих поверхностей будут две окружности, положение которых и определит положение искомых плоскостей. Плоскости, параллельные найденным, будут пересекать заданную

13.8

поверхность также по окружностям, т.к. известно, что параллельные плоскости пересекают поверхности второго порядка по подобным кривым. Так в нашей задаче любая плоскость, параллельная плоскости или плоскости , будет пересекать эллиптический конус по окружности.

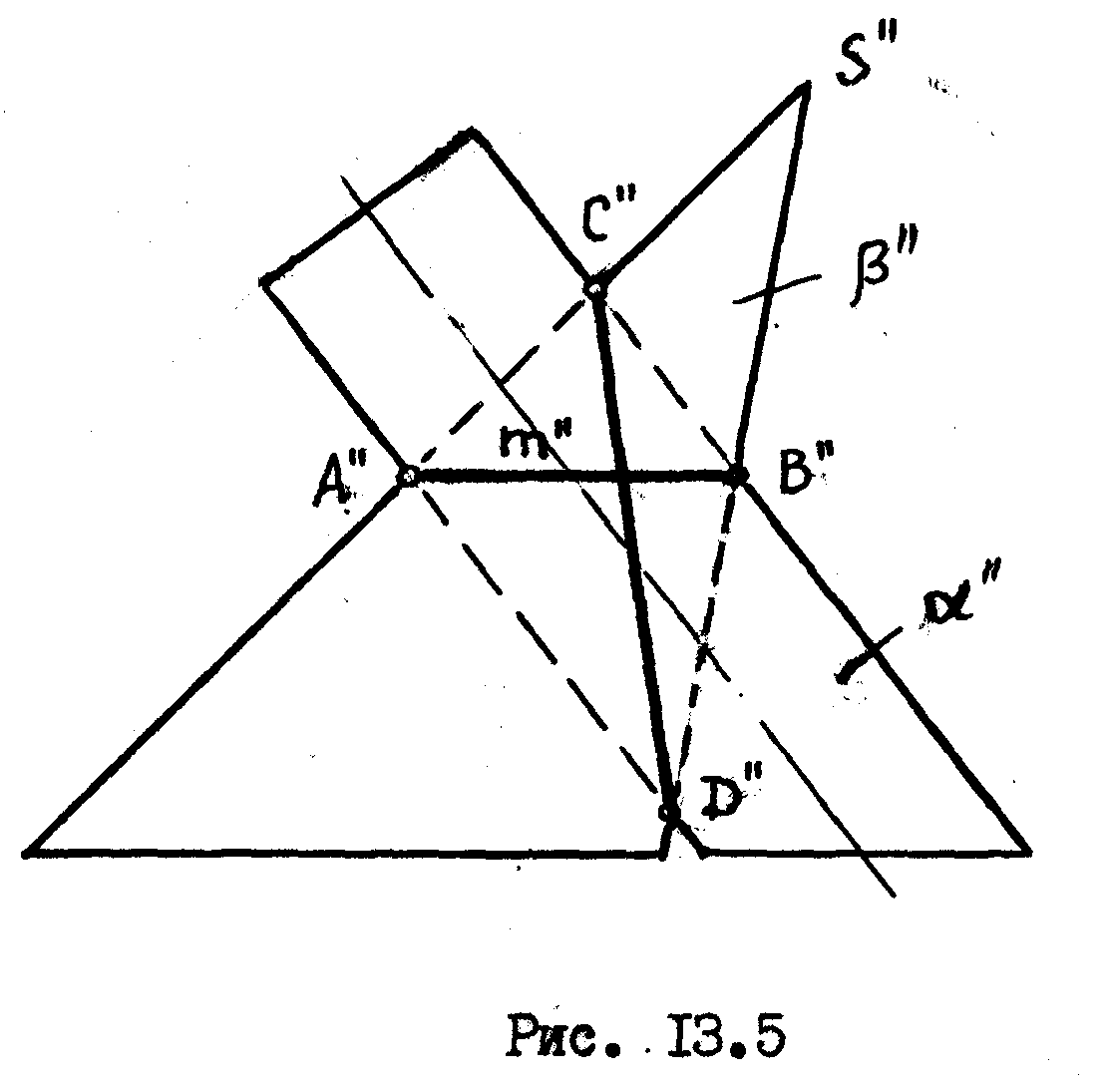Теорема 3. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой.

На рис. 13.5 приведен пример, поясняющий суть теоремы 3. Возьмем окружность m, плоскость которой параллельна плоскости проекций Н. Фронтальная проекция этой окружности, есть отрезок A”B”. Взяв эту окружность в качестве направляющей, опишем наклонный цилиндр и конус с произвольной вершиной S. И цилиндр, и конус будут эллиптическими.

Очевидно, что окружность m будет одной из кривой пересечения наших поверхностей. В соответствии с теоремой 3 наши поверхности должны пересечься еще по одной плоской кривой. Такой кривой будет эллипс, фронтальная проекция которого будет C”D”.

Примечание.

Если изложение п.п. 13.3 и 13.4 отнимет много времени, то материал п. 13.5 может быть изложен частично. В этом случае следует лишь пояснить теорему I /теорему Монжа/, а теоремы 2

13.9

и 3 можно опустить.

Материал лекции №13 изложен в учебнике С.А.Фролова /изд. 1978 г./ на стр. 116-118, 124-127, 131-132, 145-147.

14.1

Л Е К Ц И Я №14

Тема лекции.

Взаимное пересечение поверхностей. Построение линии пересечения поверхностей методом вспомогательных секущих сфер. Построение разверток.

Содержание лекции.

Пересечение двух соосных поверхностей вращения. Построение линии пересечения двух поверхностей вращения, оси которых пересекаются. Область применения метода вспомогательных секущих сфер. Построение разверток поверхностей цилиндра и конуса.

14.1.Построение двух соосных поверхностей вращения.

Соосными называются поверхности, имеющие общую ось вращения. Две соосные поверхности вращения пересекаются между собой по окружности, плоскость которой перпендикулярна оси поверхности. Если общая ось поверхностей параллельна плоскости проекций, то на эту плоскость проекций окружность будет проецироваться прямой линией /рис. 14.1а/. Если одной из этих поверхностей будет сфера и её центр будет принадлежать оси другой поверхности, то сфера пересечется с этой поверхностью тоже по окружностям, проекции которых, при наличии вышеупомянутых условий, будут представлять собой, как и в первом сдучае, прямые линии.

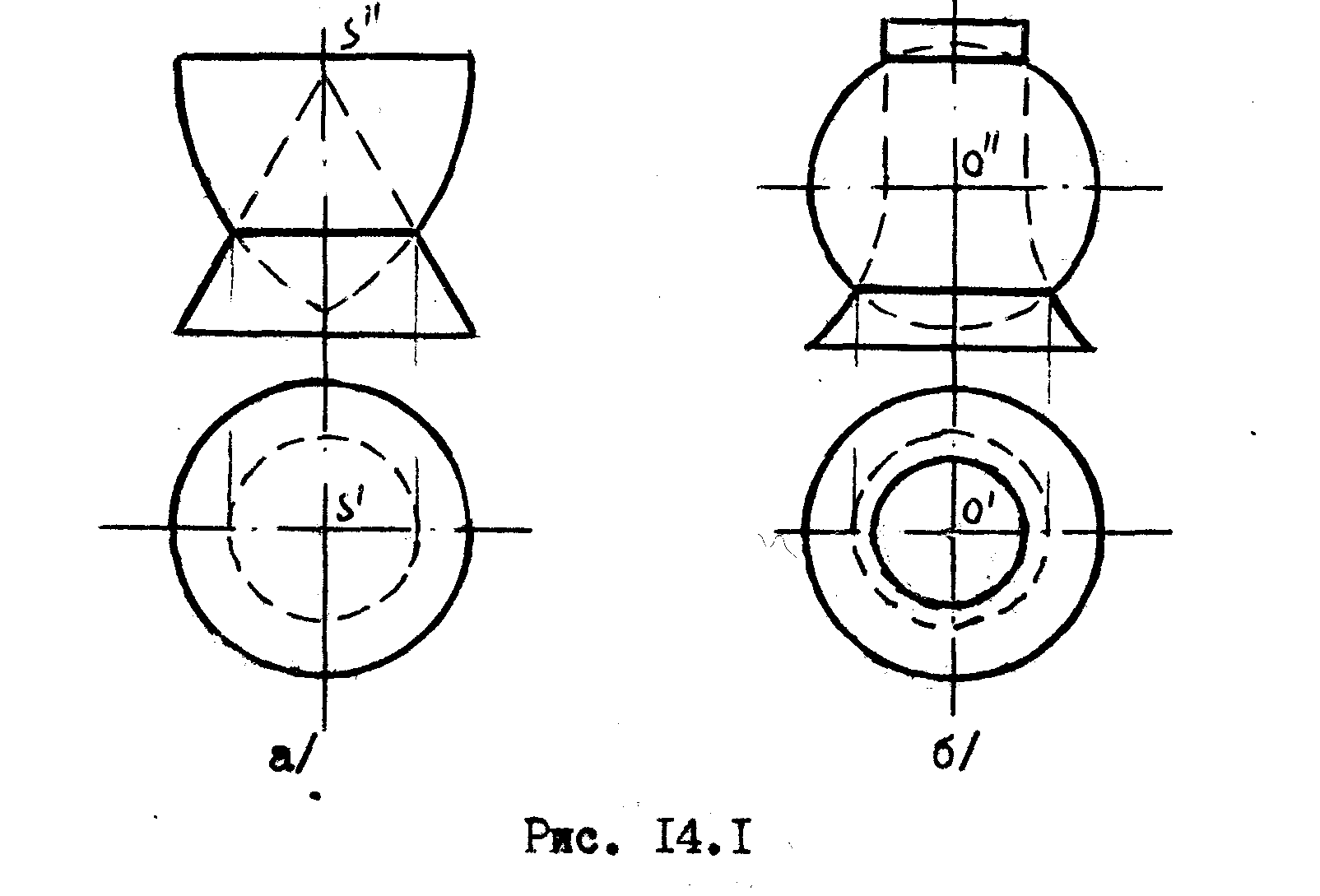
14.2

Используя это свойство, можно в некоторых задачах на построение линии пересечения поверхностей вместо вспомогательных секущих плоскостей использовать в с п о м о г а т е л ь н ы е

с е к у щ и е с ф е р ы.

14.2. Построение линии пересечения двух поверхностей вращения.

Рассмотрим применение метода вспомогательных секущих сфер на следующих задачах.

Задача I.

Построить линию пересечения двух поверхностей вращения

/рис. 14.2/.

Для того чтобы секущая сфера пересекла каждую поверхность по окружности необходимо, чтобы центр сферы лежал на оси каждой поверхности. Это условие будет выполнено в том случае, если центр сферы будет совпадать с точкой пересечения осей.

Сферой минимального радиуса окажется сфера, касательная к поверхности вращения, имеющей вертикальную ось. Эта сфера коснется поверхности по окружности /1,2/, а вторую поверхность - конус, пересечет по окружности /3,4/. Если провести сферу меньшего диаметра, то она, пересекаясь с конусом, уже не будет пересекаться с поверхностью вращения и, следовательно, с ее помощью мы не получим решения.

Пресечение окружностей /1,2/ и /3,4/ даст нам точку С, принадлежащей искомой линии пересечения наших поверхностей.

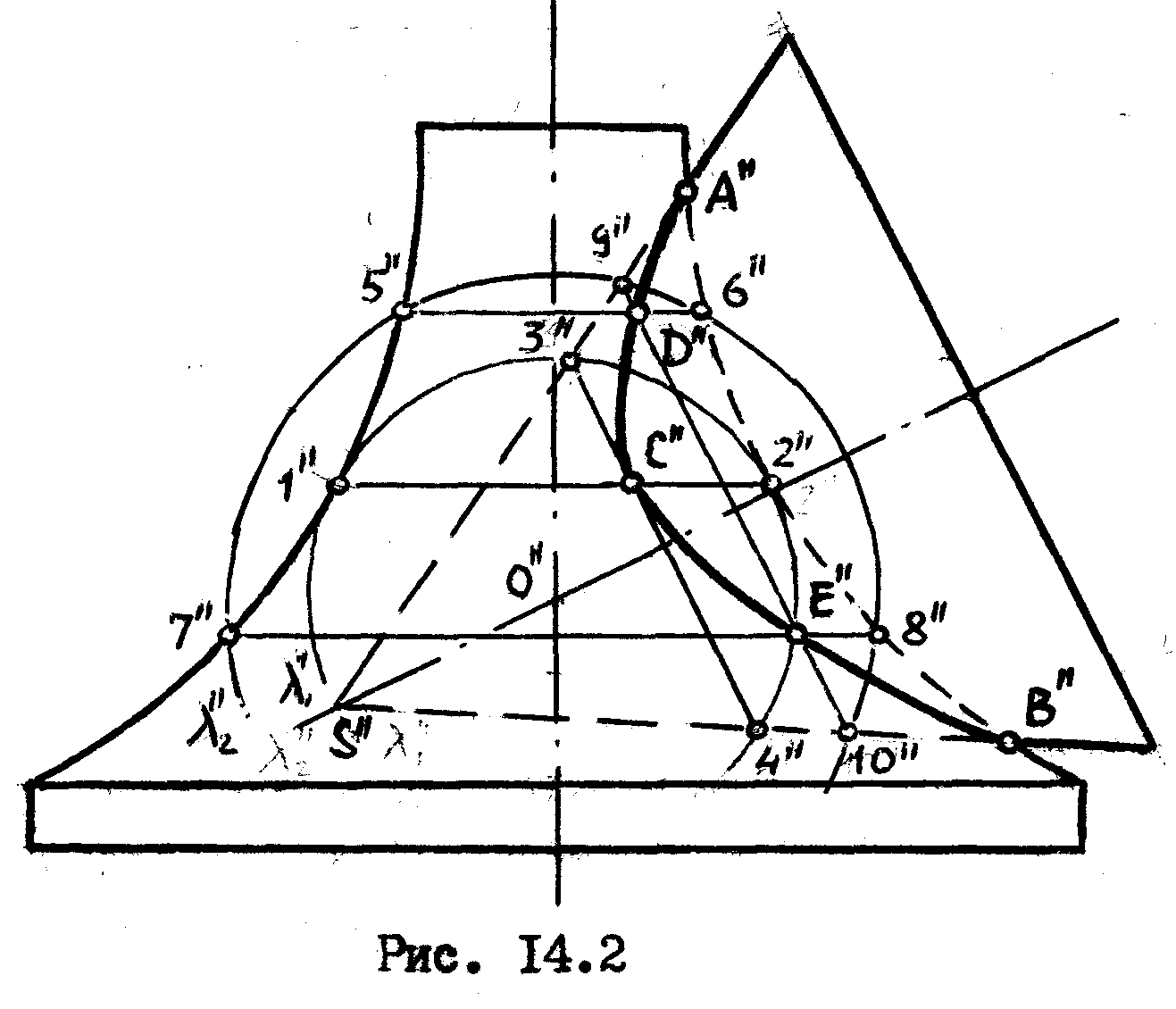
14.3

Построив вторую сферу , мы, с ее помощью, получим уже две интересущие нас точки - D и Е.

Следует отметить, что данная задача, очень просто решаемая методом секущих сфер, трудно выполнима при ее решении методом секущих плоскостей. Трудность решения последним способом состоит в том, что в данной задаче не существует такого положения секущих плоскостей, при котором обе поверхности одновременно пересекались бы по простейшим кривым. Так, например, семейство горизонтальных секущих плоскостей, рассекая поверхность вращения по простейшим линиям - окружностям, будут пересекать конус по сложным кривым - гиперболам. Последнее обстоятельство создаст большие затруднения при решении задачи.

Задача 2. Построить линию пересечения кругового конуса со сферой.

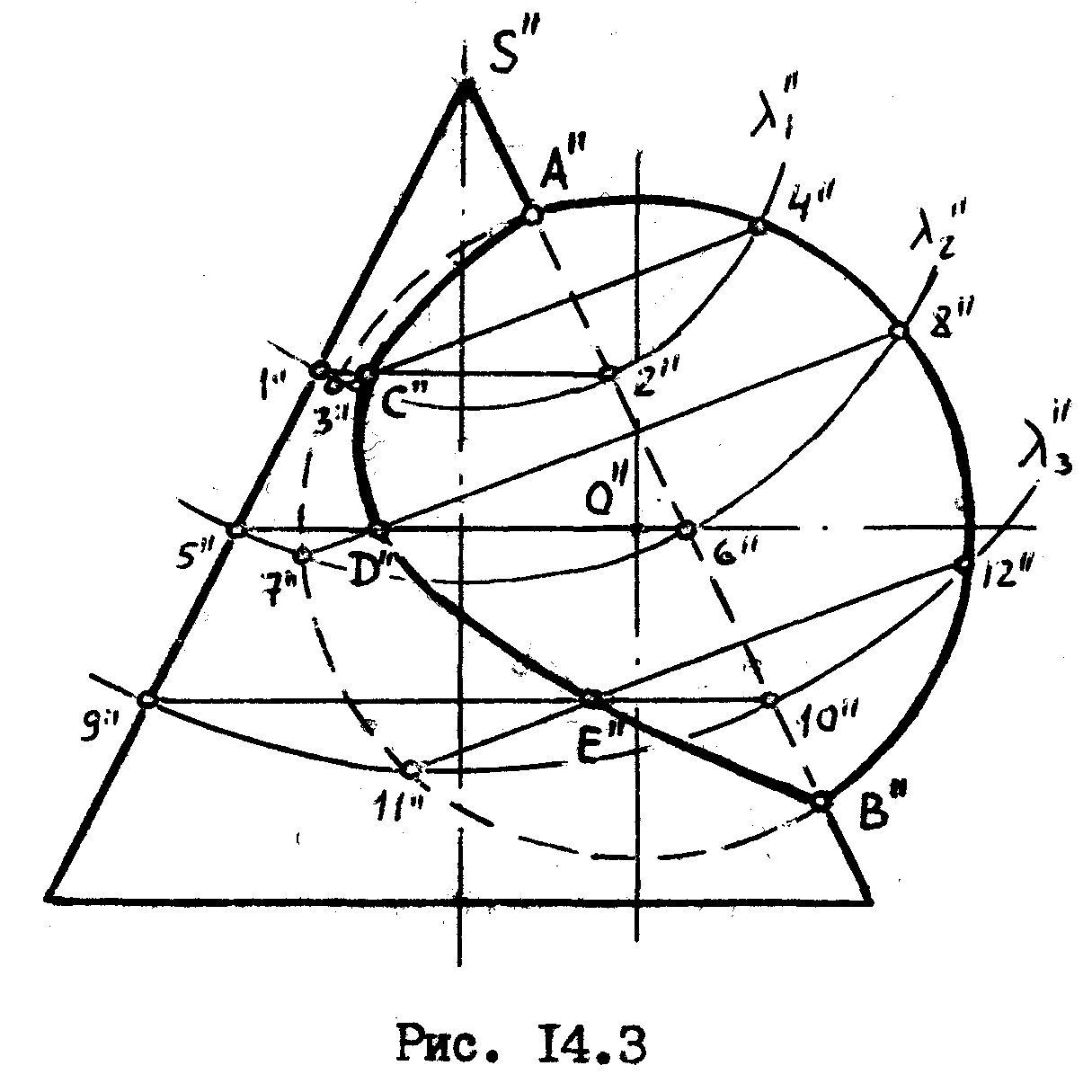
Эта задача была решена на прошлой лекции методом вспомогательных секущих плоскостей. Для сравнения рассмотрим ее решение методом вспомогательных секущих сфер. Эта задача имеет одну особенность, которой не было в предыдущей задаче. Дело в том, что сфера имеет бесчисленное множество осей, вследствие чего за центр секущих сфер можно принять любую точку, принадлежащую оси конуса, т.к. через эту произвольную точку всегда можно провести новую ось сферы. В качестве такой произвольной

14.4

точки может быть выбрана и вершина конуса S.

Решение задачи ясно из чертежа. Это решение следует подробно пояснить слушателям.

После решения приведенных задач следует обратить внимание студентов, что при их решении мы использовали только о д н у плоскость проекций и именно ту, по отношению к которой оси поверхностей параллельны. Это обстоятельство является одной из особенностей метода вспомогательных секущих сфер.

При применении метода вспомогательных секущих плоскостей решение задач с использованием только одного поля проекций совершенно невозможно.

Если у нас возникнет необходимость построить вторую проекцию линии пересечения, это можно будет легко сделать обычным путем, т.е. исходя из условия принадлежности линии пересечения одной из данных нам поверхностей.

14.3. Область применения метода вспомогательных секущих сфер.

Метод вспомогательных секущих сфер, дающий в некоторых случаях значительно более простые решения_, чем метод вспомогательных секущих плоскостей, к сожалению, не столь универсален как последний метод и может быть применен в ограниченных случаях, при наличии определенных условий.

Метод вспомогательных секущих сфер применим только в тех случаях, когда

о д н о в р е м е н н о выполняются следующие три условия.

1. Обе поверхности должны быть поверхностями вращения, или одна -

поверхностью вращения, другая - не являясь поверхностью

вращения, должна содержать круговые сечения.

2. Оси поверхностей должны пересекаться.

3. Оси обеих поверхностей должны быть параллельны плоскости

чертежа.

В рассмотренных выше задачах эти три условия были в наличии.

14.4 Построение разверток поверхностей.

Развертывающимися поверхностями называются поверхности, которые путем изгибания, без разрывов и образования складок, могут быть совмещены с плоскостью. Естественно, что к группе развертывающихся поверхностей могут быть отнесены только линейчатые поверхности и, в частности, те из них, которые имеют пе-

14.5

ресекающиеся смежные образующие. Точка пересечения образующих может быть как собственной /коническая поверхность/, так и несобственной /цилиндрическая поверхнооть/.

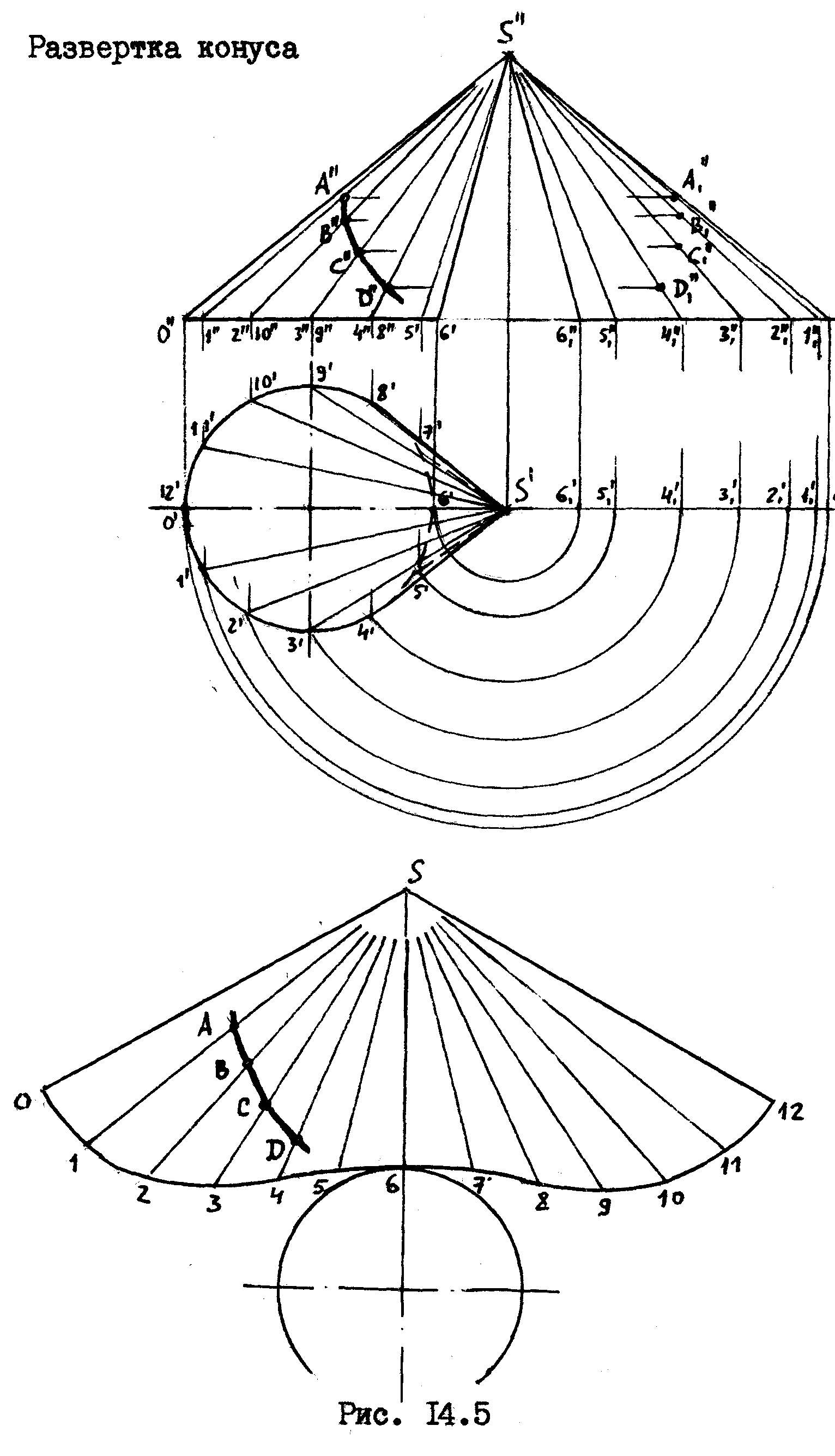
Неразвертываемые поверхности, /например, сфера/ могут быть развернуты только приближенно. Задачи приближенного развертывания поверхностей мы рассматривать не будем. Рассмотрим построение разверток развертываемых поверхностей - цилиндра и конуса.

Развертка цилиндра.

При построении развертки данного прямого кругового цилиндра /рис.14.4/ окружность основания цилиндра следует разделить на равные части / в нашем примере их 12/. Длину хорды, соединяющей соседние точки, можно приближенно принять за длину дуги между теми же точками, к примеру, и.т.д. Преследуя большую точность построения,можно аналитически подсчитать длину окружности основания цилиндра и отложить ее на развертке, а затем полученный отрезок разделить на прежнее количество частей /0,1,2,..12/.

Длины соответсвующих образующих берутся с фронтальной про

14.6

екции цилиндра, где они проецируются в натуральную величину.

Если на поверхности цилиндра задана линия 1 /своей фронтальной проекцией-1"/, то перенося на соотестствующие образующие точки А,В,С,...., принадлежащие этой линии, получаем положение линии 1 на развертке.

14.7

При развертке наклонного конуса обычно применяется следующий прием. Боковая поверхность конуса заменяется вписанной в нее многогранной пирамидальной поверхностью. Чем больше будет число граней у вписанной пирамиды, тем меньше будет разница между действительной и приближенной разверткой конуса. В нашем примере /рис.14.5/ окружность основания конуса разбита на 12 равных частей. Следовательно, поверхность конуса заменяется поверхностью двенадцатигранной пирамиды. Перед построением развертки целесообразно заранее определить истинную длину всех намеченных образующих. На чертеже /рис.14.5а/ это сделано способом вращения образующих вокрут вертикальной оси, проходящей через вершину конуса

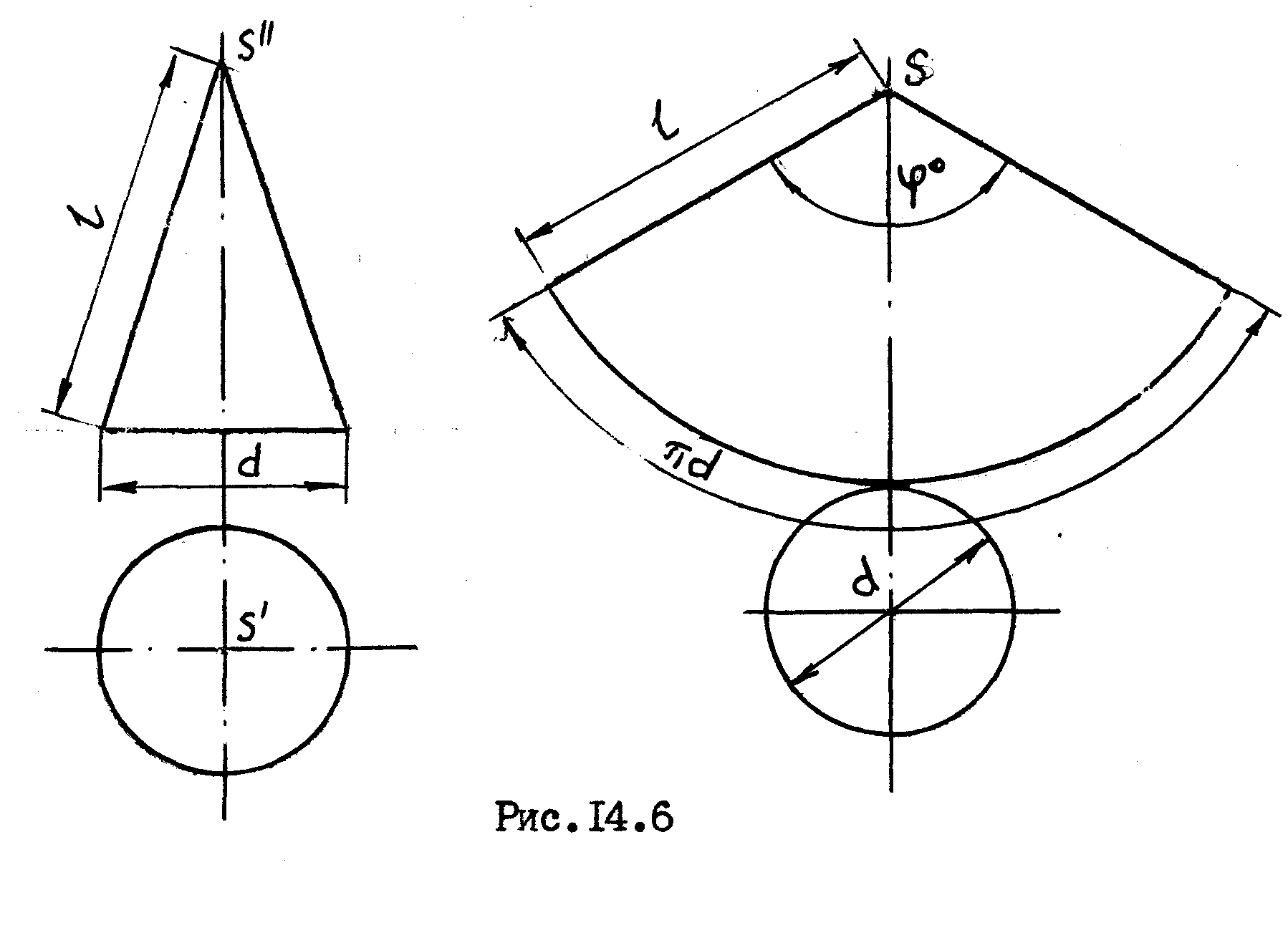
S. Строя последовательно один за другим натуральную величину треугольников /граней пирамиды/ и соединяя плавной линией точки 0,1,2,3,..., получаем развертку боковой поверхности конуса /рис.14.5б/.

Если на конусе нанесена линия l /задана своей фронтальной проекцией l” /, то перенося точки А,В,С,... этой кривой на натуральные величины соответствующих образующих, а затем откладывая их расстояния от вершны S, получаем линию 1 на развертке /рис.14.5б/. К примеру- .

Развертка прямого кругового конуса строится значительно проще. Его развертка представляет собой сектор окружности радиуса 1 /где 1-- длина образующей конуса/.

Такой конус и его развертка приведены на рис. 14.6.

14.8