7.4 Взаимная перпендикулярность прямых.
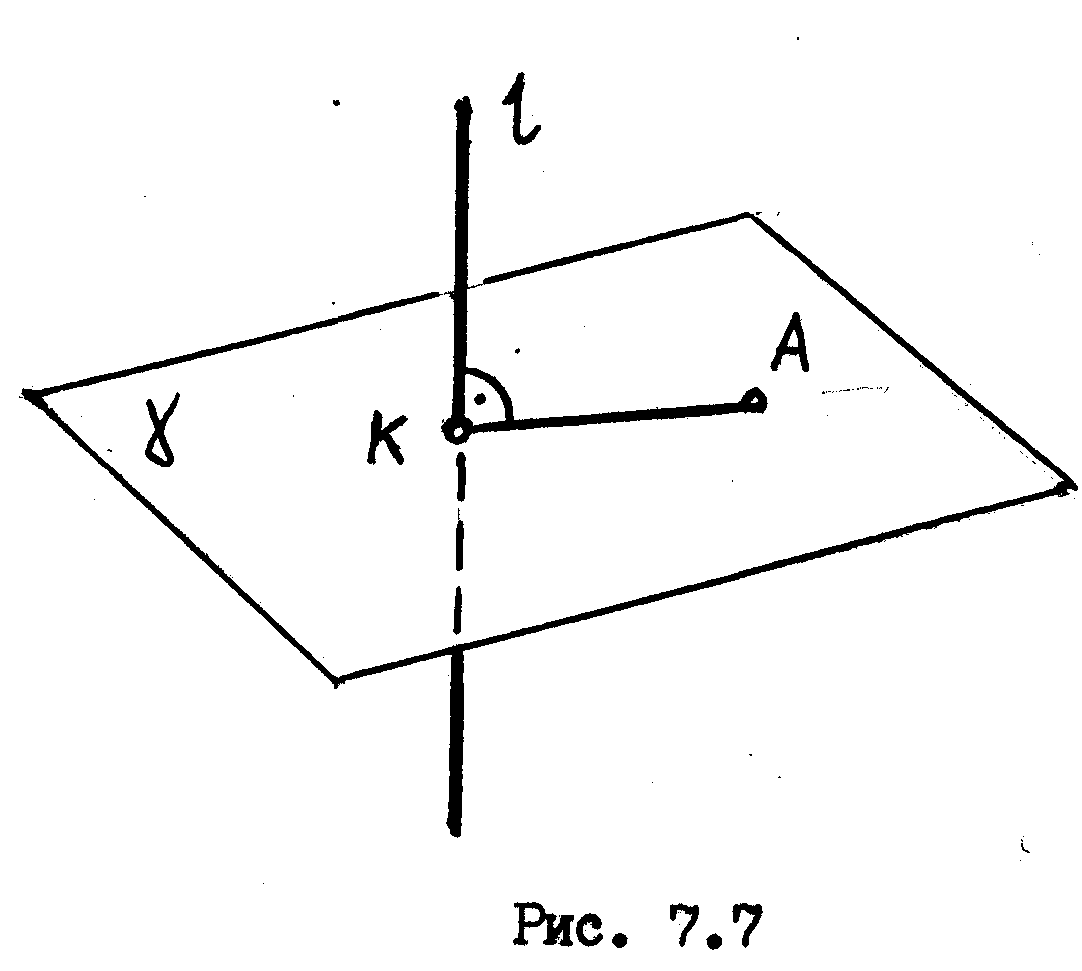
Учитывая, что прямой угол, образуемый двумя прямыми, в общем случае будет проецироваться с искажением, задача на построение перпендикуляра к прямой может быть выполнена при условии следования следующему алгоритму решения./рис. 7.7/.
7.6
Для того, чтобы из точки А опустить перпендикуляр на прямую l необходимо проделать следующие операции.
I.
Через точку А
провести
плоскость
,
перпендикулярную l.
2.
Найти точку К
- точку пересечения прямой l
с плоскостью
.
3. ,Провести отрезок АК, который и будет перпендикуляром, опущенным из точки А на прямую 1.
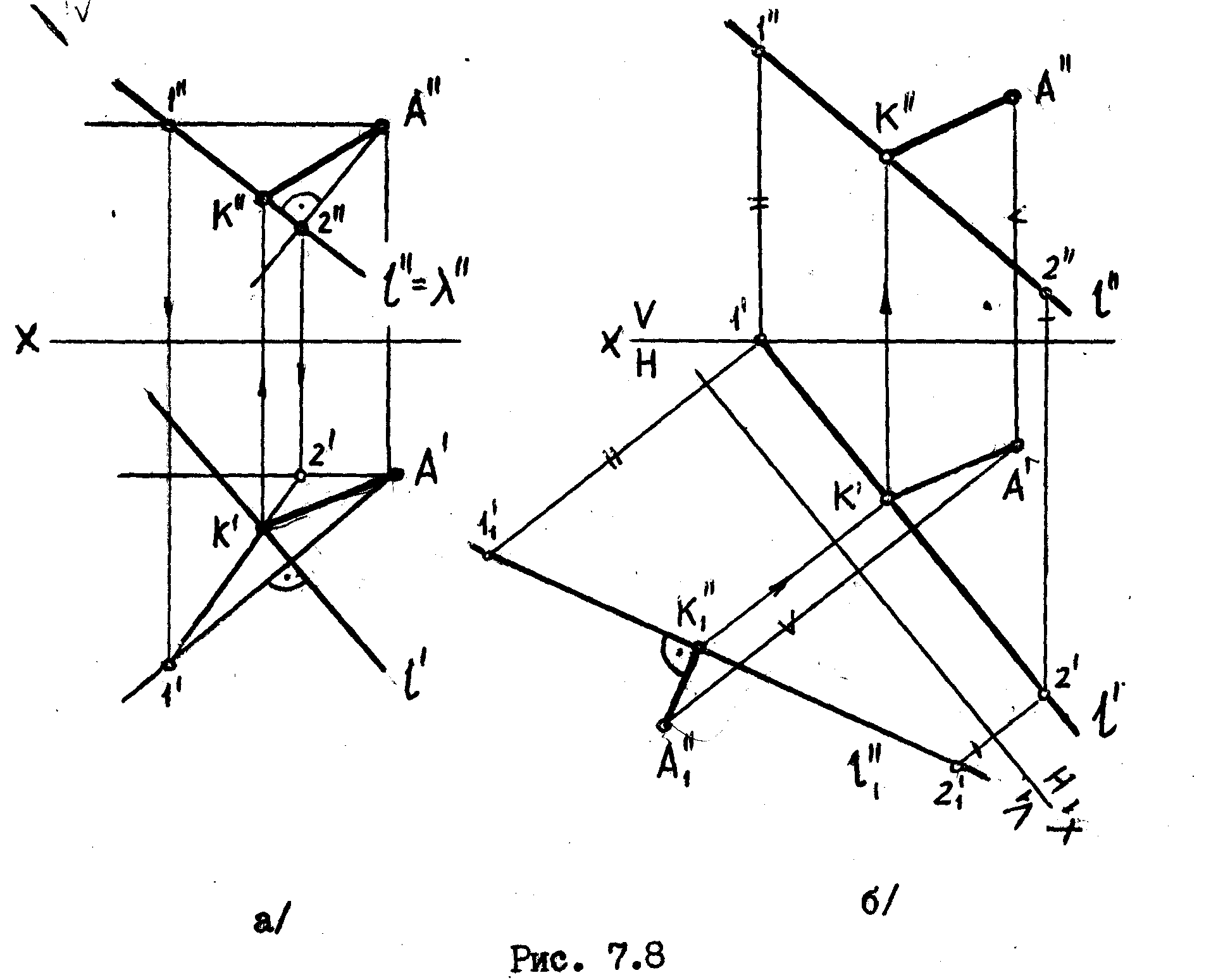
Используя этот алгоритм, решим задачу на комплексном чертеже /рис. 7.8а/
Решение
1.
Через точку А
проводим плоскость
,
перпендикулярную прямой l
, задавая ее горизонталью h
и фронталью
.
Строим
эти
прямые так, что
2.
Ищем точку пересечения прямой 1
с плоскостью
.
Для этого заключаем прямую l
во фронтально-проецирующую плоскость
.
Эта плоскость пересечет плоскость
по линии 1-2, которая и даст нам искомую
точку К.
3. Отрезок АК и будет перпендикуляром, опущенным из точки А на прямую l.
Как видим из чертежа, прямой угол между прямой и отрезком АК ни на одну плоскость проекций не проецируется прямым углом, т.к. ни та, ни другая прямая не параллельна ни одной из плоскостей проекций.
7.7
Эта
задача может быть решена и иным путем.
Помня о том, что прямой угол проецируется
прямым углом тогда, когда одна из его
сторон параллельна плоскости проекций,
мы преобразуем чертеж. /см рис. 7.8 б /.
Вводим новую плоскость проекций-V1,
параллельную
прямой l
.
Тогда на эту плоскость проекций прямой
угол спроецируется прямым углом. Строим
отрезок
.
Найдя
точку
,
строим затем горизонтальные и фронтальные
проекции
точки К
и искомого отрезка АК.
Примечание
Следует
обратить внимание студентов на очень
распространенную ошибку, часто ими
допускаемую. Многие из них ошибочно
считают, что отрезок
является
его
натуральной
величиной.
Следует
пояснить , что на V1
проецируется в натуральную величину
только угол , а сторона этого угла АК
в системе плоскостей
являемся прямой общего положения, и по
этой причине не может проецироваться
в натуральную величину
7.8
7.5 Взаимная перпендикулярность плоскостей.
Пучек
плоскостей
....
/рис. 7.9/ перпендикулярен плоскости
,
т.к. ось пучка - прямая n
перпендикулярна плоскости
Итак,
запомним правило. Плоскость
будет перпендикулярна к плоскости
в том случае, если плоскость
будет содержать в себе прямую,
перпендикулярную к плоскости
.
Задача
Через
прямую m
провести
плоскость
,
перпендикулярную к плоскости
,/рис.
7.10/
Через
точку
,
проводем прямую, перпендикулярную
плоскости
.
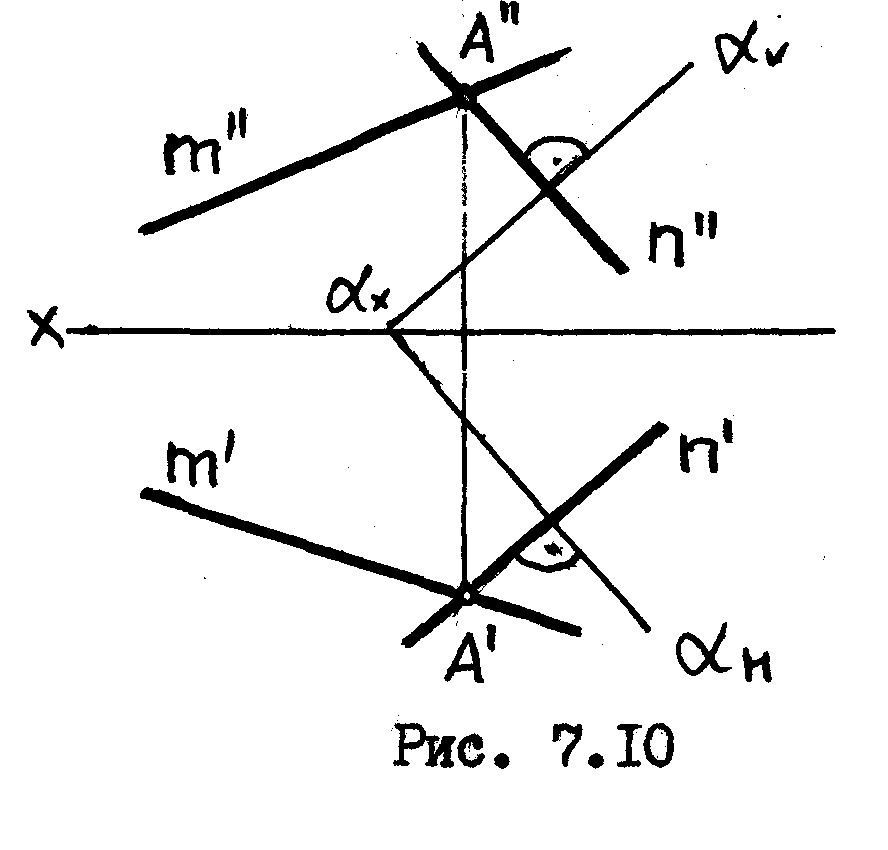Прямые
m
и n,
как две пересекающиеся прямые, определяют
собой плоскость
,
перпендикулярную к плоекости
.
. Задача
Дано: треугольник АВС, сторона DE и фронтальная проекция треугольника DEF. Построить горизонтальную проекцию треугольника
DEF, если известно, что плоскости треугольников, взаимно- перпендикулярны /рис. 7.11/.
Решение:
Для
того, чтобы треугольник DEF
был перпендикулярен к плоскости
треугольника АВС,
он должен содержать в себе прямую,
перпендикулярную к плоскости треугольника
АВС.
Строим такую прямую n
проходящую
через вершну F.
Для этого, предварительно, в треугольнике
АВС
строим горизонталь
h
и
фронталь
,
7.9
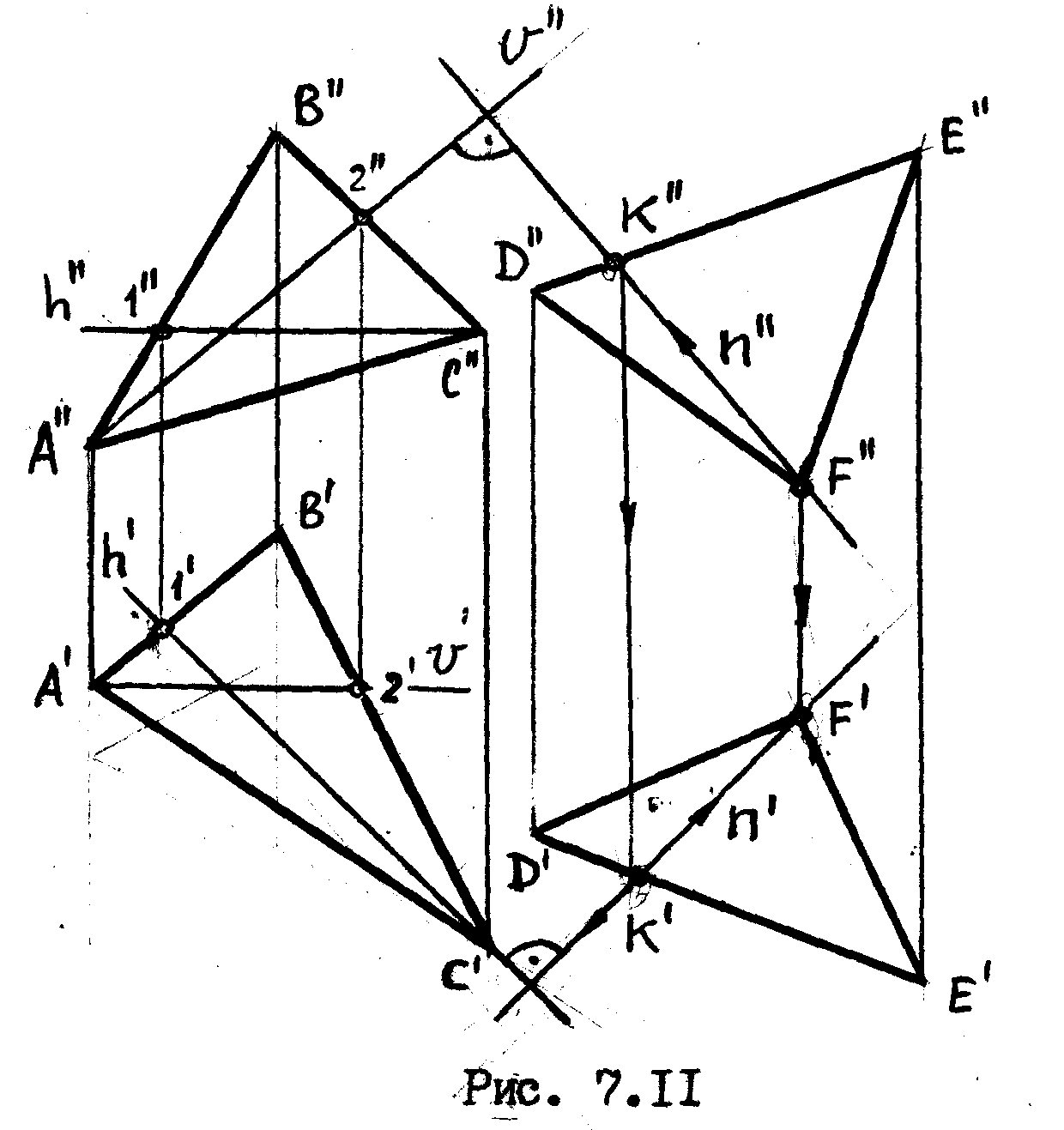
после
чего строим прямую n.
При этом
.
Прямая n
пересекает
сторону DЕ
в точке К.
Определив положение n'
находим
F’и,
следовательно, определяем горизонтальную
проекцию треугольника DEF.
Содержание лекции №7 изложено в учебнике С.А.Фролова /изд.1978г./ на стр. 159-161, 164-168.
8.1
-
Л Е К Ц И Я №8
Тема лекции
Определение расстояний.
Содержание лекции.
Определение расстояний от точки до прямой, между прямыми, от точки до плоскости, между плоскостями.
8. Определение расстояний
При решегош практических задач мы должны рассмотреть сле-дущие задачи на определенив истинных значений расетояний.
1-ая группа задач.
1. От точки А до точки В .
2-ая группа задач.
2. От точки А до прямой m.
3. От прямой а до параллельной ей прямой m.
4. От прямой а до скрещиващейся с ней прямой m .
3- яя группа задач.
5.
От точки А
до
гагоскоети
.
6.
От прямой a
до параллельной ей плоскости
.
7.
От плоскости
до параллельной ей плоскости
.
Практически, все задачи от 2-ой до 7-ой сводятся к задаче первой, т.к. во всех перечисленных случаях ставится задача на отыскание длины отрезка, определяющего все перечисленные расстояния. Вся сложность этих задач состоит лишь в том, что надо суметь правильно построить этот отрезок.
Задачи на определение расстояний разбиты на 3 группы. Каждая из этих групп имеет свой алгоритм решения.
8.1.Первая группа задач.
Эта группа состоит всего из одной задачи - определении расстояния между двумя точками, т.е. определении натуральной величины отрезка, соединяющего эти точки.
Эту задачу мы сейчас не будем рассматривать, т.к. мы ее изучали во всех подробностях на предыдущих лекциях.
8.2
Так, в частности, с определением натуральной величиин отрезка способом прямоугольного треугольника мы познакомились на лекции № 2. Определение натуральиой величины отрезка мы производили также различными методами преобразования чертежа, решая первую задачу на преобразование, суть которой состояла в преобразовании отрезка прямой общего положения в отрезок прамой уровня, когда этот отрезок проецировался в натуральную величину./ см. лекции №5 и №6/.
8.2. Вторая группа задач.
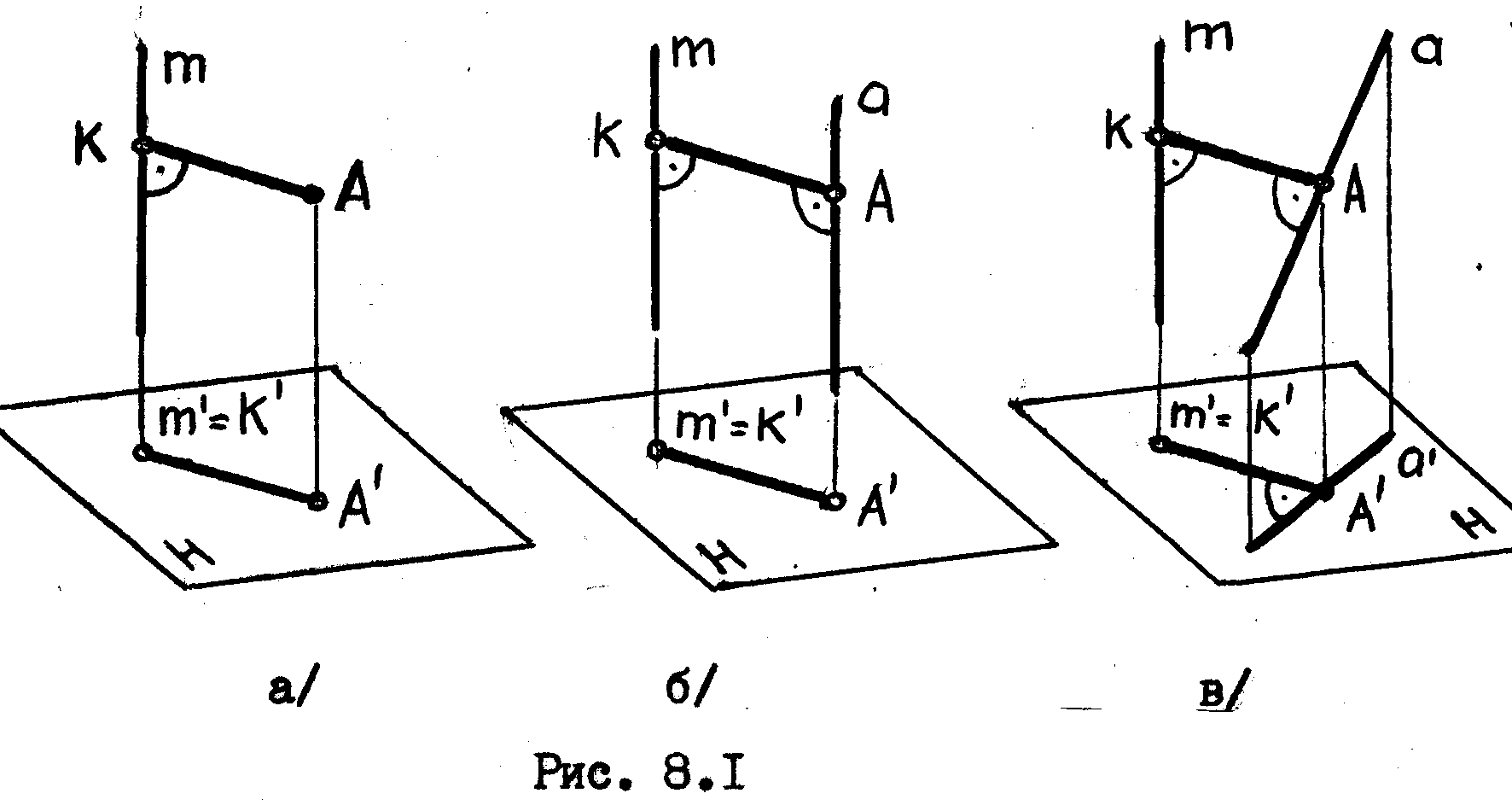
Из рис. 8.1 мы видим, что расстояния, определяемые в задачах второй группы /задачи №№ 2,3,4/, будут проецироваться на плоскость проекций в натуральную величину в том случае, если прямая m будет проецирующей по отношению к этой плоскости проекций.
Следовательно, для решения этой группы задач следует применить вторую основную задачу на преобразование чертежа.
Напомним, что второй задачей на преобразование мы называем преобразование прямой общего положения в проецирующую.
Рассмотрим решение двух задач из этой группы.
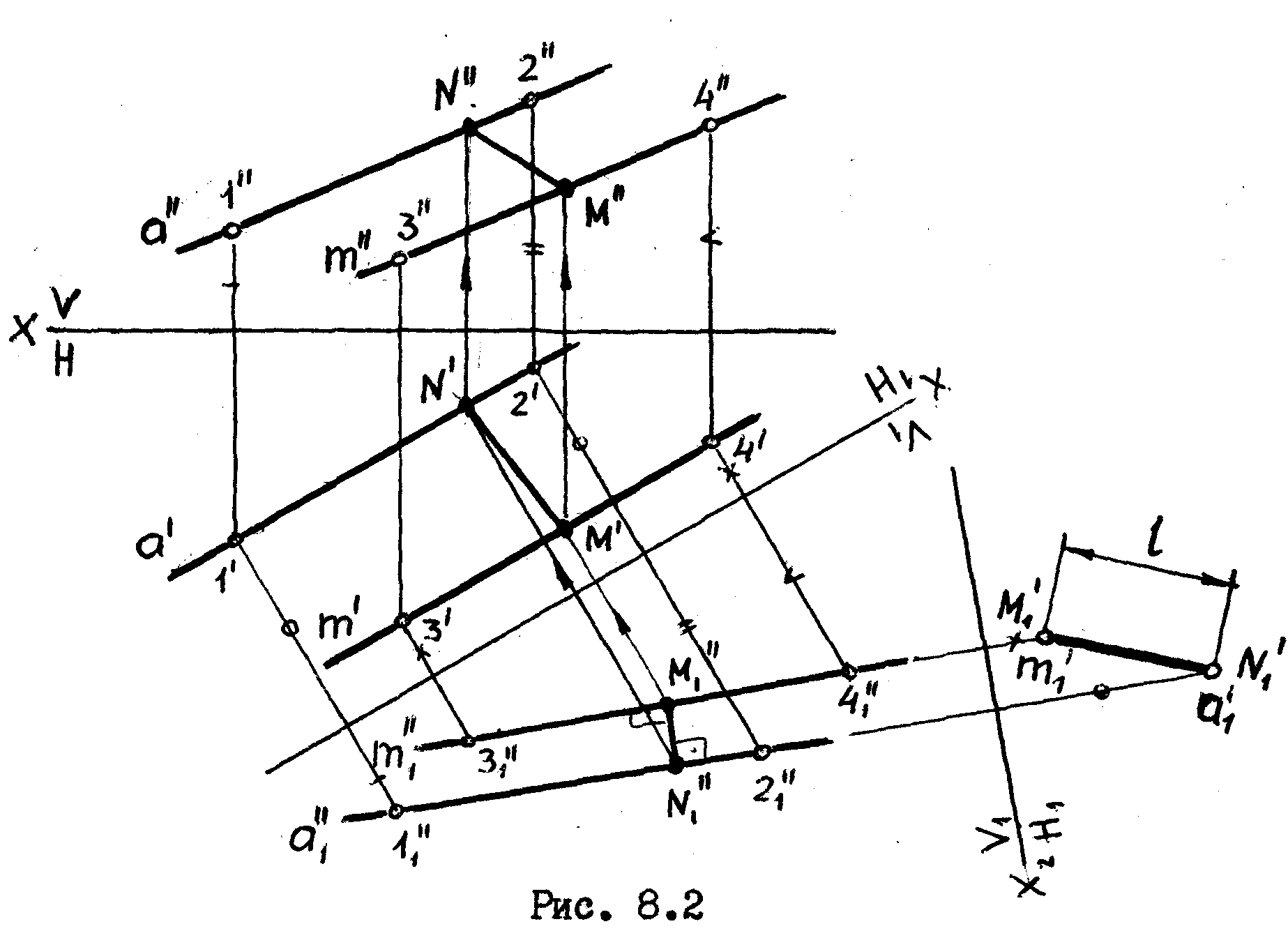
Задача
Определить расстояние между параллельными прямыми a и m,
/ рис. 8.2/
Решение
Путем замены плоскостей проекций превращаем прямые в проецирующие. На плоскости Н1 мы видим истинную величину расстояния между этими прямыми.
8.3
Указание
Построив
на Н1
проекцию отрезка
,
определяющего собой расстояние между
прямыми, полезно "вернуться назад",
т.е. показать проекции этого отрезка на
исходных плоскостях проекций. Отрезок
может быть взят в любом удобном месте
чертежа, как отрезок, параллельный оси
X.
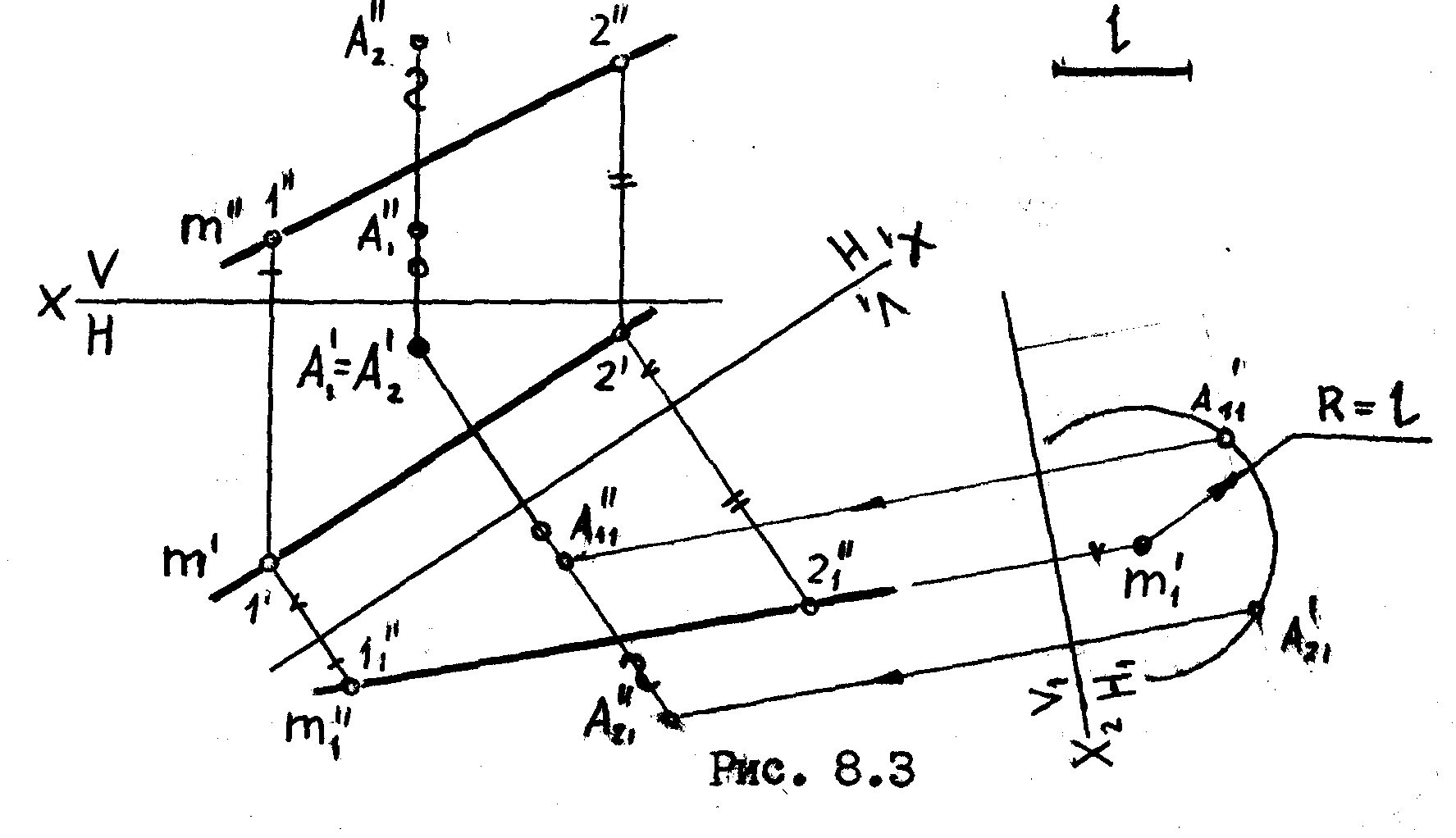
Задача
Дано: прямая m и горизонтальная проекция точки А. Построить фронтальную проекцию точки А, если известно расстояние от этой точки до прямой m, равное заданному отрезку 1 ,
8.4
Решение
Преобразуем
чертеж так, чтобы прямая m
стала проецирующей. На плоскости
, по отношению к которой прямая является
проецирующей, мы
будем
видеть в натуральную величину расстояние
точки А
до этой прямой. Проекция точки А
на плоскости
,
должна отстоять от прямой m
на расстоянии l
и от оси X2
, на том же расстоянии, что и точка
от оси Х1.
Этим условиям удовлетворяют точки
и
,т.е.
видим, что задача имеет два решения.
Имея проекции точек
и
,находим
искомые их фронтальные проекции
и
8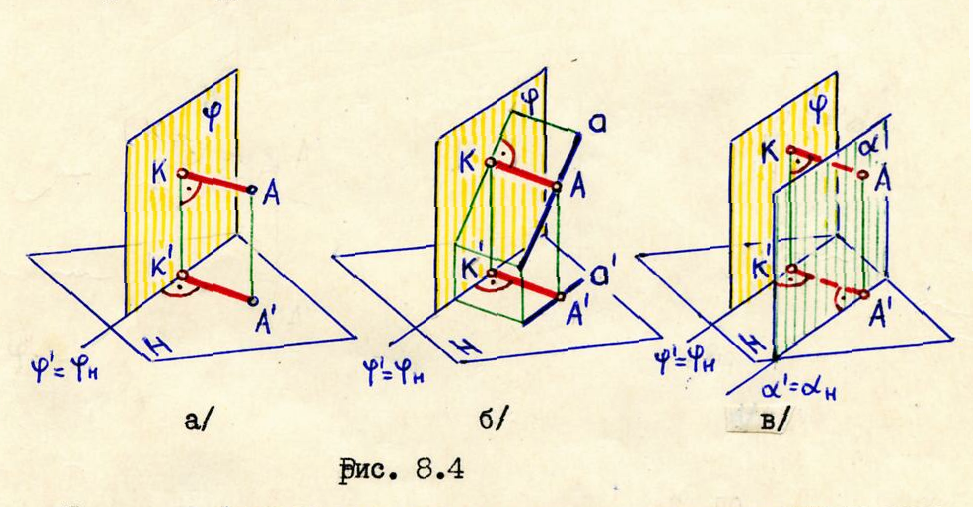
.3
Третья группа задач.
Из
рис, 8.4 мы видим, что расстояния,
определяемые в задачах тртьей группы
/задачи № 5,6,7/ будут проецироваться на
плоскость проекций в натуральную
величину в том случае, если плоскость
будет
проецирующей по отношению к этой
плоскости проекций.
Следовательно, для решения этой группы задач следует применить третью основную задачу на преобразование чертежа. Напомним, что третьей задачей на преобразование чертежа мы называем задачу преобразования плоскости общего положения в проецирующую.