
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Основные теоремы дифференциального исчисления
Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение.
Теорема
2 (Ролля).
Если функция y = f(x)
непрерывна на отрезке
 ,
дифференцируема на интервале (а, b)
и на концах отрезка принимает одинаковые
значения
,
дифференцируема на интервале (а, b)
и на концах отрезка принимает одинаковые
значения
 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка
 ,
в которой производная
,
в которой производная
 обращается
в нуль, т.е.
обращается
в нуль, т.е.
 .
.
Теорема
3 (Лагранжа).
Если функция y = f(x)
непрерывна на отрезке
 и дифференцируема на интервале (а, b),
то найдется хотя бы одна точка
и дифференцируема на интервале (а, b),
то найдется хотя бы одна точка
 ,
в которой выполняется равенство
,
в которой выполняется равенство

Теорема
4 (Коши).
Если функции
 и
и
 непрерывны на отрезке
непрерывны на отрезке
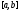 ,
дифференцируемы на
интервале (а, b),
причем
,
дифференцируемы на
интервале (а, b),
причем
 для
для
 ,
то найдется
хотя бы одна точка
,
то найдется
хотя бы одна точка
 такая,
что выполняется равенство
такая,
что выполняется равенство
 .
.
Раскрытие неопределенностей с помощью правила Лопиталя
Рассмотрим
способ раскрытия неопределенностей
вида
 и
и
 .
.
Теорема
5 (правило Лопиталя – Бернулли).
Если функции
 и
и
 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1)
определены и дифференцируемы на
интервале (а, b),
за исключением, быть может, точки
 ,
причем
,
причем
 и
и

 ;
;
2)
 ;
;
3) существует предел (конечный или бесконечный) отношения производных
 ;
;
тогда
существует также предел отношения
функций
 ,
причем
,
причем

Правило
Лопиталя справедливо и в случае
 .
.
Замечание.
Если отношение
 в
свою очередь представляет собой
неопределенность вида
в
свою очередь представляет собой
неопределенность вида
 или
или
 ,
и производные
,
и производные
 и
и
 удовлетворяют условиям теоремы, то
правило Лопиталя можно применить второй
раз, т. е.
удовлетворяют условиям теоремы, то
правило Лопиталя можно применить второй
раз, т. е.

Правило Лопиталя можно применять до тех пор, пока не будет получена дробь, для которой условия, предусмотренные теоремой, уже не выполняются.
Формула Тейлора
Пусть
функция f
имеет в некоторой окрестности точки
 производные
до n-го
порядка включительно.
Тогда
для любой точки х
из этой окрестности имеет место равенство:
производные
до n-го
порядка включительно.
Тогда
для любой точки х
из этой окрестности имеет место равенство:

где
 называется остаточным
членом.
В курсе математического анализа
доказывается, что
называется остаточным
членом.
В курсе математического анализа
доказывается, что
 .
Такой остаточный член
называется остаточным
членом в форме Пеано.
Тогда последнее равенство можно
переписать в виде:
.
Такой остаточный член
называется остаточным
членом в форме Пеано.
Тогда последнее равенство можно
переписать в виде:
 (11)
(11)
Полученная
формула разложения функции по степеням
 с остаточным членом в форме Пеано
называется формулой
Тейлора.
с остаточным членом в форме Пеано
называется формулой
Тейлора.
В
частности, при
 формула
(11) примет вид:
формула
(11) примет вид:
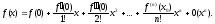 (12)
(12)
Формула разложения функции по степеням x с остаточным членом в форме Пеано называется формулой Маклорена.
Таким
образом, поведение любой n
раз
дифференцируемой функции в окрестности
точки
 (в
частности,
(в
частности,
 )
можно описать многочленом достаточно
точно, а при
)
можно описать многочленом достаточно
точно, а при
 со сколь угодно высокой степенью
точности.
со сколь угодно высокой степенью
точности.
Разложение по формуле Маклорена некоторых элементарных функций
Запишем разложение по формуле Маклорена некоторых элементарных функций:





Замечание.
Если в разложении функции
 положить
положить
 ,
где
,
где
 ,
то все члены этой формулы, начиная с
(n+1)-го,
исчезают, и формула Маклорена превращается
в формулу бинома Ньютона
,
то все члены этой формулы, начиная с
(n+1)-го,
исчезают, и формула Маклорена превращается
в формулу бинома Ньютона

Исследование функций с помощью производных Условия возрастания и убывания функции
Теорема
6 (об условии возрастания (убывания)
монотонной функции). Если
функция y = f(x)
дифференцируема на некотором интервале
(а,
b)
и
 (
( )
для
)
для
 ,
то эта функция возрастает (убывает) на
интервале (а,
b).
,
то эта функция возрастает (убывает) на
интервале (а,
b).
Доказательство.
Возьмем
точки
 из интервала (а,
b),
причем
из интервала (а,
b),
причем
 .
Для
функции y = f(x)
выполняются условия теоремы Лагранжа
на отрезке
.
Для
функции y = f(x)
выполняются условия теоремы Лагранжа
на отрезке
 ,
поэтому существует точка
,
поэтому существует точка
 ,
в которой
,
в которой

Проанализируем
полученное равенство: если
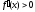 ,
то из неравенства
,
то из неравенства
 следует неравенство
следует неравенство
 ,
т. е. функция y = f(x)
на интервале (а,
b)
возрастает. Обратно:
если
,
т. е. функция y = f(x)
на интервале (а,
b)
возрастает. Обратно:
если
 ,
то из неравенства
,
то из неравенства
 следует неравенство
следует неравенство
 ,
т. е. функция y = f(x)
на интервале (а,
b)
убывает.
,
т. е. функция y = f(x)
на интервале (а,
b)
убывает.
