Дифференциальные уравнения второго порядка (основные понятия)

Дифференциальное уравнение второго порядка имеет вид:

(10)

Будем рассматривать уравнения, которые можно разрешить относительно 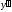, т. е. представить в виде

.

Для уравнения справедлива теорема, которая называется теоремой о существовании и единственности решения дифференциального уравнения второго порядка.

Теорема 2 (теорема Коши). Если в уравнении

функция и ее частные производныеи непрерывны в некоторой области D пространства переменных, содержащего некоторую точку , то существует единственное решение этого уравнения

,

удовлетворяющее условиям:

. (11)

Геометрический смысл теоремы заключается в том, что через заданную точку на координатной плоскости Oxy проходит единственная интегральная кривая с заданным угловым коэффициентом касательной.

Условия (11) называют начальными условиями, а задачу отыскания решения по заданным начальным условиям называют задачей Коши.

Определение 10. Общим решением уравнения называется функция , где – не зависящие от x произвольные постоянные, удовлетворяющие условиям:

1. является решением уравнения для каждого фиксированного значения ;

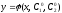2. каковы бы ни были начальные условия , существуют единственные значения постоянных такие, что функция является решением уравнения и удовлетворяет начальным условиям.

Определение 11. Всякое решение уравнения , получающегося из общего решения при конкретных значениях постоянных , называется частным решением.

Решения дифференциального уравнения , записанные в виде

назывются общим и частным интегралом соответственно.

Геометрически общее решение дифференциального уравнения представляет собой множество интегральных кривых; частное решение – одну интегральную кривую этого множества, проходящую через точку и имеющую в ней касательную с заданным угловым коэффициентом .

Уравнения, допускающие понижение порядка

Существует три вида уравнения , которые при помощи замены переменной (искомой функции) сводятся к уравнениям первого порядка.

1. Уравнения вида

(12)

Введем новую функцию p(x) путем замены . Тогда и получаем уравнение первого порядка . Решив его, т. е. найдя функцию p=p(x), решим затем уравнение Получим общее решение уравнения (12).

Замечание. На практике при решении уравнения (12) будем поступать иначе. Порядок в уравнении будем понижать непосредственно путем последовательного интегрирования данного уравнения.

2. Уравнения вида

(13)

т. е. уравнение, не содержащее явно искомой функции y.

Обозначим , где – новая неизвестная функция. Тогда и уравнение (13) принимает вид

.

Пусть – общее решение полученного дифференциального уравнения первого порядка. Сделав обратную замену , получаем . Для отыскания y достаточно проинтегрировать последнее уравнение. Общее решение уравнения (13) будет иметь вид

.

Частным случаем уравнения (13) является уравнение

не содержащее также и независимую переменную x. Оно интегрируется тем же способом:

. Получается уравнение с разделяющимися переменными.

3. Уравнения вида

(14)

т. е. уравнение, не содержащее независимой переменной x.

Для понижения порядка уравнения введем новую функцию , зависящую от переменной y, полагая . Дифференцируем это равенство по x, учитывая, что :

,

т. е. . После замены уравнение (14) запишется в виде:

Пусть – общее решение полученного дифференциального уравнения первого порядка. Сделав обратную замену , получаем – дифференциальное уравнение с разделяющимися переменными. Интегрируя его, найдем общий интеграл данного дифференциального уравнения

Частным случаем уравнения (14) является уравнение

.

Такое уравнение решается при помощи аналогичной подстановки .