Уравнения с разделяющимися переменными

Определение 6. Дифференциальное уравнение вида

(3)

где – непрерывные функции, называется уравнением с разделяющимися переменными.

Отметим, что правая часть уравнения представляет собой произведение, в которой один сомножитель зависит только от x, а другой – только от у. Метод решения такого вида уравнений носит название разделения переменных. Он состоит в следующем:

Умножим обе части уравнения (3) на dx и одновременно поделим обе его части на (предполагая, что ):

Считая y известной функцией от x, равенство 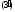можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным слагаемым. Интегрируя левую часть по y, а правую по x, получим:

Мы получили соотношение, связывающее решение у, независимую переменную x и произвольную постоянную С, т. е. получили общий интеграл уравнения (3).

Замечание. Уравнение вида приводится к уравнениям с разделяющимися переменными заменой .

Однородные дифференциальные уравнения

Определение 7. Функция 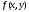называется однородной функцией степени n относительно переменных x и у, если при любом справедливо тождество

Определение 8. Уравнение первого порядка

(4)

называется однородным относительно x и y, если функция есть однородная функция нулевой степени относительно переменных x и у.

Замена т. е. y=ux приводит однородное уравнение к уравнению с разделяющимися переменными.

Замечание 1. Уравнение является однородным, если и однородные функции одной и той же степени. Это следует из того, что отношение двух однородных функций одной и той же степени является однородной функцией степени нуль.

Замечание 2. К однородным уравнениям приводятся уравнения вида . Это достигается линейной заменой , где – координаты очки пересечения прямых и . Если же указанные прямые не пересекаются, то в этом случае уравнение приводится к уравнению с разделяющимися переменными с помощью замены .

Линейные уравнения. Уравнения я. Бернулли

Определение 9. Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид

(5)

где , 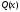– заданные непрерывные функции от x , в частности – постоянные.

Если 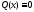, то уравнение (5) называется линейным однородным уравнением; если же функция не равна тождественно нулю, то уравнение (5) называется линейным неоднородным уравнением.

Метод вариации произвольной постоянной (метод Лагранжа). Рассмотрим однородное уравнение

Его общее решение имеет вид . Решение исходного уравнения (5) ищется в виде:

(6)

_{Подставляя (6) в (5), для определения} получим уравнение . Откуда

(7)

где С – произвольная постоянная. Подставляя из (7) в (6), находим общее решение уравнения (5):

(8)

Метод Бернулли. Решение уравнения (5) ищется в виде , где и – неизвестные функции от x, причем одна из них произвольна, но не равна нулю. Действительно, любую функцию можно представить в виде

Тогда . Подставляя y и в (5), имеем

или

Подберем так, чтобы выражение в скобках было равно нулю, т. е. решим уравнение . В виду свободы выбора функции , среди множества решений этого уравнения выберем решение . Тогда находим из уравнения

т. е. где С – произвольная постоянная. Перемножая и , находим решение (8).

Определение 10. Уравнением Бернулли называется уравнение вида

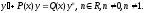(9)

При n=0 получаем линейное уравнение, при n=1 – уравнение с разделяющимися переменными.

Уравнение Бернулли можно привести к линейному уравнению заменой Однако на практике решения уравнения Бернулли удобней искать в виде , не приводя его к линейному уравнению.