6

ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ ПО МАТ АНАЛИЗУ

1. Множества. Операции над множествами.

ОПР1: Множество – совокупность определенных различных между собой объектов мыслимых как единое целое.

ОПР2: Если множества Х и У состоят из одних элементов, то они совпадают Х=У.

ОПР3: Если все элементы Х  У, то Х содержится в У, Х – подмножество У, Х У или У Х.

ОПР4: Если Х не содержится в У, Х У.

ОПР5: Пустое множество – множество, не содержащее элементов, подмножество любого множества - .

ОПР1: Пересечение А и В – С, состоящее из элементов, принадлежащих как А, так и В, АВ.

ОПР2: Объединение А и В – С, состоящее из элементов, принадлежащих хотя бы одному из А или В, АВ.

ОПР3: Разность А и В – С, состоящее из элементов А, не принадлежащих В, АВ.

ОРП4: Дополнение А – С, состоящее из элементов U, не принадлежащих А, А’.

2. Множество вещественных чисел. Свойства вещественных чисел.

ОПР1: Множество вещественных чисел состоит из рациональных и иррациональных чисел.

ОПР2: Рациональное число – число, которое можно представить в виде p/q, где p и q – целые числа, причем q0, любое целое число, конечная или периодическая бесконечная десятичная дробь.

ОПР3: Иррациональное число – число, которое не является рациональным, непериодическая бесконечная десятичная дробь.

ОПР4: Свойства вещественных чисел.

1. А+В = В+А.

2. А+(В+С) = (А+В)+С.

3. А*В = В*А.

4. А*(В*С) = (А*В)*С.

5. (А+В)*С = А*С+В*С.

6. Существует единственное число 0 такое, что А+0 =А для любого числа А.

7. Для любого числа А существует число (-А), что А+(-А) = 0.

8. Существует единственное число 1  0, что для любого числа А, А*1 = А.

9. Для любого числа А0, существует число 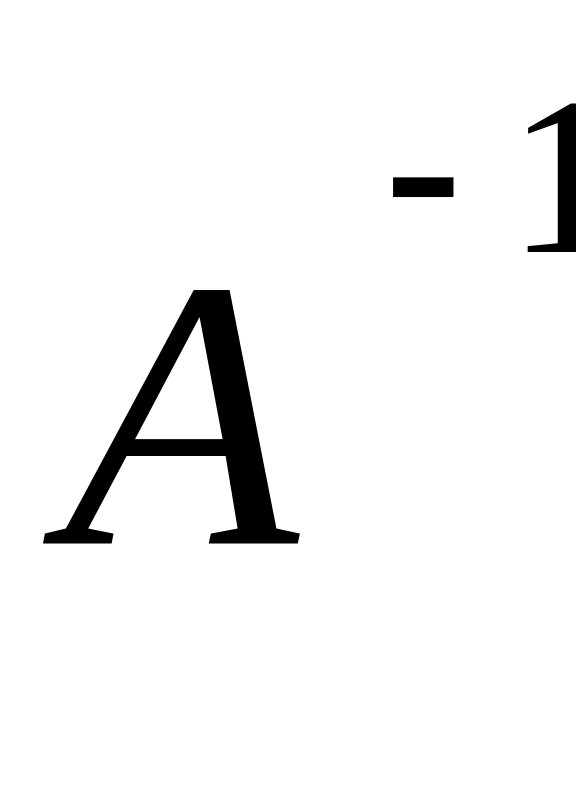, что А* = 1.

10. Если А>B и B>C, то B>C.

11. Если A>B, то A+C>B+C.

12. Если A>0 и B>0, то A*B>0.

13. Х и У – два множества, из вещественных чисел. Тогда, если для любых чисел х и у принадлежащих Х и У выполняется неравенство xy, то существует хотя бы одно число С такое, что для всех таких х и у выполняется xCy. (xX)(yY)(xy)(CR) : xCy

14. Число Х = В+(-А) является решением уравнения А+Х = В.

Док–во: По свойствам 1, 2, 6, 7 А+В+(-А)=В.

15. Число Х = В* - решение уравнения А*Х = В, если А0.

16. Если А<В, то –А>-В.

Док–во: Так как А<В, то В - А>0 В – А+(-В)>0+(-B)  -A>-B

17. Если А>В и С>D, то А+С>В+D.

18. Если А<В и С>D, то А-С<В-D.

19. A-A = 0.

20. A*0 = 0.

21. –(-A) = A.

22. (-A)*B = -A*B.

23. Если A<0 и B>0, то A*B<0.

24. Если A<0 и B<0, то A*B>0.

25. Если А0, то А*А = >0.

26. Если А>0, то >0.

3. Грани числовых множеств. Свойство точной грани.

ОПР1: Говорят, что множество Х ограничено сверху, если существует точка С такая, что для всех х из множества Х выполняется неравенство хC. (C)(xX): xC

ОПР2: Говорят, что множество Х ограничено снизу, если существует точка С такая, что для всех х из множества Х выполняется неравенство х С. (C)(xX):xC

ОПР3: Множество ограниченное сверху и снизу – ограниченное, если существуют точки M и m такие, что для всех х из множества Х выполняется неравенство mxM.

(m;M)(xX):mxM

ОПР4: Множество ограниченное сверху и снизу – ограниченное, если существуют точка А>0 такая, что для всех х из множества Х выполняется неравенство |x|A.

(A>0)(xX):|x|A

ТЕОР1: Ограниченное сверху множество имеет бесконечное множество верхних граней.

Док-во: Пусть С – верхняя грань множества Х  (C) (хХ): хC, произвольное C’>C  для хХ хС<C’  x<C’  C’ – верхняя грань множества Х хХ хС<C’  x<C’  Ограниченное сверху множество имеет бесконечное число верхних граней.

ТЕОР2: Ограниченное снизу множество имеет бесконечное множество нижних граней.

Док-во: Пусть С – нижняя грань множества Х  (C) (хХ): хC, произвольное C’<C  для хХ хС>C’  x>C’  C’ – нижняя грань множества Х хХ хС>C’  x>C’  Ограниченное снизу множество имеет бесконечное число нижних граней.

ОПР5: Наименьшая из верхних граней ограниченного сверху множества – точная верхняя грань.

ОПР6: Наибольшая из нижних граней ограниченного снизу множества - точная нижняя грань.

ТЕОР3: Свойство точной верхней грани.

Точную верхнюю грань нельзя уменьшить. Как бы не было мало  > 0, найдется х’, принадлежащий множеству Х, обладающий свойством х’>sup(x-  ). (>0)(x’X):x’>sup(x - )

Док–во: Пусть не существует x’X, обладающего свойством x’> sup(x) -   для всех хХ выполняется условие x<sup(x) - .

: не существует X’X x’>sup (x) -   (xX): x<sup (x) -   sup (x) -  - точная верхняя грань множества Х, это противоречит тому, что sup (x) – точная верхняя грань.

ТЕОР4: Свойство точной нижней грани.

Точную нижнюю грань нельзя увеличить. Как бы не было велико  >0, найдется х’, принадлежащий множеству Х, обладающий свойством х’<inf(x+). (>0)(x’X):x’>inf(x + )

Док–во: Пусть не существует x’X, обладающего свойством x’<inf(x) +   для всех хХ выполняется условие x>inf(x) + .

: не существует x’X x’<inf (x) +   (xX): x>inf(x) +   inf(x)+  - точная нижняя грань множества Х, это противоречит тому, что inf(x) – точная нижняя грань.