Теорема о непрерывной сложной функции.
ТЕОР: Пусть функции Z=(x) непрерывна в точке X0, а функция Y=f(z) непрерывна в точке Z0. Тогда сложная функция Y=f((x)) непрерывна в точке X0.
Док-во: Пусть Х1, Х2, Х3,…, Хn,… - последовательность из множества Х, сходится к точке Х0. Тогда в силу непрерывности функции Z=(x) в точке Х0 имеем lim Zn = lim (Xn) = (X0) = Z0 при n, то есть соответствующая последовательность точек Z1, Z2, Z3,…, Zn,… сходится к точке Z0. В силу непрерывности функции f(z) в точке Z0 имеем lim f(Zn) = f(Z0), т. е. lim f[(Xn)] = f[(X0)]. Получаем, что предел функции f((x)) в точке Х0 равен значению функции в точке Х0. Функция непрерывна.
Теорема о непрерывной обратной функции.
ТЕОР: Пусть функция Y=f(x) определена, строго монотонна и непрерывна на некотором промежутке Х и пусть У – множество ее значений. Тогда на множестве У обратная функция X=(y) однозначна, строго монотонна и непрерывна.
ЗАМ: если обратная функция X=(y) однозначна, то, очевидно, что f – обратная функция для функции , говорят, что f и – взаимообратные.
Понятие производной.
ОПР1: Приращением функции Y=f(x) в точке X0, отвечающим приращению аргумента X, будем называть число Y=f(X0+X) – f(X0).
ОПР2: Производной функции Y=f(x) в данной точке X0 называется предел при X0 отношения приращения функции к приращению аргумента. При условии, что он существует – конечная производная. Если он равен бесконечности, то функция имеет бесконечную производную. Если функция имеет конечную производную в каждой точке множества Х, то можно рассматривать производную как функцию определенную на множестве Х.
Геометрический смысл производной.
Пусть функция Y=f(x) определена на интервале (a, b) и пусть точка А на графике функции соответствует значению аргумента Х0, а точка В – значению (Х0+Х). Проведем через А и В прямую и назовем ее секущей. Обозначим через (Х) угол между секущей и осью ОХ.
ОПР1: Если при Х0 существует lim (X)= 0, то прямую с угловым коэффициентом К=tg 0, проходящим через точку А(Х0, f(X0)), называют предельным положением секущей АВ при Х0 (или ВА).
ОПР2: Касательной S к графику функции Y=f(x) в точке А будем называть предельное положение секущей АВ при Х0 (или при ВА).
ТЕОР1: Если функция Y=f(x) имеет в точке Х0 производную, то существует касательная к графику Y=f(x) в точке М(X0, f(X0)), угловой коэффициент касательной K=tg 0 = f ’(X0).
Д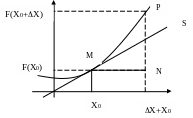
ок-во:
Проведем прямую MN
|| OX,
тогда PN
|| OY,
MN=X,
PN=Y,
PMN=
tg
(X)
= Y/X
=
(X)
=arctg
Y/X.
Перейдем к пределу при X0.
Так как существует производная f
’(X0),
то существует и предел lim
Y/X=f
’(X0)
и так как функция arctg
Y/X
непрерывна
существует предел правой части
равенства:
lim arctg Y/X= arctg (lim Y/X)=arctg f ’(X0). Существует предел и левой части равенства. Получаем lim (X) = arctg f ’(X0). Существует предельное положение секущей РМ, т. е. существует касательная к графику функции Y=f(x) в точке А(X0, f(X0)), причем угол наклона этой касательной к оси ОХ равен arctg f ’(X0) и, значит, угловой коэффициент касательной tg 0= f ’(X0).
ОПР3: Составим уравнение касательной к графику функции Y=f(x) в точке A(X0, f(X0)). Уравнение прямой, проходящей через точку C(a, b) с угловым коэффициентом k имеет вид Y=b+k(x –a). Но в точке А значение функции равно f(X0), поэтому в уравнении а=Х0, b= f(X0), k= f ’(X0). Получаем уравнение касательной Y= f(X0)+ f ’(X0)(X - X0).
ОПР4: Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной в этой точке.