5. Методические указания к выполнению лабораторных работ

Лабораторная работа 1

Интерполяция функций с равноотстоящими узлами

методом Ньютона

1. Цель работы

Нахождение аналитического выражения функции, заданной таблицей, используя первую интерполяционную формулу Ньютона.

2. Основные теоретические положения

Для проверки правильности вычислений конечных разностей удобно использовать их свойство: сумма чисел в каждом столбце разностей равна разности крайних членов предыдущего столбца. Сумма всех разностей первого порядка определяется следующим образом:

(1)

Например, для n = 5: (y₁ + y₂ + y₃ + y₄ + y₅) – (y₀ + y₁ + y₂ + y₃ + y₄) = y₅ - y₀.

Аналогично, для разностей других порядков будем иметь:

(2)

Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции

Вычисление значений функции для значений аргументов, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона. В этом случае интерполяционный многочлен представляют в виде:

F(x) = P_n(x) = a₀ + a₁(x – x₀) + a₂(x –x₀)(x – x₁) +

+ a₃(x –x₀)(x- x₁)(x-x₂) + ... + a_n(x –x₀)(x- x₁)(x-x₂)…(x –x_n-1), (3)

при этом неизвестные значения коэффициентов a₀, a₁, a₂, …, a_n вычисляют по формуле

(i = 0, 1, 2, …, n), (4)

то есть

при i = 0 , [0!=1, Δ⁰y₀ = y₀],

при i = 1 = ,

при i = 2 = , и т. д.

Обратите внимание, что . (5)

После подстановки найденных коэффициентов a_i в выражение (3), получают первую интерполяционную формулу Ньютона:

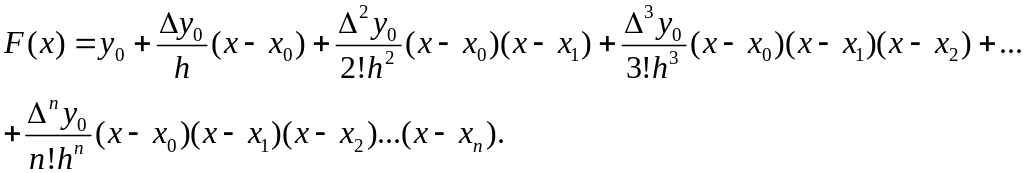( 6)

Пример.

Используя первую интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции, заданной таблицей (табл. 1). При составлении таблицы конечных разностей контролировать правильность вычислений.

Таблица 1

xi	yi
0	8,5
1	10,5
2	12,0
3	13,5
4	14,5
5	15,5

Решение.

□Степень многочлена определяется порядком конечных разностей, т.е. для рассматриваемого примера интерполяционный многочлен будет иметь вид

F(x) = P_n(x) = a₀ + a₁(x – x₀) + a₂(x –x₀)(x – x₁) + a₃(x –x₀)(x- x₁)(x-x₂) +

+ a₄(x –x₀)(x- x₁)(x-x₂)(x –x₃) + a₅(x –x₀)(x- x₁)(x-x₂)(x –x₃) (x-x₄) (7)

или

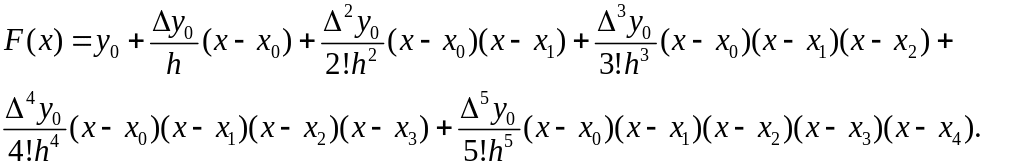(8)

Вычисление конечных разностей, значений коэффициентов интерполяционного многочлена (особенно высокого порядка), а также значений функции для заданных значений аргументов удобно выполнять в электронной таблице (рис. 1), так как «вручную» выполнять подобные вычисления долго и утомительно.

Режим вычислений

Рис. 1

В верхнюю часть таблицы следует ввести исходные данные: значение шага интерполяции h, который по условию равен 1, значения аргумента x и соответствующие им значения функции f(x), а также значение аргумента x = 2,5, для которого требуется вычислить значение заданной функции, с помощью построенного интерполяционного многочлена.

Реализация вычисления конечных разностей выполняется, как показано в таблице. Значения конечных разностей и значение f(x₀), которые будут использованы в вычислениях по формуле (2), выделены в таблице полужирным начертанием. Правильность полученных конечных разностей подтверждают результаты вычислений, выполненные по формуле (2) (в ячейках D11 и С12, Е11 и D12 и т.д.).

Вычисление коэффициентов интерполяционной формулы (7) целесообразно выполнять, используя свойство (5)

,

а именно:

i = 0

i = 1

i = 2 (9)

i = 3

I = 4

i = 5 = .

Для этого в блоке ячеек В16:В20 реализовано вычисление промежуточных значений коэффициентов таким образом, чтобы каждый последующий элемент столбца получался из предыдущего, умножением на . Это позволит при необходимости легко настраивать полученную таблицу на решение задач любой размерности.

В блоке ячеек D16:D20 вычисляются значения коэффициентов интерполяционного многочлена a₀, a₁, …, a₅ (8), путем умножения значений f(x₀), и конечных разностей, полученных в блоке С5: H5 на соответствующие им значения промежуточных коэффициентов (В16:В20).

В соответствии с (7), каждый коэффициент a₁, a₂, a₃, a₄, a₅ соответственно требуется умножить на (x –x₀), (x –x₀)(x- x₁), (x –x₀)(x- x₁)(x-x₂), (x –x₀)(x- x₁)(x-x₂)(x –x₃) (x-x₄). Поэтому в блоке ячеек I5: I10 предусмотрено вычисление значений (x-x_i), которые затем используются для вычисления их произведений в блоке Н16:Н20, причем каждый последующий элемент получается из предыдущего.

В блоке ячеек I15: I20 выполняется вычисление значений каждого члена интерполяционного многочлена, просуммировав которые получается значение интерполяционного многочлена для x = 2,5.

Таким образом, получено выражение интерполяционного многочлена:

F(x) = P₅(x) = 8,5 + 2(x-0) - 0,25(x-0)(x-1) + 0,08(x-0)(x-1)(x-2) –

-0,04(x-0)(x-1)(x-2)(x-3) + 0,02(x-0)(x-1)(x-2)(x-3)(x-4). (10)

Коэффициенты многочлена, полученные при ручном счете по формуле (9), совпадают со значениям коэффициентов, полученными в Excel (см. столбец D15:D20).

Значение F(2,5) = 12,78 (получено в ячейке I21). Подставив значение x = 2,5 в (10), получим:

F(2,5) = P₅(2,5) = 8,5 + 2(2,5-0) - 0,25(2,5-0)(2,5-1) + 0,08(2,5-0)(2,5-1)(2,5-2) –

-0,04(2,5-0)(2,5-1)(2,5-2)(2,5-3)+0,02(2,5-0)(2,5-1)(2,5-2)(2,5-3)(2,5-4) = 12,78.

Значение F(x) при x = 2,5 при ручном счете и вычислениями в Excel совпадают.

На рис. 2 показана таблица, представленная в режиме формул, в которой алгоритм описанных вычислений становится более наглядным.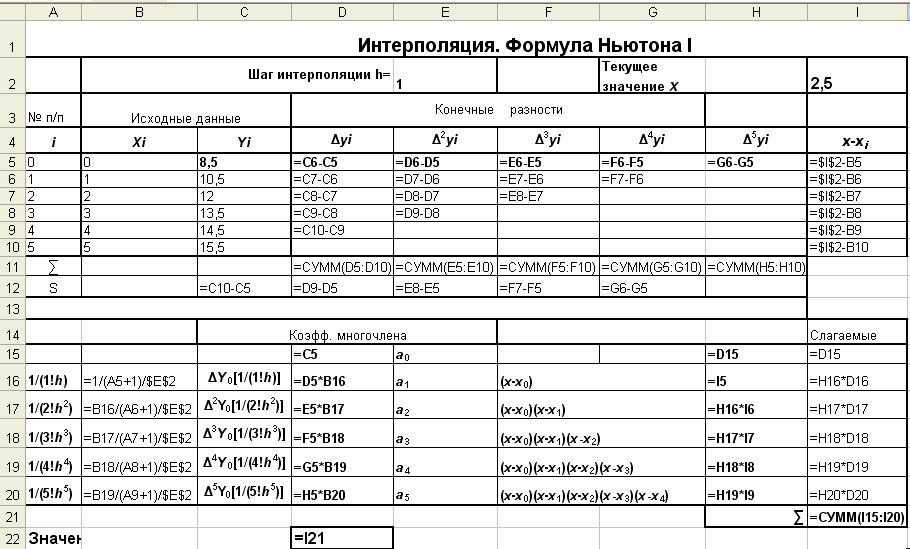

Режим формул

Р ис. 2.

При использовании электронных таблиц не представляет сложности вычисление значений многочлена для других значений х. Для этого достаточно в ячейке I2 изменить значение х, и мгновенно получим новое значение многочлена. Так же быстро можно изменить исходные значения аргумента х и соответствующие им значения функции y. Для этого в блоки ячеек В5:В10 и С5:С10 – следует ввести новые значения.

Заполнять таблицу тоже достаточно просто, если разумно использовать абсолютную и относительную адресацию ячеек, на которые делаются ссылки в формулах, т.е. применять автозаполнение столбцов и строк. Настроить таблицу на построение многочленов более высоких порядков тоже не сложно, вставив в нужном месте нужное количество строк и столбцов и заполнить нужные ячейки автозаполнением.■

3. Порядок выполнения работы

Задание

1. Выполнить решение примера индивидуального контрольного задания по шести первым точкам (с.77), используя первую интерполяционную формулу Ньютона.

1.4. Реализовать вычисление коэффициентов интерполяционного многочлена средствами MS Excel.

Лабораторная работа 2

Приближенное решение уравнений.

Отделение корней. Уточнение корней методом касательных.

1. Цель работы

Ознакомление с численными методами решения конечных уравнений.

2. Основные теоретические положения

Пусть дано уравнение f(x) = 0, где f(x) – непрерывная функция на некотором отрезке. Корни этого уравнения x*– те значения аргумента x, которые обращают уравнение в тождество. Найти приближенное значение корня x* с точностью ε означает указать интервал длиной не более ε, содержащий значение корня x.

При отыскании приближенных значений корней уравнения приходится решать две задачи:

1) отделение корней, т.е. выделение интервалов из области непрерывности функции, в каждом из которых заключен только один корень уравнения;

2) уточнение корня, т.е. построение итерационного процесса, позволяющего сузить границы выделенного интервала до значения заданной точности.