2.2. Метод трапеций

Для получения формулы трапеций интервал интегрирования [a, b] разбивается на n подынтервалов равной длины (шагов) точками: x₀ = a, x₁, x₂, … , x_i, x_i+1, … , x_n = b так, что

x_i+1 - x_i = h = , i = 1, 2, …, n.

На каждом отрезке (x_i, x_i+1) дугу X_i X_i+1 графика подынтегральной функции y = f(x) заменяют стягивающей ее хордой (рис. 2.5) и вычисляют площади трапеций x_iX_i X_i+1x_i+1, высота которых равна h, а основания определяются значением функции f(x_i), f(x_i+1).

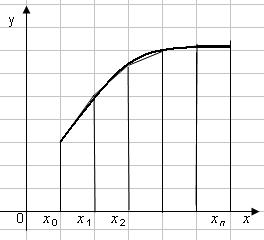
Рис. 2.5

Так как площадь трапеции равняется полусумме оснований, умноженной на высоту, интеграл приближенно равен сумме площадей всех полученных трапеций:

=

= =

= [f(x₀) + 2f(x₁) + 2f(x₂)+…+ + 2f(x_n-1) + f(x_n)]=

= [f(x_a) + 2f(x₁) + 2f(x₂)+…+ + 2f(x_n-1) + f(x_b)]=

= [ f(x_a) + f(x_b) + ]. (7)

Таким образом, формула трапеций имеет вид:

I = ≈ 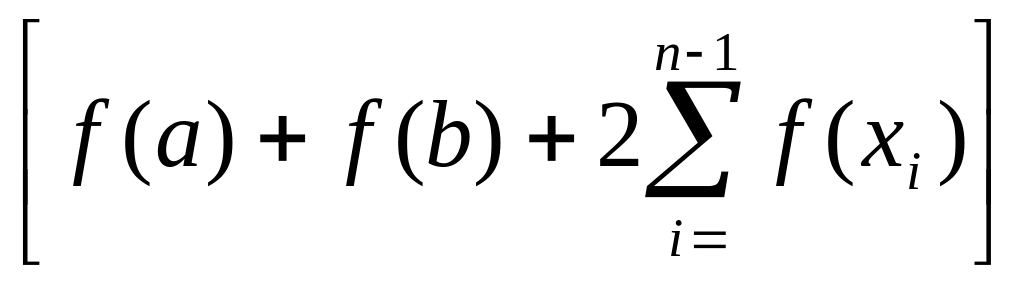. (8)

Точность интегрирования для этого метода приближенно равняется ε ≈ h².

Пример (продолжение). □Пользуясь формулой трапеций, вычислить при h = 0,2.

Решение. Вычисление интеграла методом трапеций (8) выполним в таблице Excel (рис. 6, 6-а).

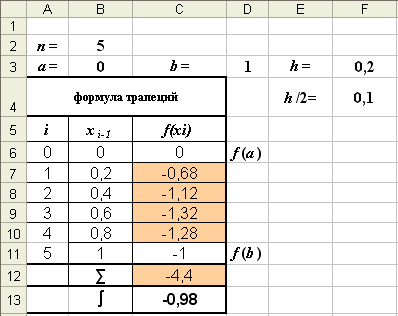
Режим решения

Рис. 6

∑ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1·[(0-1)-2·4,4] = -0,98

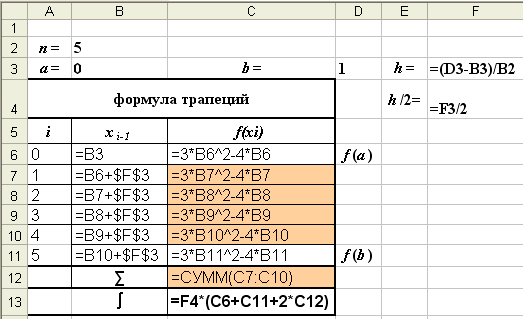
Режим показа формул

Рис. 6 - а

Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 7).

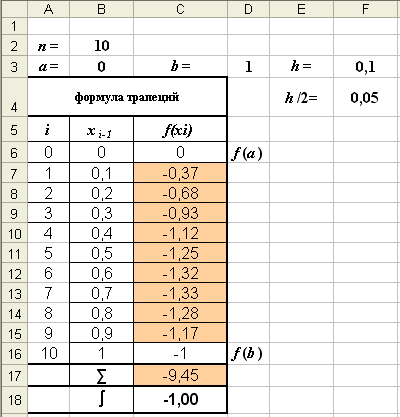
Рис. 7

∑ = -0,37 -0,68 -0,93 -1,12 -1,25 -1,32 -1,33 -1,28 -1,17 = -9,45

I = 0,05∙ [(0 -1) + 2∙(-9,45) = -1,00■

2.3. Метод парабол (Симпсона)

Для получения формулы парабол функция f(x) на интервале (x_i, x_i+1) заменяется параболой, проходящей через три точки кривой с абсциссами

x_i, (x_i +x_i+1)/2, x_i+1 (x_i, x_i+h, x_i+2h) (рис. 2.8).

Весь интервал интегрирования при этом разбивается на четное число отрезков (n = 2m).

Рис. 8

Формула парабол имеет вид:

I = ≈

Пример. □Пользуясь формулой парабол, вычислить при n = 10.

Решение.

h = Вычисление интеграла выполним в таблице Excel (рис. 9, 9-а).

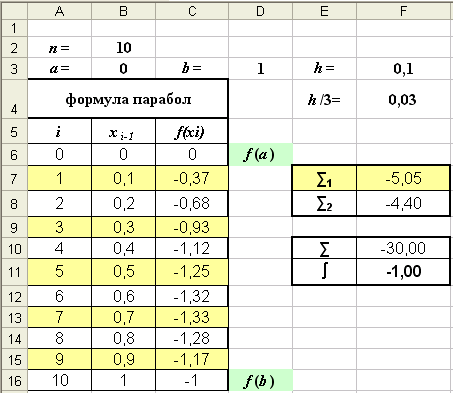
Режим решения

Рис. 9

∑₁ = -0,37- 0,93-1,25-1,32-1,17 = -5,05 ∑₂ = -0,68 -1,12 -1,32-1,28 = -4,4

∑ = (0- 1) + 4·(-5,05) +2·(-4,4) = -30,00 ∫ = 0,033 · (-30) = 1.■

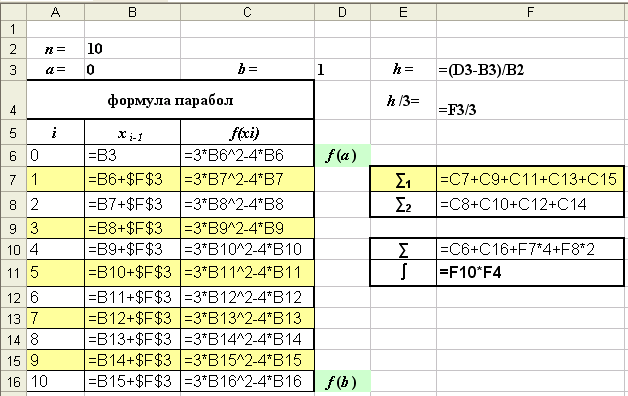
Режим формул

Рис. 9 - а

3. Порядок выполнения работы

1. Вычислить интеграл индивидуального задания всеми описанными методами в Excel с числом шагов, равным 5. При реализации решения в Excel увеличить число шагов в два раза, в три раза. Сравнить результаты вычислений, полученные при использовании данных методов с точным решением.

Лабораторная работа 5

Решение дифференциальных уравнений методом Эйлера

1. Цель работы

Изучение метода Эйлера для интегрирования дифференциальных уравнений.

2. Основные теоретические положения

Решить дифференциальное уравнение y' = f(x, y) численным методом –значит для заданной последовательности аргументов x₀, x₁, …, x_n и числа y₀, не определяя функцию y = F(x), найти такие значения у₁, у₂, …, y_n, что y_i = F(x_i) (i = 1, 2, …, n) и F(x₀) = y₀. Другими словами, численные методы позволяют вместо нахождения функции y = F(x), получить таблицу значений этой функции для заданной последовательности аргументов. Величина h = x_k – x_k-1 называется шагом интегрирования.

Для решения данной задачи используются различные численные методы, среди которых наиболее простым является метод Эйлера.

Пусть дано дифференциальное уравнение первого порядка

y' = f(x, y) (1)

с начальными условиями

x = x₀, у(x₀) = y₀.

Требуется найти решение уравнения (1) на отрезке [a, b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность x₀, x₁, …, x_n, где x_i = x₀ + i·h (i = 1, 2, …, n), а h = (b – a)/n – шаг сетки. Величина h = ∆ x_m = x_m+1 - x_i обычно выбирается постоянной и достаточно малой. При численном решении задачи вычисляются приближенные значения y_i (x_i) ≈ y_i в узлах сетки x_i (i = 1, 2, …, n).

Идея метода состоит в том, что при малом шаге сетки h производная искомой функции y'(x_i) может быть приближенно заменена конечными разностями

(2)

где y_i – значение функции в узле x_i.

Тогда y'(x_i)∙h = y_i+1 - y_i, отсюда y_i+1 = y_i+ y'(x_i)∙h, а, так как y'(x_i) = f(x_i, y_i), то

y_i+1 = y_i + h·f(x_i,y_i). (3)

Т.е. на каждом отрезке [x_i, x_i+1] выражение (1) можно заменить приближенным выражением (3).

Зная начальное значение y₀, и используя соотношение (3), можно последовательно от узла x_i к узлу x_i+1 определить все искомые значения y_i+1.

На практике, как правило, применяют «двойной просчет». Сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2 и

т.д.

Для достижения требуемой точности ε численного решения необходимо выполнение условия: |y_2n - y_n| < ε.

Пример 1. Используя метод Эйлера, составить на отрезке [0, 1] таблицу значений решения дифференциального уравнения

с начальными условиями x₀ = 0, y₀ = 1, выбрав шаг h = 0,2.

□Решение.

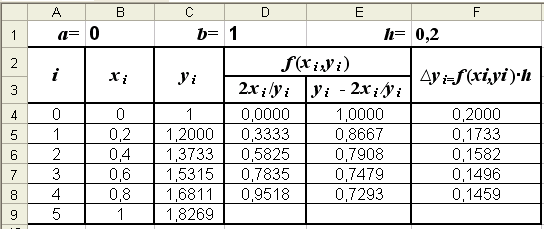
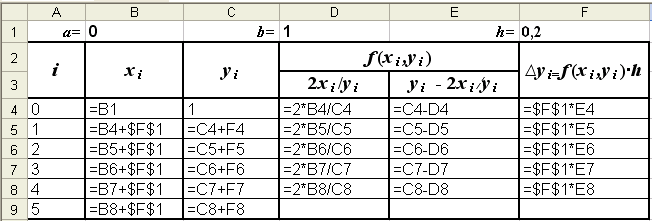
Результаты вычислений представим в таблице Excel (рис.1). Заполняется она следующим образом:

1) В первую строку, соответствующую значению i = 0, запишем начальные условия: x₀ = 0, y₀ = 1. По ним вычислим значение f(x₀, y₀):

а затем значение ∆y₀. Из (2) и (1) имеем

∆y₀ = y'(x₀)∙ ∆x₀ = y'(x₀)∙h = f(x₀, y₀) ∙h,

следовательно, ∆y₀ = h∙f(x₀, y₀) = 0,2∙1 = 0,2. Отсюда по формуле (3) для i = 0 получим

y₁ = y₀ + h∙f(x₀, y₀) = y₀+ ∆y₀ = 1 + 0,2 = 1,2.

2) Значение x₁ = x₀ + h = 0 + 0,2 = 0,2 и соответствующее ему значение y₁ =1,2 запишем во вторую строку таблицы, соответствующую i = 1.

Для x₁ = 0,2 и y₁ = 1,2 вычислим f(x₁, y₁).

Затем вычислим ∆y₁ = h∙f(x₁, y₁) = 0,2∙0,8667 = 0,1733.

Тогда по формуле (3) для i = 1 получим

y₂ = y₁ + h∙f(x₁, y₁) = y₁+ ∆y₁ = 1,2 + 0,1733 = 1, 3733.

3) Значения x₂ = x₁ + h = 0,2 + 0,2 = 0,4 и соответствующее ему значение y₂ =1,3733 запишем в третью строку таблицы (i = 2).

Аналогично следует выполнить вычисления для i = 2, 3, 4, 5 (см. рис. 1).■

Режим формул

Режим решения

Рис. 1

Метод Эйлера легко распространяется на решение дифференциальных уравнений высших порядков. Для этого такое дифференциальное уравнение надо предварительно привести к дифференциальному уравнению первого порядка.

Пусть дано дифференциальное уравнение

y'' = f(x, y, y') (4)

с начальными условиями

x = x₀, у(x₀) = y₀, у'(x₀) = y'₀.

Требуется найти решение уравнения (4) на отрезке [a, b].

С помощью подстановки y' = z, y'' = z' заменим уравнение (4) системой уравнений

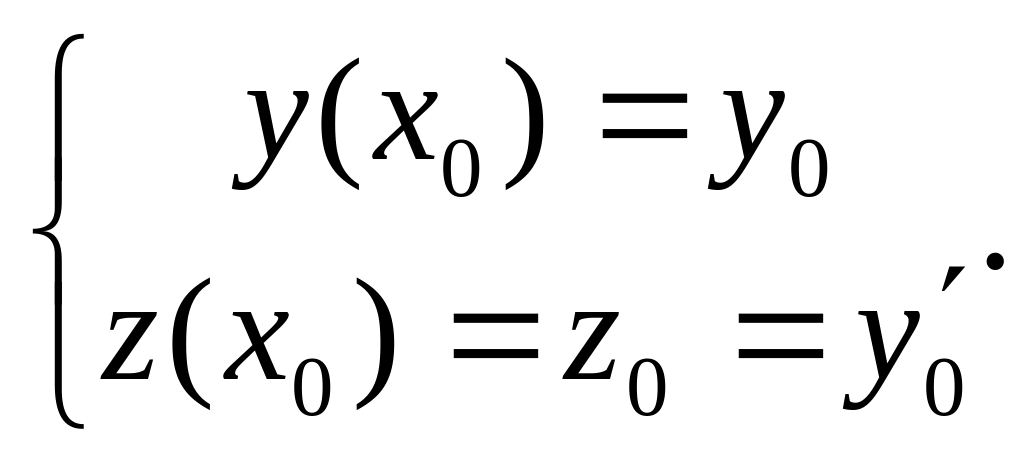и (5)

Таким образом, f₁(x, y, z) = z, f₂(x, y, z) = f(x, y, z) и задачу можно записать в общем виде:

и (6)

Аналогично можно свести к системе дифференциальных уравнений и уравнения более высокого порядка.

Пример 2. Используя метод Эйлера, составить на отрезке [1; 1,5] таблицу значений решения дифференциального уравнения

(7)

с начальными условиями y = 0,77, y' = -0,44 и выбрав шаг h = 0,1.

□Решение. С помощью подстановки y' = z, y'' = z' заменим уравнение (7) системой уравнений

y' = z,

с начальными условиями y₀(1) = 0,77 и z₀ = -0,44.

Таким образом,

f₁(x, y, z) = z, f₂(x, y, z) =

Результаты вычислений по формулам (6) запишем в таблице Excel (рис. 2). Заполняется она следующим образом:

в первую строку i = 0 запишем начальные условия: x₀ = 1,0, y₀ = 0,77, z₀ = -0,44.

Используя их, вычислим

f₁₀(x₀, y₀, z₀) = z₀ = -0,44,

f₂₀(x₀, y₀, z₀) =

а затем

∆y₀ = h∙f₁₀ = 0,1∙(-0,44) = -0,044, y₁ = y₀ + ∆y₁ = 0,77 + (-0,044) = 0,726,

∆z₀ = h∙f₂₀ = 0,1∙(-0,33) = -0,033, z₁ = z₀ + ∆z₁ = -0,44 + (-0,033) = -0,473.

Таким образом, во вторую строку таблицы, соответствующую i = 1, можно записать:

y₁ = 0,726, z₁ = -0,473.

По этим значениям можно вычислить

f₁₁(x₁, y₁, z₁) = z₁ = -0,473,

f₂₁(x₁, y₁, z₁) =

а затем

∆y₁ = h∙f₁₁ = 0,1∙(-0,473) = -0,047, y₂ = y₁ + ∆y₁ = 0,726 + (-0,047) = 0,679,

∆z₁ = h∙f₂₁ = 0,1∙(-0,296) = -0,030, z₂ = z₁ + ∆z₁ = -0,473 + (-0,030) =-0,503.

Аналогично следует выполнять вычисления для i = 2, 3, 4, 5 (см. рис. 2).■

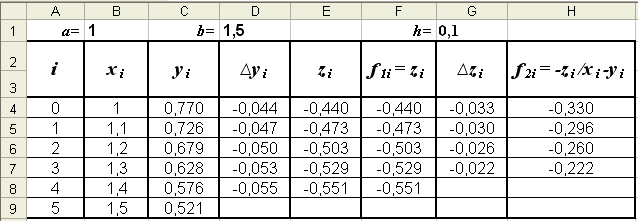
Режим формул

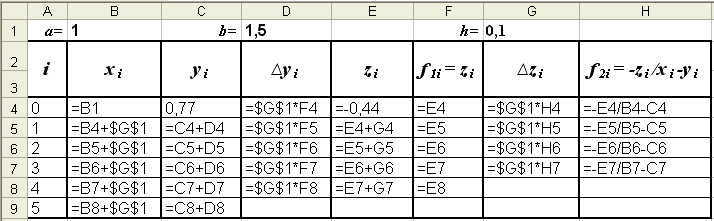
Режим решения

Рис. 2