2.1. Отделение корней Графический метод отделения корней

При графическом методе можно построить график функции для уравнения вида f(x) = 0. Значения действительных корней уравнения являются абсциссами точек пересечения функции y = f(x) с осью х.

Пример. Отделить корни уравнения x³ - 8x + 2 = 0 графическим методом, где x [-3, 3].

Решение.

□Для отделения корней можно построить график функции y = x³ -8 x + 2 (рис. 1), задав шаг изменения аргумента, например, равным 1. График удобно строить средствами Excel, используя Мастер диаграмм. Значениями действительных корней уравнения являются точки пересечения графика функции с осью x. Из графика видно, что корни находятся на интервалах [-3; -2], [0; 1] и [2; 3]. Если задать шаг изменения аргумента меньше выбранного, можно сузить границы интервалов.■

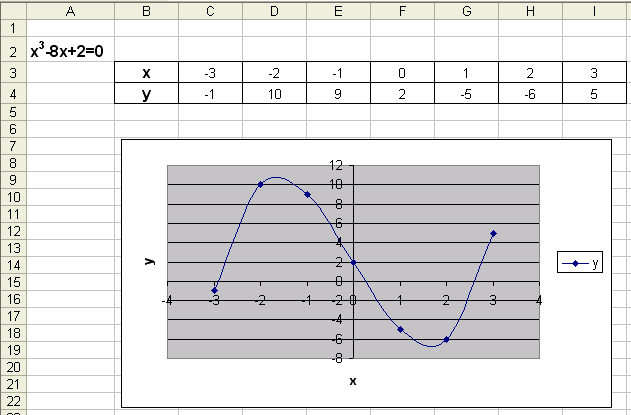
Рис. 1

Аналитический метод отделения корней

Для отделения действительных корней непрерывных функций следует помнить следующее:

• если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] одинаковые знаки (т.е. f(a)·f(b) > 0), то на этом интервале имеется четное число корней или их нет (рис. 2);

! нельзя забывать, что корнем функции может быть не только точка пересечения графика функции f(x) с осью x, но и его касание с осью x (рис. 3). В этом случае монотонность функции нарушается.

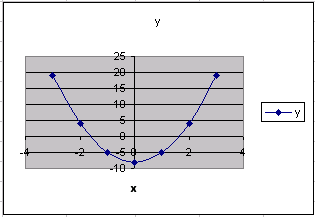
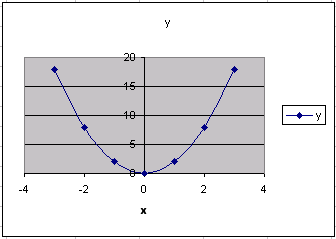
Рис. 2 Рис. 3

• если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] разные знаки (т.е. f(a)·f(b) < 0), то на этом интервале имеется нечетное число корней (рис. 4, 5);

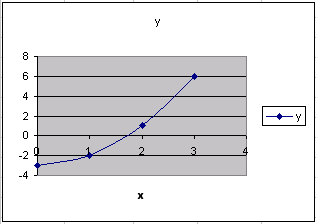
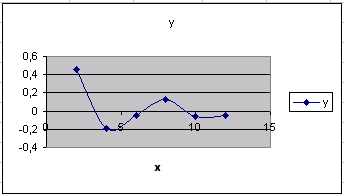
Рис. 4 Рис. 5

! Разные знаки функции на концах интервала указывают на наличие корня на интервале [a, b], но не гарантируют его единственности.

• если функция f(x) непрерывна на интервале [a, b], монотонна и ее значения на концах интервала имеют разные знаки (f(a)·f(b) < 0), то уравнение на этом интервале имеет единственный корень.

Из этого следует, что для единственности корня на участке [a, b] достаточно, чтобы выполнялись условия: f(a)·f(b) < 0, а f'(x) была знакопостоянна для любого x, принадлежащего [a, b].

! иногда для единственности корня бывает достаточно и знакопостоянства второй производной.

Таким образом, чтобы отделить все корни уравнения, следует:

• найти промежуток, где f(a)·f(b) < 0, а f'(x) или f''(x), или и f'(x), и f''(x), были знакопостоянны;

• отыскать нули и точки разрыва f'(x) и проверить, не являются ли они корнями уравнения.

Пример (продолжение). □Отделить все действительные корни уравнения f(x) = 0 на отрезке [-3, 3]:

f(x) = x³ - 8x +2 = 0.

Решение.

Вычислим значения функции f(x) на концах отрезка [-3, 3]:

f(-3) = (-3)³ - 8·(-3) + 2 = -1, f(3) = (3)³ - 8·3 + 2 = 5.

f(-3)∙f(3) < 0, поэтому на отрезке [-3, 3] имеется или один корень, или нечетное число корней.

f'(x) = 3x² - 8 – непрерывна. Для определения интервалов монотонности f(x) найдем значения x, при которых f'(x) = 0. f'(x) = 3x² – 8 = 0 при x = ≈ ±1,633.

Таким образом, можно отделить следующие интервалы монотонности функции f(x): [-3; -1,633], [-1,633; 1,633], [1,633; 3] и на каждом из этих интервалов отделено по одному корню уравнения.

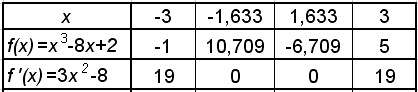
Для наглядности вычислим значения f(x) и f'(x) на концах этих промежутков (табл. 1). f'(x) = 3x² – 8.

Таблица 1