57)Определенный интеграл, как ф-ция верхнего предела.

Пусть в определенном интеграле, нижний предел a постоянен, а верхний b меняется, т.е. интеграл есть ф-ция верхнего предела. Обозначим верхний предел за х, а тогда переменную интегрирования за t. Полученную ф-цию обозначим за Ф(x):

(1)

Если f(t) неотрицательна то Ф(t) численно равна площади криволинейной трапеции.

Найдем производную от Ф(t), т.е. найдем производную определенного интеграла по верхнему пределу.

Теорема: Если f(x) непрерывная ф-ция и (1) то имеет место равенство:

56)Вычисление определенного интеграла. Формула Ньютона-Лейбница.

Пусть функция интегрирована на закрытом промежутке, тогда она интегрируема от 0 до [a,b], рассмотрим

Отметим, что обладает свойствами, если функция непрерывна на [a,b], то для F(x) имеет место следующее равенство (1)

Док-во дадим аргументу xx определим ( x+x )=

По теореме о среднем имеем f()x,[x;x+x]

Найдем придел что и (1)

Замечание равенство (1), показывает, что для функции на отрезке [a,b] , всегда есть первообразная , с переменным верхнем пределом.

Теорема: Если F(x) есть какая-либо первообразная от непрерывной ф-ции f(x), то справедлива формула:

58)Замена переменной в определенном интеграле.

Теорема: Пусть дан интеграл f(x) от a до b, где ф-ция f(x) непрерывна на отрезке [a,b]. Введем новую переменную t по формуле x= (x), такая что если: ( )=a, ( )=b,

(t) и ’(t) непрерывны на отрезке [a,b], f[ (t)] определены и непрерывны на [a,b], то:

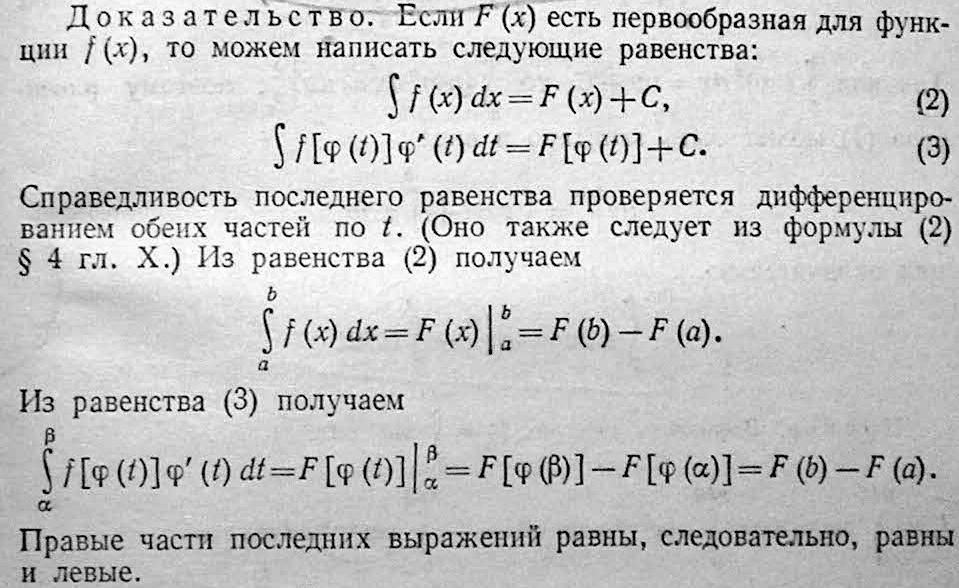
Замечание: при замене не нужно возвращаться к первоначальным переменным.

Интегрирование по частям.

59)Вычисление площадей в прямоугольной системе координат.

Пусть ф-ция f(x) определена на [a,b], то как известно площадь криволинейной трапеции

* если f(x)>=0 равна: интегралу от a до b.

* если f(x)<0 то интеграл <0, тогда мы берем его по модулю, либо со знаком -.

* если же ф-ция меняет свой знак конечное кол-во раз, то мы разбиваем ее на участки и берем интеграл соответствующих участков по правилам выше стоящим.

* если имеем две ф-ции и нужно вычислить площадь ограниченной ими, то мы вычисляем интеграл от разности большей и меньшей ф-ции.

* если ф-ции пересекаются конечное кол-во раз то мы разбиваем на участки и проделываем те же действия.

60)Вычисление площади криволинейной трапеции для кривой заданной параметрически.

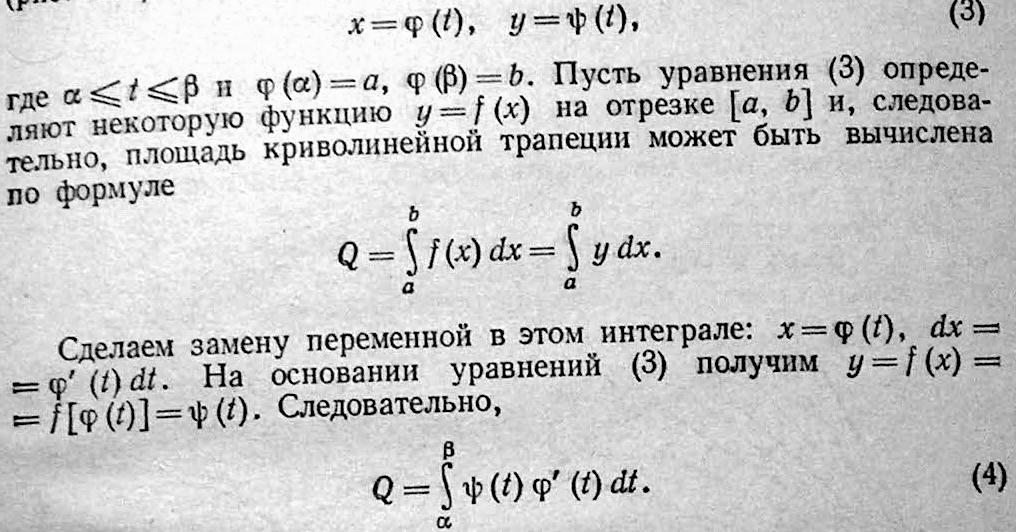
61)Вычисление площади в полярных координатах.

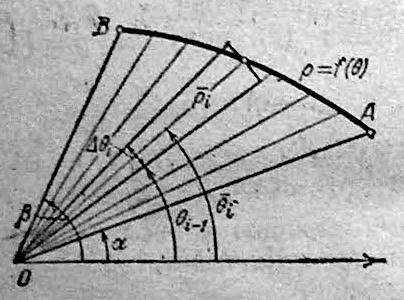
62)Вычисление длины дуги плоской кривой.

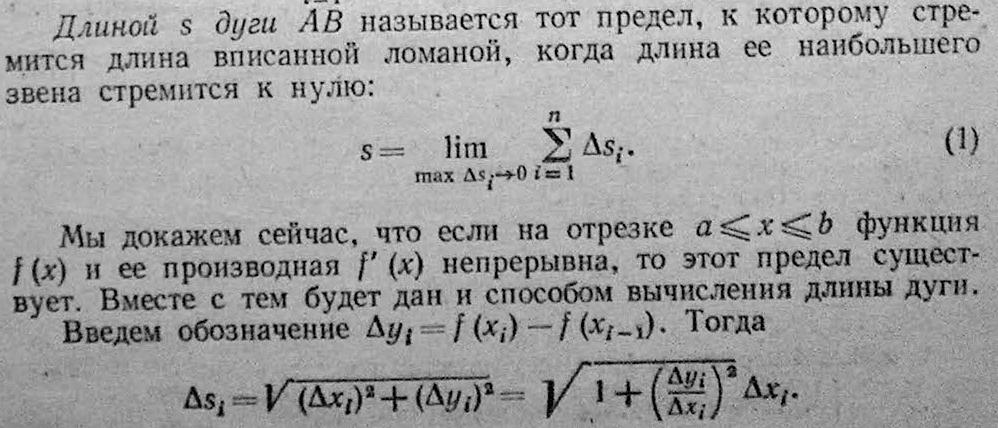
63)Вычисление длины дуги, заданной в параметрической форме.

Вычисление длины дуги в полярных координатах.

64)Нахождение координат центра тяжести плоской фигуры единичной толщины.

65)Вычисление объемов тел по площадям поперечных сечений.

Пусть имеем тело Т. Предположим, что известно любое сечение данного тела, плоскостью перпендикулярной оси ОХ. Эта плоскость будет зависеть от положения секущей плоскости и будет яв-ся ф-ей от х Q=Q(x). Проведем плоскости x=x0=a x=x1, x=x2,….,x=xn=b. Эти плоскости разобьют тело на слои. В каждом промежутке выберем такую, что x <= <=x и для i=1…n, построим тело образующая которого параллельна оси ОХ, теперь найдем объем данного тела, равный сумме слоев, каждый из которых равен

Q( ) x , тогда объем всего тела:

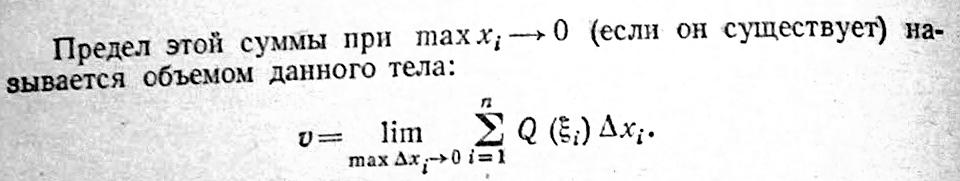
Так как представляет собой интегральную сумму для непрерывной ф-ции Q(x) на [a,b].

То указанный предел вычисляется: V=

Вычисление объемов тел вращения.

если вращение тела вокруг оси Ох, то сечением яв-ся круг, то объем по формуле будет равен:

если тело вращается вокруг оси ОУ, тогда секущей плоскость будет замкнута, тогда ее площадь можно вычислить по фор-ле произведения длины окружности на высоту(т.е. на значение самой ф-ции) => S=2 R f(x)=2 x f(x), тогда V=