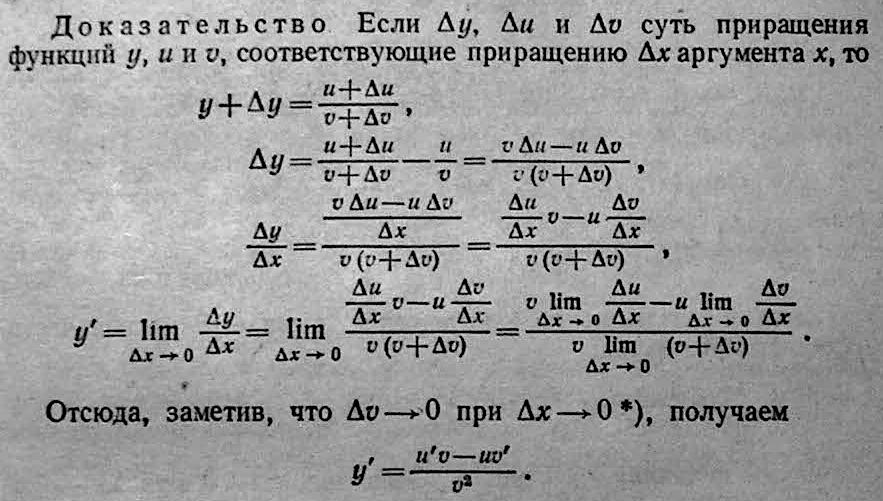29)Производные высших порядков для ф-ций, заданных параметрически и неявным образом.

Пусть обе ф-ции имеют производную на этом промежутке и для непрерывной ф-ции сущ обратная.

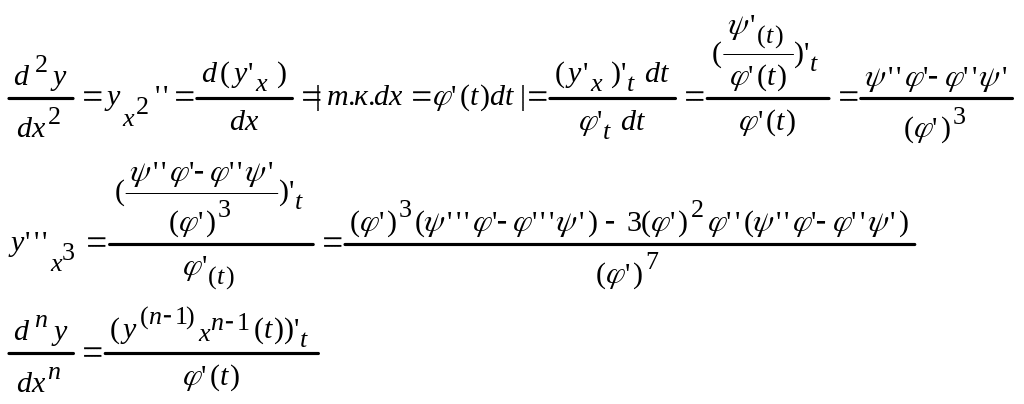Производные высших порядков для ф-ции заданной неявно.

Пусть y=f(x) задана неявным образом F(x,y(x))=0

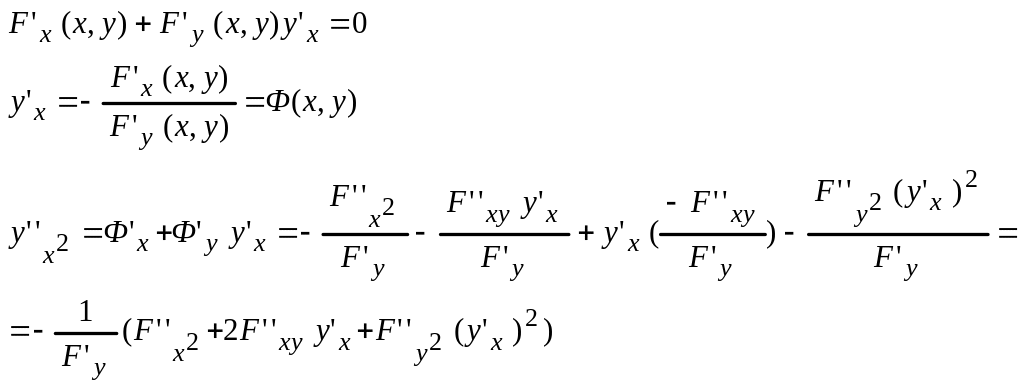
10) Замечательные пределы.

Первый при x0 sinx/x=1

Второй замечательный предел

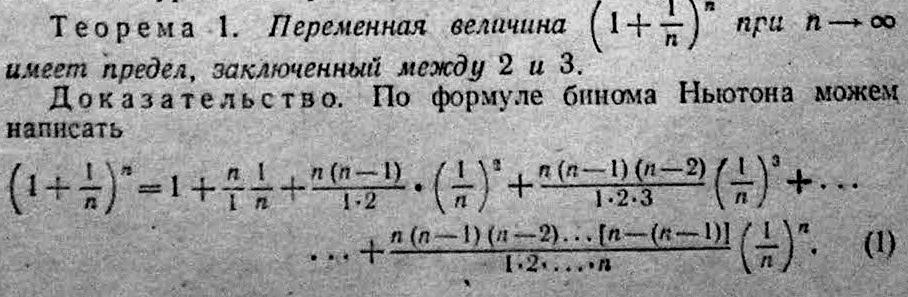
Замечание: под x можно понимать все что угодно.

35)Условия монотонности ф-ции.

Рассмотрим функцию монотонно возрастающую в широком смысле.

Теорема1: пусть функция определена и непрерывна на промежутке x[a,b], и внутри этого промежутка имеет конечную производную. для того чтобы функция монотонно возрастала необходимо и достаточно чтобы f ‘(x)0, для всякого x[a,b],( чтобы убывала

f ‘(x)0, на отрезке x[a,b])

Док – во: если функция монотонно возрастает то для всякого x[a,b] и x0, будем иметь f(x+ x) f(x), тогда , следовательно

Пусть f ‘(x) 0, x1<x2, x1,x2[a,b], по теореме Лагранжа в указанном промежутке существует точка С f(x2)-f(x1)= f ‘(c)(x2-x1) 0. следовательно f(x2) f(x1).

Теорема 1* пусть функция определена и непрерывна на промежутке x[a,b], имеются производные. Для того чтобы функция монотонно возрастала в строгом смысле необходимо и достаточно 1) f ‘(x)0 (а,б); 2) f ‘(x)0 не в каком промежутке составляющая часть (а,б).

Замечание: для практических целей пользуются достаточностью целого f ‘(x)>0 всюду за исключением конечного числа значения.

17)Производная ф-ции одной действительной переменной

Определение производной

24)Логарифмическая производная.

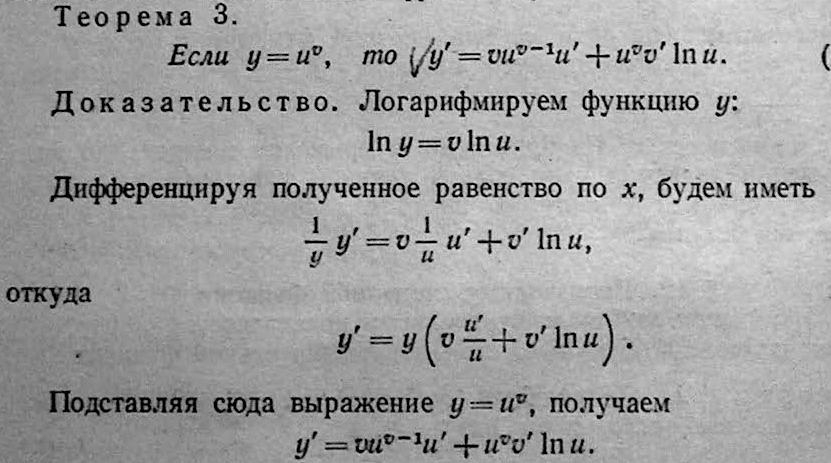
26)Основные формулы и правила д-ия.

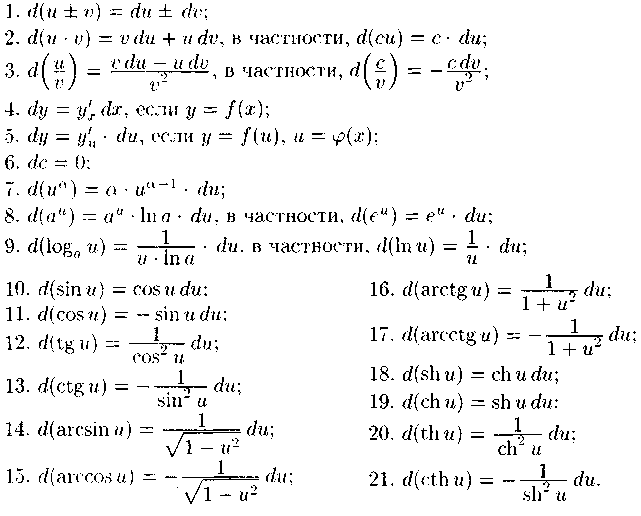Учитывая формулу dy=f ’(x)dx, и праила нахождения производных=>

19)Формула для приращения ф-ции. Непрерывность ф-ции имеющей производную.

Пусть f(x) [a,b] Возьмем x₀(a,b) и x₀ +x (a,b) Тогда данному приращению y=f(x₀ +x)-f(x). Покажем следующее 1) если f(x) в точке x₀ имеем конечную производную , то приращение этой функции может быть представлена следующим образом:

f(x₀)= f ‘ (x₀) x+ x, где  бесконечно малая x0. и 0 формула для преращения функции.

Доказательство:

По определению производной имеем при x0 lim f (x0)/ x, отсюда f (x0)/ x=f ’(x) следовательно f (x0)/ x=f ’(x) + отсюда f (x0)/ x=f ’(x) +x

2) если f(x) в точке x₀ имеет конечную производную в точке_, функция непрерывна. Если y= конечной производной то справедливо f(x₀)= f ‘ (x₀) x+ x

Доказательство: в силу конечности производной , следовательно

y=f (x) непрерывна.

20)Простейшие правила вычисления производных.

Теорема: производная постоянной равна нулю.

Док-во: y’=f(x)=c при любых х , дадим приращение x 0 => y+ y=f(x+ x)=c

=> y=f(x+ x)-f(x)=0 Найдем отношении предела: y/ x=0 => y’ =0.

Теорема: Пусть U=U(x) имеет производную в любой точки на заданном промежутке, когда U= C U(x) => y’ = C U’(x)

Док-во:

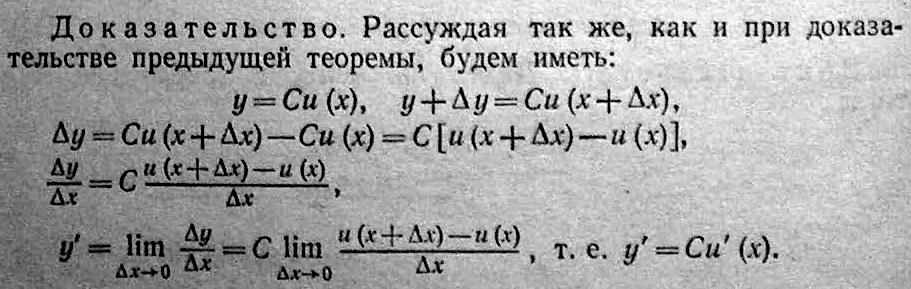
Теорема: Пусть ф-ция U(x) и V(x) имеют производную U’(x) и V’(x), тогда y=U(x) V(x)

имеет производную y’= U’(x) V’(x)

Док-во: для аргумента х y= U(x)+ V(x), для аргумента x+x y+ y=U(x+ x)+V(x+ x),

где y, x, U, V – приращение ф-ции, следовательно: y= U+ V

тогда y/ x= U/ x+ V/ x => y’ =lim y/ x=

=lim U/ x+lim V/ x=U’(x)+V’(x)

Теорема: Пусть ф-ция V(x) и U(x) имеют производную U’ и V’ , тогда ф-ция y=U(x)/V(x) имеет производную y’ =( U’ V-UV’ )/ V^2