30)Поведение ф-ции на интервале (основные теоремы дифференцирования)

Лемма: Пусть функция имеет в точке x ₀ конечную производную, если производная больше нуля, то для значений x  x ₀ справа f(x)>f(x ₀), для x слева близкий к x ₀,

f(x)<f(x ₀),то если функция в точке x ₀ , имеет производную больше нуля, то функция в окрестности этой точки возрастает.

В случае односторонней производной в точке x ₀ , например справа данное утверждение сохраняется справа.

Док-во: по определения производной в точке x ₀ ,имеем следующее:

f ‘ (x ₀ )= , дано что производная 0. по определения предела найдется такая окрестность (x ₀ -; x ₀ +) в которой это отношение больше нуля.

В данной окрестности

, тогда возьмем x справа, т.е. x (x ₀ ; x ₀ +) , тогда x ₀ - >0, и следовательно f(x)-f(x0)>0, отсюда f(x)>f(x0).

Возьмем x ₀ слева , т.е. (x ₀ -; x ₀], f(x)-f(x0)<0, отсюда f(x)<f(x0).

Теорема Ферма:

3 1)Теорема Роля:

Замечание: Теорема работает при а и b неравное нулю, но равные м/д собой.

Замечание: Если ф-ция такова что производная сущ не везде, то теорема не справедлива, т.к в точке максимум может не иметь производную, например y=1-x^(2/3) в точке нуль, имеет максимальное значение, а производная y’=-2/ ( 3x^(1/3) ) не сущ.

32)Теорема Лагранжа:

Геометрический смысл

33)Теорема о приращении двух ф-ций(Коши)

Замечание: следует отметить, что нельзя доказать формулу Коши используя формулу Лагранжа для числителя и знаменателя. с1 не совпадает с точкой с2, и тем более с точкой с.

Геометрический смысл:

Тот же что и у теоремы Лагранжа, т.е. сущ точка на прямой, такая что касательная параллельна секущей АВ для случая, когда ф-ция задана параметрически.

36)Максимумы и минимумы. Необходимое и достаточное условие максимума и минимума. Общая схема нахождения экстремумы.

Максимум и минимум.

Пусть функция определена и непрерывна на закрытом промежутке, и не является монотонной, тогда найдутся такие части промежутка [, ] [a,b], в котором наибольшее и наименьшее значения достигаются.

Опр1 функция имеет в точке x0 Максимум и минимум , если эту точку x0 можно окружить такой окрестностью (x0-;x0+) содержащаяся в рассматриваемом отрезке [a,b] что для всякого x[, ] выполняется f(x)<f(x0), тогда максимум, f(x)>f(x0), тогда минимум.

Необходимое условие существования экстремума Пусть функция определена на закрытом промежутке, и имеет конечную производную на (а,б), тогда необходимое существование экстремума f ‘(x)=0, когда f ‘(x) существует для всякого x(a,b).

В точках которых f ‘(x) неопределенна или равна , также является подозрительной, стационарной, критической на экстремум. Указанное условие является лишь необходимостью но не достаточностью.

Достаточное условие существования экстремума если точка x0 является стационарной либо равна (подозрительна на экстремум), тогда

Пусть в некоторой окрестности точки x0 (x0-;x0+) f ‘(x0) существует , причем конечна слева и справа, если сохраняется определенный знак в окрестности x0 x (x0-; x0) и

x (x0; x0+), тогда 1) f ‘(x) <0 слева , справа >0, то в этом случае минимум

2) f ‘(x) >0 слева, справа <0, то в этом случае максимум.

3) если знак не меняется, то экстремума нет, возрастает >0, убывает <0.

Правило существование экстремума

Для исследования точки x0 подозрительную на экстремум , подставим в выражение для

f ‘(x) сначала слева x<x0 потом, справа значение x0, и посмотрим знаки ‘+’ на ‘-’ максимум, ‘-’ на ‘+’ минимум., смотрим равна нулю или бесконечности в точке, исследуем в окрестности точками, смотрим знак, экстремумы находим .

Замечание: основываясь на перемене знака производной нельзя заключить об наличии экстремума , н-р: 1/(x^2)

Правило достаточности экстремума

Для проверки критической точки x0 подставляем во f ‘’(x), f ‘’(x) >0 то минимум, f ‘’(x) <0 то максимум.

Замечание Данное правило имеет более узкий круг применения. Не используется если точка x0 не существует конечная производная , либо не существует f ‘’(x0), в случае f ‘’(x)=0. требуется более высокая производная.

Схема нахождения экстремумов:

1. ищем производную

2. находим критические точки: приравниваем производную нулю и находим действительные корни, находим значения, где производная терпит разрыв

3. исследуем знак производной слева и справа от точки.

4. вычисляем значения ф-ции в этой точке.

37)Нахождение наибольшего и наименьшего значения функции на отрезке.

40)Общая схема исследования ф-ции и построение графика.

38)Выпуклость и вогнутость кривой, точки перегиба.

39)Асимптоты кривых

41)Понятие первообразной ф-ции и неопределенный интеграл, основные св-ва и простейшие правила интегрирования.

Опр: ф-ция F(x) называется первообразной от ф-ции f(x) на отрезке [a,b], если во всех точках этого отрезка выполняется равенствоF’(x)=f(x) или dF(x)=f(x)dx.

Опр: нахождение для заданной ф-ции f(x) всех F(x) называется интегрированием.

Теорема: Если в некотором замкнутом или бесконечном промежутке Х ф-ция F(x) есть первообразная f(x) то и F(x)+C так же яв-ся первообразной для ф-ции f(x) на Х.

Док-во: По условию первообразной (F(x)+C)’=F’(x)=f(x).

если Ф’(x)=f(x), то F(x) и Ф’(x) отличаются на const С, т.е. Ф’(x)=F(x)+C.

Опр: Если F(x) явл-ся первообразной для f(x), то выражение F(x)+C называется неопределенным интегралом от ф-ции f(x) и обозначается . При этом f(x) называют подынтегральной ф-цией, f(x)dx подынтегральным выражением, знак знаком интеграла, С –производная const.

Замечание: Если ф-ция f(x) непрерывна на [a,b], то тогда для этой ф-ции существует первообразная, а значит неопределенный интеграл.

Замечание: Если пр-ную от любой элементарной ф-ции мы можем найти и которая будет выражаться ч/з элементарные ф-ции, то первообразную элементарной ф-ции не всегда можно найти.

Св-ва:

1. Производная от неопределенного интеграла равна подынтегральной ф-ции.

( f(x)dx)’=(F(x)+C)’=F’(x)=f(x).

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению.

d( f(x)dx)=f(x)dx

3. Нопределенный интеграл от дифференциала некоторой ф-ции равен этой ф-ции плюс производная постоянной.

dF(x)= F’(x)dx= f(x)dx=F(x)+C

43)Простейшие приемы интегрирования.

1. Неопределенный интеграл от конечного числа слагаемых равен суме интегралов от каждого из слагаемых.

(f1(x)+f2(x))dx= f1(x)dx+ f2(x)dx

Док-во: продифференцируем обе части равенства.

2.Постоянный множитель отличный от нуля можно выносить за знак интеграла

af(x)dx=a f(x)dx

3. f(ax)dx=1/aF(ax)+C

4. f(x+b)dx=F(x+b)+C

42)Таблица основных интегралов.

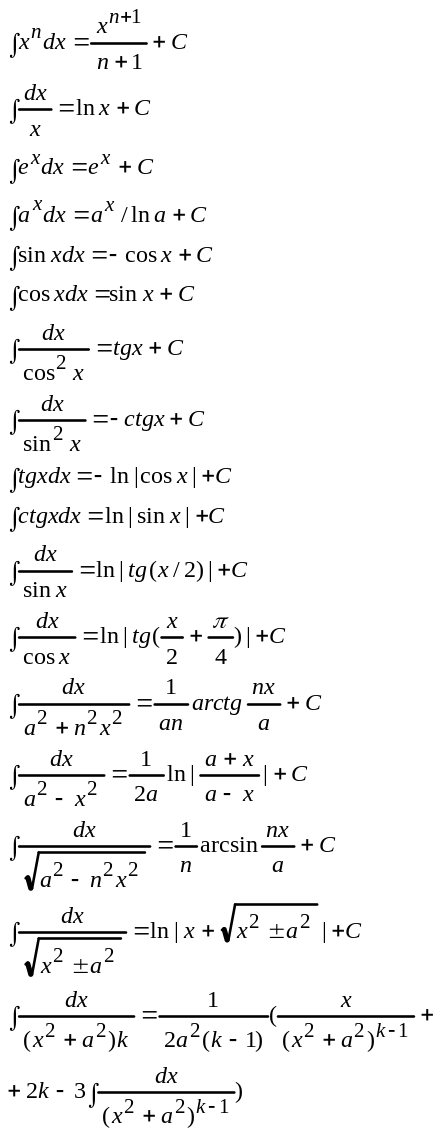
44)Интегрирование путем замены переменной.

Пусть требуется найти интеграл ф-ции f(x)dx, причем непосредственно найти первообразную мы не можем, тогда можно сделать замену подынтегрального выражения:

x= (t), тогда dx= ’(t)dt

Докажем, что: f(x)dx= f( (t)) ’(t)dt

Найдем производную левой части:

( f(x)dx)’=f(x)

Найдем производную правой части:

( f( (t)) ’(t)dt)’ =( f( (t)) ’(t)dt)’ dt/dx=f( (t)) ’(t))/ ’(t)=f( (t))=f(x)

Замечание: Иногда удобнее сделать замену t= тогда dt= ’(x)dx

Пусть нужно вычислить интеграл: ’(x)/ (x) dx= dt/t=ln|t|+C=ln| (x)|+C