13)Непрерывность суммы, произведения, частного и сложной ф-ции.

Аналогично для - * /

Теорема: Пусть ф-ция Z= определена в промежутке У, а ф-ция y=f(x) определена в промежутке Х, причем значения ф-ции у=f(x) не выходят за предел У, тогда если ф-ция y=f(x) непрерывна в точке Х0, а Z= непрерывна в точке у0, то сложная ф-ция Z будет не прерывна в точке x0.

Док-во: т.к. Z= непрерывна на у0

На основе данной теоремы можно утверждать, что суперпозиция ф-ций будет непрерывна, с помощью суперпозиций элементарных ф-ций получить класс непрерывных ф-ций.

Пр: Докажем что sinx для всех непрерывна

Ранне было замечено, что sinx<x 0<x<П/2, |sinx|<|x| для всякого х

|sinx-sinx0|=|2cos(x+x0)/2*sin(x-x0)/2|<=2|sin(x-x0)/2|<=x|(x-x0)/2|

9)Основные св-ва предельного перехода, а именно ограничение ф-ции имеющей предел, переход к пределу с равенством и неравенством. Предел монотонной ф-ции.

Теорема:

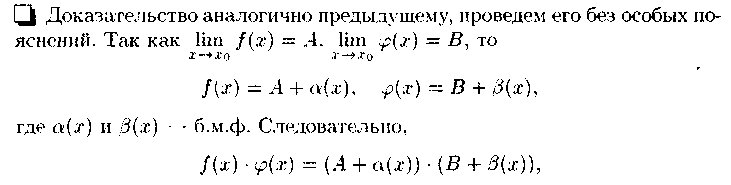
т.е. M’=|б|+E, то |f(x)|<M’, значит ф-ция ограничена.

Замечание: из определения следует, что при xa или xoo F(x)oо, т.е яв-ся ББ, то она яв-ся неограниченной, обратное утверждение не верно: неограниченная ф-ция может и не быть ББ. Пр: y=xsinx при xoo яв-ся не ограниченной, но обращается в нуль при x=0,П,2П

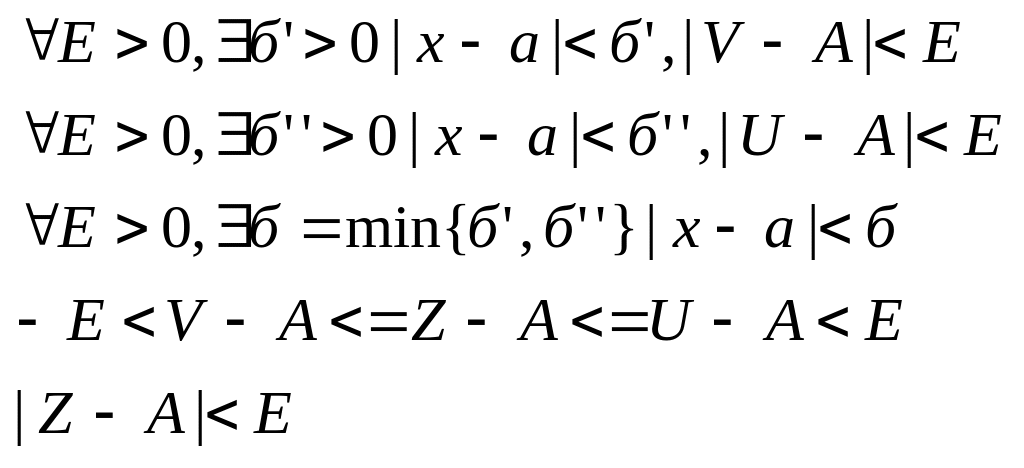
т.е при xa Z=AТеорема: если ф-ция v (переменная величина)монотонно возрастающая и ограничена сверху т.М, т.е v<M, то эта ф-ция (переменная величина) имееи предел lim v=a, где а<МВ противном случае предел равен +оо

Теорема: если ф-ция v (переменная величина)монотонно убывающая и ограничена снизу т.М, т.е M<v, то эта ф-ция (переменная величина) имееи предел lim v=a, где М<a.

В противном случае предел равен –оо. (док-во нет т.к. основывется на теории действительных чисел, дается в Фихтенгольдц)

16)Св-ва непрерывных ф-ций на отрезке.

Теорема: Об обращении ф-ции в ноль (Больцмана-Каши)

Пусть ф-ция f(x) определена и непрерывна в замкнутом промежутке [a,b] и на концах этого промежутка принимает значения разных знаков, тогда м/д точками а и b найдется хотя бы одна точка с в которой ф-ция обращается в ноль.

Теорема: о промежуточном значении или 2ая теорема Больцмана-Каши

Пусть y=f(x) определена и не прерывна в Х при этом Х может быть замкнутым или открытым, если в x=a, x=b, a<b, ф-ция принимает значения f(a)=A f(b)=B где А В, то каково бы ни было число С A<C<B всегда найдется точка x=c, такая что f(c)=С, что а<c<b

Теорема: 2-ая Вейерштрасса.

Если y=f(x) определена и непрерывна в замкнутом промежутке (a,b) то найдется такие точки х1 и х2 [a,b], то f(x1), f(x2) будут соответственно наибольшим и наименьшим значением ф-ции f(x) на указанном промежутке. При этом данная функция принимает все значения между наим. и наиб. значением.

27)Инвариантность формы дифференциала.

Применение дифференциала к приближенным вычислениям.

Применение дифференциала к приближенному вычислению значений ф-ции основано на замене приращения которое зависит от , т.е как уже говорилось а от отличаются значением БМ величиной наивысшего порядка, особенно от равенство верно при , т.е.