66) Приложение определенного интеграла для решения ф-их задач.
S=vt S=
A=FS A=
M=S
M=
67)Несобственные интегралы.
Интегралы с бесконечными пределами первого рода.
Опр: Пусть ф-ция f(x) определена и непрерывна для всех х, таких что a<=x<=+oo. Тогда рассмотрим интеграл от а до b ф-ции f(x), этот интеграл имеет смысл когда b>a, при изменении b интеграл меняется, он яв-ся непрерывной ф-цие b. Если же подынтегральное выражение неопределенно или же неограниченна, т.е. отрезок не конечный, то в этом случае имеем несобственный интеграл.
Опр: Пусть f(x) всюду непрерывна на промежутке [a,oo], тогда если существует конечный предел интеграла от a до boo, то этот предел называют несобственным интегралом первого рода от ф-ции на интервале [a,oo] и обозначается:
Опр: Если указанный предел существует и равен конечному числу, то говорят что несобственный интеграл сходится.
Если же не существует или не имеет конечного значения, то говорят что несобственный интеграл расходится.
Геометрический смысл: ограничен осью ОХ, прямой х=а, f(x), выражает площадь бесконечной облати.
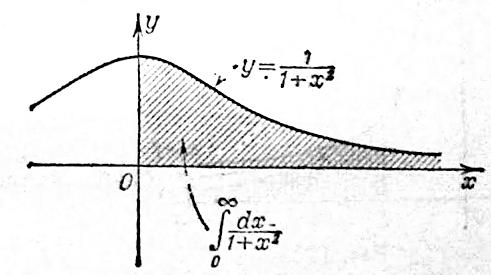
68)Признаки сходимости несобственного интеграла.
Во многих случаях бывает достаточным установить сходится или расходится данный интеграл, и оценить его значение. Для этого могут быть полезны следующие теоремы.
Теорема: Пусть для любых х >=a выполняется нер-во: f(x)>=0 и f(x)<= (x)
1. Если
(x)dx
сходится то и
f(x)dx
сходится
2. Если f(x)dx расходится то и (x)dx расходится
Теорема: если f(x)dx сходится то:
f(x)dx называется абсолютно сходящимся если сходится |f(x)|dx
f(x)dx называют условно сходящимся, если |f(x)|dx расходится
Замечание: если |f(x)|dx сходится то всегда и f(x)dx (обратное неверно)
Теорема: Если
существует конечный предел
при
xoo,
f(x)>0,
g(x)>0,
для все х
[a,oo],
то интегралы от f(x)
и g(x)
вместе сходятся и расходятся.
69)Несобственные интегралы второго рода.
В случае, когда подынтегральная ф-ция не ограничена.
Опр: Пусть
ф-ция f(x)
определена и непрерывна на [a,b]
и при x=b
f(x)
либо не определена, либо имеет разрыв,
тогда конечный предел при E0
если
он существует, называются несобственным
интегралом второго рода.
Опр: если предел существует и конечен, то говорят, что несобственный интеграл сходится, иначе, если не существует или равен бесконечности, то говорят, что несобственный интеграл расходится.
70)Признаки
сходимости несобственных интегралов
второго рода.
Если подынтегральная функция меняет знак на отрезке интегрирования, то применяем следующий признак сравнения для исследования сходимости.
Теорема 4 если
x[a,b),
имеем неравенство |f(x)|(x),
x=b,
либо не определен, либо имеет разрыв,
тогда если сходиться
то сходиться
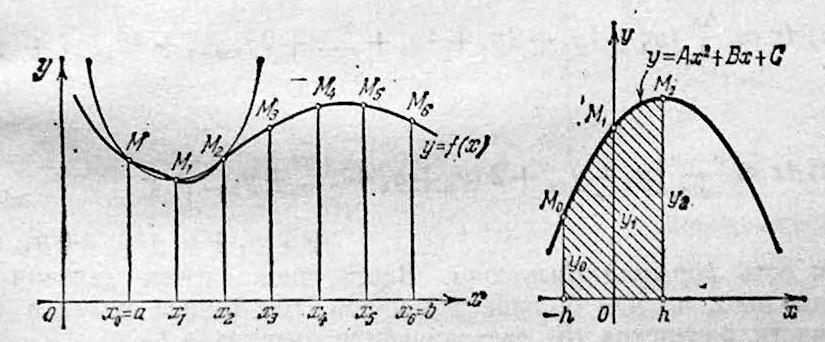
71)Метод прямоугольников.
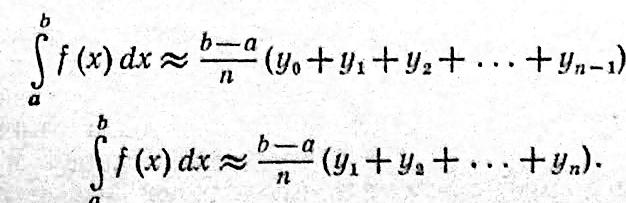
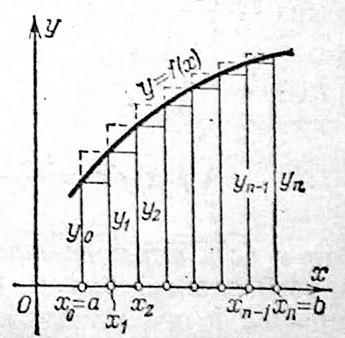
Метод трапеций.
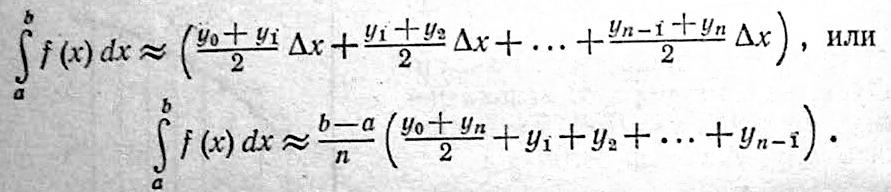
72)Метод парабол Симпсона.
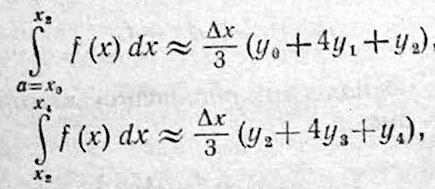
64)Нахождение координат центра тяжести плоской фигуры единичной толщины.
63)Вычисление длины дуги, заданной в параметрической форме.
55)Основные св-ва определенного интеграла.
1. Постоянный множитель можно выносить или нет за знак определенного интеграла.
(если f(x) интегрируема, то и Af(x) интегрируема), то выполняется
Док-во:
2. Определенный интеграл от алгебраической суммы нескольких ф-ций равен алгебраической сумме интегралов от слагаемых.
Док-во:
3. Если на отрезке [a,b] при a<b ф-ции f(x) и (х) удовлетворяют условию: f(x) < (х),то
Док-во:
4. Если m и M наименьшее и наибольшее значение ф-ции f(x) на отрезке [a,b] и a<b,то
Док-во: