
- •2. Объектами гидромеханики являются капельные и упругие (газы) жидкости.
- •Глава I. Основы гидростатики
- •Глава 2. Основы гидродинамики
- •2.1. Основные уравнения кинематики и динамики невязкой жидкости
- •Уравнение неразрывности (сплошности, постоянства расхода)
- •3.2. Дифференциальные уравнения движения жидкости
- •Дифференциальные уравнения движения Навье-Стокса
- •Теорема жуковского о подъемной силе и направлении движения вихрей
- •Принцип подобия, как основа физического моделирования однофазных систем.
- •Закон сопротивления при движении однофазного потока
- •Основы теории гидравлических сопротивлений
- •2. Основное уравнение равномерного движения
- •3. Основной закон вязкого сопротивления
- •4. Касательное напряжение
- •5. Закон распределения скоростей при турбулентном движении.
- •Способы определения потерь напора при равномерном турбулентном движении
- •Местные сопротивления.
- •Лекция № 12 Истечение жидкости из отверстий
- •1. Истечение в атмосферу при постоянном напоре через малые отверстия в тонкой стенке
- •2. Истечение через большие отверстия в атмосферу.
- •3. Истечение через затопленное большое отверстие.
- •4. Истечение через насадки
- •8.1. Общие понятия
- •8.2. Основная формула расхода водослива
- •8.3. Водослив с острым порогом
- •8.3.1. Формы струй
- •8.3.2. Основные задачи гидравлического расчета
- •8.3.3 Определение коэффициента расхода
- •8.5. Водослив практического профиля
- •Лекция №14 Элементы реологии Течение неньютоновских жидкостей
- •Гидродинамика кипящих (псевдоожиженных) зернистых слоев
- •Механизм переноса вещества и законы диффузии
- •1. Основные понятия и определения
- •Критерии подобия процессов массопередачи в однофазном потоке
- •Основы теории турбулентного массопереноса в процессах обогащения (сепарации).
- •Уравнение (1.24) принимает вид
- •Давление частиц рв на эту пластинку сверху равно
- •Соответственно извлечение частиц этого сорта составит:
- •Гидроциклоны – аппараты, использующие вихревые турбулентные потоки для разделения минералов по плотности и классификации их по крупности.
Дифференциальные уравнения движения Навье-Стокса
При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.
Действие
сил трения Т
на выделенный
в
потеке
вязкой жидкости элементарный
параллелепипед (рис.1) проявляется в
возникновении на его поверхности
касательных напряжений τ.
Рассмотрим первоначально относительно
простой случай одномерного плоского
потока капельной жидкости в направлении
оси х,
когда
проекция скорости
![]() зависит только от расстояния z
до
горизонтальной плоскости отсчета.
зависит только от расстояния z
до
горизонтальной плоскости отсчета.
 этих условиях касательные напряжения
возникают лишь ни поверхностях dF
верхней и
нижней граней элементарного параллелепипеда,
причем dF=
dxdy.
этих условиях касательные напряжения
возникают лишь ни поверхностях dF
верхней и
нижней граней элементарного параллелепипеда,
причем dF=
dxdy.
Рис.1. К выводу уравнений Навье-Стокса.
Если
касательное напряжение на нижней грани
параллелепипеда равно τ, то на верхней
оно составляет
![]()
При
этом направления касательных напряжений
на нижней и верхней гранях обусловлены,
например, тем, что более медленные
вышележащие слои жидкости затормаживают
слой, в котором находится параллелепипед,
а более быстрые нижележащие слои
«разгоняют» его. Производная
![]() выражает изменение касательного
напряжение вдоль оси z
в
точках, лежащих на нижней грани
параллелепипеда,a
выражает изменение касательного
напряжение вдоль оси z
в
точках, лежащих на нижней грани
параллелепипеда,a
![]() представляет
собой изменение этого напряжения вдоль
всей длины dz
ребра
параллелепипеда.
представляет
собой изменение этого напряжения вдоль
всей длины dz
ребра
параллелепипеда.
Тогда проекция равнодействующей сил трения на ось х
![]() (8)
(8)
Подставив
в это выражение значение касательного
напряжения τ
по уравнению Ньютона:
![]() ,
где
μ
— вязкость жидкости, получим
,
где
μ
— вязкость жидкости, получим
 (9)
(9)
В более общем случае трехмерного потока составляющая скорости будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось х примет вид
 (10)
(10)
Сумму вторых производит по осям координат называют оператором Лапласа:
![]() (11)
(11)
Следовательно, проекция равнодействующей сил трения на ось x может быть представлена как
![]()
Соответственно проекции равнодействующей сил трения на ось y:
![]()
на ось
z
![]()
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:
на ось х
![]()
на ось y
![]()
на ось z
![]()
Суммы
проекций сил на оси координат, в
соответствии с основным принципом
динамики, должны быть равны произведению
массы жидкости![]() (
(![]() -плотность
жидкости), заключенной в элементарном
объеме, на проекции ускорения на оси
координат. Поэтому, приравнивая проекции
равнодействующей произведениям массы
на проекции ускорения, после сокращения
на dxdydz,
получим
-плотность
жидкости), заключенной в элементарном
объеме, на проекции ускорения на оси
координат. Поэтому, приравнивая проекции
равнодействующей произведениям массы
на проекции ускорения, после сокращения
на dxdydz,
получим

![]()
![]() (12)
(12)
![]()
где соответствующие субстанциональные производные выражены для установившегося и неустановившееся потоков уравнениями (12)
Уравнения (12) представляют собой уравнения Навье-Стокса, описывающие движение вязкой капельной жидкости.
Дифференциальные уравнения вихревого движения жидкости (Громеки)
Разделим правую и левую части уравнения Эйлера на плотность жидкости ρ:
![]()
![]() (13)
(13)
![]()
Полная скорость частицы, через осевые составляющие определяется по уравнению:
![]() (2)
(2)
Частные производные от обоих частей уравнения (2) по xyz будут:
![]()
![]() (3)
(3)
![]()
Вычитая из обеих частей уравнения Эйлера (1) равенства (3 – поступательное движение) после перегруппировки с выделением элементов вращения, получим

 (4)
(4)

Обозначая
![]() ,
,![]() ,
,![]()
получим
![]()
![]()
![]()
Иногда эти уравнения называют уравнениями Эйлера в форме Громеки.
Математические модели движения жидкости в векторной форме.
Уравнение Эйлера
![]()
идеальная
жидкость (![]() ).
).
Уравнение
Навье-Стокса
![]()
реальная
жидкость (![]() ).
).
Уравнение Громеки
![]()
вихревое движение жидкости
Лекция 5.
Общие сведения о вихревом движении.
Вихревой скоростью называется мгновенная угловая скорость бесконечно малой жидкой частицы.
Вихревой линией называется линия, в каждой точке которой в данный момент вектор вихревой скорости жидкости к ней касателен (см. рис. 1.).
Дифференциальное уравнение вихревых линий имеет вид:
![]() (1)
(1)
 или в виде
двух совокупных уравнений:
или в виде
двух совокупных уравнений:
![]() ;
;
![]() ;
(2)
;
(2)
Вихревой трубкой (вихревым шнуром, вихревой нитью) называется часть жидкости, ограниченная вихревыми линиями, проведенными через все точки какого-нибудь бесконечно малого замкнутого контура, находящегося в области, Рис. 1. Вихревая линия (а) и занятой жидкостью. вихревая трубка (б).
Вихревая трубка представляет собой циркуляционный поток жидкости бесконечного малого сечения df.
Вихревой поверхностью называется поверхность, ограничивающая вихревую трубку.
Интенсивностью или напряжением вихревых трубок называется удвоенное произведение угловой скорости на площадь поперечного сечения трубки:
![]() [м2/сек].
(3)
[м2/сек].
(3)
Важнейшим свойством вихревой трубки является постоянство напряжения по длине трубки, т. е. аналогично постоянству расхода имеем:
![]() (4) или
(4) или
![]() (5)
(5)
Согласно уравнению (II, 60) в меньшем сечении трубки возникает большая угловая скорость. Вследствие этого вихревая трубка не может оканчиваться в жидкости, так как при уменьшении сечения трубки до нуля угловая скорость стала бы бесконечно большой.
Вихревые трубки внутри ограниченного объема жидкости заканчиваются или на стенках сосуда, или на свободной поверхности жидкости, или же образуют замкнутые вихревые кольца.
Интенсивность вихревой трубки может оцениваться также циркуляцией скорости. Это аналогично понятию работы сил в теоретической механике.

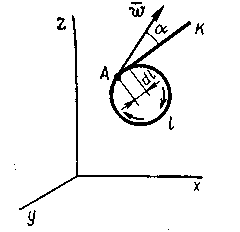
![]() в точке A,
а касательная к контуру К.
Угол,
образованный между вектором скорости
и
в точке A,
а касательная к контуру К.
Угол,
образованный между вектором скорости
и
Рис. 2. К понятию о циркуляции Рис. 3. Циркуляция вектора
вектора скорости по замкнутому контуру.
касательной К, обозначим через а. Если взять сумму произведений проекций скорости на соответствующую касательную в каждой точке контура на элемент длины линии контура dl, то получим так называемую циркуляцию по контуру:
![]() [м2/сек] (6)
[м2/сек] (6)
Если обозначить углы между направлением касательной и осями координат через α1, β1, γ2 а углы между направлением скорости и осями координат — через α2, β2, γ2 то между этими углами и углом а будет существовать следующая зависимость:
![]()
Выразим косинусы через скорость и элементы дуги и их проекции на оси координат:
![]() (7)
(7)
Подставляя (II, 62) в уравнение циркуляции, получим
![]() [м2/сек]
(8)
[м2/сек]
(8)
Уравнение (II, 63) аналогично уравнению суммы элементарных работ в механике, только здесь роль силы играет скорость. Исходя из выражения (II, 63), циркуляцию скорости Г можно определить как работу скорости на замкнутом контуре:
![]() [м2/сек]
(9)
[м2/сек]
(9)
Для установления связи между циркуляцией и интенсивностью вихревой трубки выделим внутри жидкости бесконечно малый замкнутый контур abсd со сторонами dy и dz (рис. 66).
Допустим,
что в точке а
(х, у, z)
этого
контура скорости wx,
wy,
wz.
На
сторонах
![]() и
cd
действуют
скорости соответственно wy
и
и
cd
действуют
скорости соответственно wy
и
![]() ,
а их сумма
,
а их сумма ![]() ;
на
сторонах bc
и
da
действуют
скорости соответственно wz
и
;
на
сторонах bc
и
da
действуют
скорости соответственно wz
и
![]() ,
а
их сумма
,
а
их сумма
![]() .
Составляя выражение для циркуляции по
всему бесконечно
малому контуру abсd,
согласно
уравнению (11,63), надо просуммировать
произведения скорости на длины отдельных
сторон:
.
Составляя выражение для циркуляции по
всему бесконечно
малому контуру abсd,
согласно
уравнению (11,63), надо просуммировать
произведения скорости на длины отдельных
сторон:
![]() (I0)
(I0)
Согласно уравнению Громеки:
![]()
Поэтому
![]()
но по уравнению (11,58)
![]() ,
,
и, следовательно,
![]() .
(12)
.
(12)
Таким образом, циркуляция по контуру равна напряжению вихревой трубки, проходящей через этот контур.
Равенство (II, 67) следует и из соображений размерности. Действительно, в выражение интенсивности вихревой трубки входит угловая скорость и площадь сечения, в то время как в уравнение циркуляции входит окружная скорость и длина — в результате в обоих случаях получаем одну и ту же размерность (м2/сек).
Аналогичное соотношение между интенсивностью и циркуляцией получаем для контура любых конечных размеров, что формулируется в виде теоремы Стокса: скорость циркуляции по замкнутому контуру равна сумме напряжений всех вихревых трубок, проходящих через этот контур.
В соответствии с постоянством напряжения по длине трубки для замкнутого контура производная циркуляции по времени равна нулю:
![]() (13)
(13)
т. е. циркуляция по контуру не зависит от времени (теорема В. Томсона). С течением времени может меняться скорость и площадь сечения вихревой трубки, но произведение их остается постоянным, т. е. напряжение вихревой трубки во время движения остается постоянным. Для идеальной жидкости формулируется принцип сохранения вихрей: в идеальной жидкости жидкая масса, образующая вихревую трубку, движется, оставаясь все время вихревой трубкой, напряжение которой постоянно по всей длине, и не изменяется с течением времени. Согласно принципу сохранения вихрей, если вихрь существует, то он сохраняется вечно. Однако этот вывод относится только к идеальной жидкости. В вязкой реальной жидкости вихри возникают и затухают под влиянием вязкости.


Рис. 4. К определению скорости, Рис. 5. Схема взаимодействия
порождаемой вихрем. двух вихрей.
В реальных жидкостях принцип сохранения вихрей переходит в принцип устойчивости форм вихревого движения. Во всех практических случаях вихри обладают значительной устойчивостью.
Наличие
в жидкости вихрей вызывает появление
в ней добавочных скоростей, что
увеличивает перенос субстанции и
существенно влияет на природу процессов
массообмена. Обозначим скорость жидкости
в любой точке С
(рис.
4), вызываемую действием элементарного
отрезка вихря dl,
через
![]() и
расстояние этой точки С от вихря — через
А;
угол,
составленный прямой ОС и осью вращения
z-z,
через θ. Если интенсивность вихревой
трубки равна J
и
скорость циркуляции — Г, то вычисление
скоростей движения, порождаемого
вихрями, в общем случае производится
по уравнению
и
расстояние этой точки С от вихря — через
А;
угол,
составленный прямой ОС и осью вращения
z-z,
через θ. Если интенсивность вихревой
трубки равна J
и
скорость циркуляции — Г, то вычисление
скоростей движения, порождаемого
вихрями, в общем случае производится
по уравнению
![]() .
(14)
.
(14)
Если имеется несколько вихрей, то, взаимодействуя между собой, они создают перемещение вихревых систем в пространстве.
Если
в точке С (см. рис. 4) будет находиться
второй вихрь с противоположно направленной
циркуляцией Г2,
то схему взаимодействия двух вихрей
можно представить рис. 5. Приняв длину
элементарных отрезков вихрей
![]() и расстояние между двумя вихрями А=а
при
θ= 90°, на основании уравнения (II,
68) получим, что один вихрь будет возбуждать
перемещение второго со скоростью
и расстояние между двумя вихрями А=а
при
θ= 90°, на основании уравнения (II,
68) получим, что один вихрь будет возбуждать
перемещение второго со скоростью
![]() , (11,
70)
, (11,
70)
в то время как второй будет возбуждать перемещение первого со скоростью
![]() , (11,
71)
, (11,
71)
При этом положительной циркуляции Г1 отвечает движение по окружности по часовой стрелке.


Рис. 6. Поле скоростей, создаваемое Рис, 7. Поле скоростей, создаваемое вихрем двумя вихрями
В области вихревой трубки вся масса жидкости будет получать от вихря скорость (рис. 6), которая будет максимальной на поверхности вихревой трубки r0 , а затем по мере увеличения расстояния от оси скорости постепенно уменьшаются. Если будем иметь вихревую пару, то распределение скорости в поле действия этой пары будет таким, как показано на рис. 70. Под влиянием скорости движения, возбуждаемого вихрем,
![]()
вихревая пара будет перемещаться поступательно в пространстве по прямолинейному направлению перпендикулярно к кратчайшей прямой а, соединяющей оба вихря. При различном направлении вихрей они будут перемещаться относительно общего центра наподобие планет. Если же вихревая пара имеет циркуляцию по одному направлению, то центр вращения пары лежит на середине расстояния.
Д ля
процессов массообмена, осуществляемых
в промышленных аппаратах, часто
характерным является обтекание потоком
различных элементов аппарата. Поэтому
представляет практический интерес
движение образуемых вихрей за обтекаемым
телом.
ля
процессов массообмена, осуществляемых
в промышленных аппаратах, часто
характерным является обтекание потоком
различных элементов аппарата. Поэтому
представляет практический интерес
движение образуемых вихрей за обтекаемым
телом.
При некоторой скорости, зависящей от вязкости и ширины обтекаемого тела, позади него начинают отрываться вихри поочередно справа и слева. На некотором расстоянии за телом устанавливаются определенные расстояния между вихрями, причем вихри в зависимости от формы обтекаемого тела располагаются как симметрично, так и в шахматном порядке (рис. 71); вихри обоих рядов имеют противоположное вращение, т. е. Г1 =
Рис. 71 Г2. Расстояние h между рядами вихрей (ширина вихревого слоя) не зависит от скорости, а зависит от ширины тела. Один ряд вихрей называется вихревой цепочкой.
Скорость перемещения вихревых цепочек:
при симметричном расположении
![]()
![]() , (11,
72 )
, (11,
72 )
при шахматном расположении
![]() (11,
73)
(11,
73)
Условием устойчивости вихревых цепочек является равенство [4]
![]() (11,
74)
(11,
74)
Так как вихри вызывают появление в жидкости добавочных скоростей, то эти скорости, в свою очередь, сообщают жидкой массе количество движения, определяемое уравнением Жуковского:
![]() ,
(11, 75)
,
(11, 75)
Где М – количество
движения, равное
![]() кГ/сек; m-
масса жидкости,
кГ/сек; m-
масса жидкости,
![]() ;
v
– скорость жидкости, м/сек; ρ – плотность
жидкости,
4;
Г- циркуляция, м2/сек;
а – расстояние между двумя соседними
вихрями каждой цепочки, м; h
– ширина вихревых слоев, м.
;
v
– скорость жидкости, м/сек; ρ – плотность
жидкости,
4;
Г- циркуляция, м2/сек;
а – расстояние между двумя соседними
вихрями каждой цепочки, м; h
– ширина вихревых слоев, м.
Уравнение (II, 75) представляет собой математическое выражение теоремы Н. Е. Жуковского; количество движения, сообщаемое безграничной массе жидкости двумя параллельными между собой, прямолинейными и непрерывными вихревыми слоями конечной ширины, одинакового напряжения и противоположного вращения, равно плотности жидкости, умноженной на циркуляцию вихрей, расстояние между слоями и на их ширину.
Это количество движения сообщается жидкости только в направлении по нормали к плоскостям слоев или параллельно направлению вихревых слоев или по продолжению.
Из этой теоремы следует, что один изолированный вихревой слой конечной ширины не сообщает жидкости никакого количества движения и не действует на жидкость как сила.
