3.5 Зразок виконання індивідуального семестрового завдання №5

Дискретна випадкова величина задана рядом розподілу. Знайти функцію розподілу і побудувати її графік. Знайти математичне сподівання, дисперсію випадкової величини та середнє квадратичне відхилення.

х	4	8	12
р	0,5	0,2	0,3

Розв’язання.

1) Математичне сподівання знайдемо за формулою

.

.

2) Дисперсію знайдемо за формулою

.

Складемо закон розподілу для :

	16	64	144
р	0,5	0,2	0,3

.

.

3) Середнє квадратичне відхилення знайдемо за формулою:

.

.

4) Знайдемо функцію розподілу:

5. Графік цієї функції має вигляд:

0,7

4

3.6 Неперервні випадкові величини

Якщо значення, які може приймати дана випадкова величина , заповнюють цілий кінцевий або нескінченний проміжок числової осі, то випадкова величина називається неперервною.

Неперервну випадкову величину неможливо задати за допомогою ряду або багатокутника розподілу, тому що множина її можливих значень нескінченна й незліченна.

Для характеристики поводження неперервної випадкової величини доцільно використати не ймовірність події , а ймовірність події , де — деяке дійсне число.

Якщо змінюється довільно, то ймовірність виконання нерівності в загальному випадку буде мінятися.

Отже, є функцією аргументу .

Функцією розподілу випадкової величини називається функція , що задає ймовірність того, що випадкова величина Х прийме значення, менше за , тобто

.

називають інтегральною функцією розподілу.

Неперервну випадкову величину можна задати також за допомогою функції, що називається щільністю розподілу.

Диференціальною функцією розподілу або щільністю розподілу ймовірностей називається перша похідна інтегральної функції розподілу, тобто .

Графік диференціальної функції розподілу називається кривою розподілу. Імовірність того, що в результаті випробування випадкова величина одержить значення, що належить інтервалові , можна знайти за формулою:

.

Геометрично ймовірність влучення випадкової величини в проміжок дорівнює площі відповідної криволінійної трапеції, обмеженої кривої розподілу, віссю 0х і прямими х = а, х = b.

Властивості щільності розподілу :

1) , для всіх ;

2) ;

3) ;

4) .

Якщо випадкова величина Х визначена в інтервалі , а — функція щільності розподілу ймовірності, то

Математичним сподіванням неперервної випадкової величини Х, можливі значення якої належать відрізку , називається визначений інтеграл

.

Дисперсією неперервної випадкової величини Х називається математичне сподівання квадрата її відхилення

.

Для обчислення дисперсії неперервної випадкової величини використають більше зручну формулу

.

Середнє квадратичне відхилення неперервної випадкової величини, як і для величини дискретної, визначається рівністю

.

Початковий теоретичний момент порядку неперервної випадкової величини визначається рівністю:

.

Центральний теоретичний момент порядку неперервної випадкової величини визначається рівністю:

.

Якщо всі можливі значення належать інтервалу , то

; .

Очевидно, що якщо

, то ;

, то .

Центральні моменти виражаються через початкові моменти формулами:

;

и т.д.

Модою неперервної випадкової величини називається таке її значення, при якому щільність ймовірності набуває максимуму.

Медіаною неперервної випадкової величини називається таке її значення, відносно якого рівноймовірно набування більшого або меншого значення випадкової величини, тобто

.

Центральний момент третього порядку характеризує асиметрію розподілу, тобто асиметрією називається відношення центрального моменту 3-го порядку до кубу середнього квадратичного відхилення:

.

Центральний момент четвертого порядку характеризує ексцес (крутість) розподілу і виражається рівністю

.

Приклад 1. Випадкову величину задано функцією розподілу:

Знайти: а) щільність розподілу ймовірності;

б) математичне сподівання;

в) дисперсію випадкової величини;

г) імовірність попадання випадкової величини в інтервал .

Розв’язання. а) щільність розподілу:

б) математичне сподівання:

.

в) дисперсія:

.

г) імовірність попадання випадкової величини в інтервал :

.

Приклад 2. Дана .

Знайти: , та побудувати ії графік.

Розв’язання.

Враховуючи вигляд і властивості , дістанемо:

Отже:

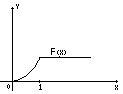
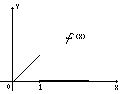
Приклад 3. Випадкову величину х задано щільністю розподілу в інтервалі ; за інтервалом . Знайти: а) моду; б) медіану Х.

Розв’язання. а) Функція в відкритому проміжку не має максимуму, тому величина х моди не має.

б) Знайдемо медіану , виходячи з визначення медіани:

або .

Враховуючи, що , маємо:

або ,

звідси

,     .

Приклад 4. Випадкова величина х в інтервалі задана щільністю розподілу ; за інтервалом . Знайти моду, математичне сподівання та медіану величини х.

Розв’язування. Запишемо щільність розподілу у вигляді

.

Звідси видно, що при щільність розподілу досягає максимуму. Отже,

.

Крива розподілу симетрична відносно прямої , тому

.

Приклад 5. Випадкова величина х задана щільністю розподілу в інтервалі ; за інтервалом . Знайти початкові та центральні моменти першого, другого та третього порядків.

Розв’язування. За формулою

знайдемо початкові моменти :

;

;

.

Знайдемо центральні моменти:

;

;

.