2.2 Класичне означення ймовірності

Імовірність події — це чисельна міра об'єктивної можливості її появи.

Випадок називається сприятливим появі події, якщо поява цього випадку спричиняє появу події .

Ймовірністю події називається відношення числа випадків, що сприяють події , до загального числа всіх рівможливих несумісних результатів експерименту, що утворюють повну групу.

Нехай — загальне число можливих випадків, — число випадків, що сприяють події , тоді

.

Приклад 1. У групі 25 студентів. З них 12 юнаків й 13 дівчин. Випадковим образом до дошки викликають двох студентів. Яка ймовірність, що це дівчата?

Розв’язання.

.

Приклад 2. У партії з 8 деталей - 6 стандартних. Знайти ймовірність того, що з 4-х узятих навмання деталей 2 виявляться стандартними.

Розв’язання.

Загальне число п можливих результатів цього експерименту дорівнює числу способів, за якими можна взяти 4 деталі з наявних 8, тобто .

т – число результатів, яки сприяють події А (серед взятих 4 деталей є дві стандартні – , а інші дві повинні бути нестандартними – ).

Отже, , і шукана ймовірність

.

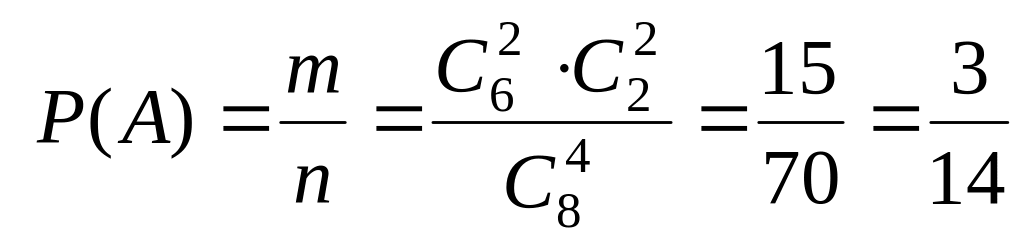2.3 Алгебра ймовірностей

Статистична ймовірність

Відносна частота появи події при досить великій кількості випробувань називається статистичною ймовірністю.

Геометрична ймовірність

Нехай на площині є деяка фігура , що містить фігуру . На фігуру навмання кидається точка, що може виявитися в будь-якій точці фігури . Нехай подія — влучення точці у фігуру , а й — площі фігур й відповідно.

Геометричною ймовірністю події називається відношення міри області, яка сприяє появі події, до мірі всієї області:

.

Аксіоми теорії ймовірностей

1. Кожній випадковій події відповідає певне число , що задовольняє подвійній нерівності

.

2. Ймовірність вірогідної події дорівнює 1: .

3. Ймовірність неможливої події дорівнює нулю: .

Теорема 1. Для будь-якої події ймовірність протилежної події виражається рівністю:

.

Теорема 2. Імовірність неможливої події дорівнює 0:

.

Теореми додавання ймовірностей

Теорема 1. Сума ймовірностей попарно несумісних подій , що утворюють повну групу, дорівнює 1.

Теорема 2. Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій

.

Теорема 3. Імовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без імовірності їхнього спільного настання, тобто

.

Наслідок. Сума ймовірностей протилежних подій дорівнює 1.

.

Умовна ймовірність. Теореми добутку ймовірностей

Означення 1. Події і називаються незалежними, якщо поява однієї з них при першому випробуванні не впливає на ймовірність появи іншої події при наступному випробуванні.

Приклад: підкидання двох монет («герб - решка»).

Означення 2. Події А і В називаються залежними, якщо поява однієї з них при першому випробуванні впливає на ймовірність появи іншої події при наступному випробуванні.

Приклад: у ящику 4 бракованих й 8 стандартних деталей, які дістають з ящика випадковим чином без повернення назад. Поява стандартної деталі при першому вийманні впливає на ймовірність появи стандартної деталі при другому вийманні, тобто ці дві події будуть залежні.

Означення 3. Якщо ймовірність події обчислюється за умови, що подія відбулася, то така ймовірність називається умовною й позначається

або .

Умовною ймовірністю події за умови, що настала подія , називається число

, .

Теорема 1. Імовірність сумісної появи двох залежних подій дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, за умови, що перша подія відбулася:

,

.

Теорема 2. Ймовірність добутку двох незалежних подій дорівнює добутку їхніх ймовірностей

.

Приклад 1. Три стрільця зробили по одному пострілу в ту ж саму мішень. Ймовірність влучення кожного з них відповідно дорівнює: 0,6; 0,7; 0,9. Знайти ймовірність того, що влучать у мішень 2 стрільці.

Розв’язання. Нехай події — влучення відповідно 1-го, 2-го й 3-го стрільця.

Тоді — подію, що влучать 2 стрільця, представимо в такий спосіб:

.

Тоді:

.

Приклад 2. Робітник обслуговує 3 верстати, які працюють незалежно друг від друга. Ймовірність того, що протягом години 1-й верстат потребує уваги працівника - 0,1, для іншого верстата - 0,2, для третього - 0,3. Знайти ймовірність того, що впродовж години хоча б один верстат потребуватиме уваги робітника.

Розв’язання. Нехай – подія, ймовірність якої треба знайти.

Тоді протилежна подія , яка полягає в тому, що жоден верстат не потребуватиме уваги робітника, може бути представлена таким чином:

.

Звідси випливає, що:

.

Приклад 3. Студент прийшов на екзамен, підготувавши лише 20 з 25 питань програми; екзаменатор задав йому три питання. Знайти ймовірність того, що студент знає відповіді на ці питання.

Розв’язання. Позначимо через подію “студент знає відповідь на питання, задане екзаменатором”, через подію “студент знає відповіді на всі три питання”. Тоді , і за формулою (4) маємо:

(оскільки питань залишилось 24, з них студент знає 19, бо перше питання студент знав).

Аналогічно

,

тоді

.

Приклад 4. Три стрільця зробили по одному пострілу по мішені. Ймовірність попадання для першого стрільця дорівнює 0,8, для другого – 0,7, для третього – 0,9. Знайти ймовірність того що:

1) влучив лише один стрілець;

2) влучили лише два стрільці;

3) влучили три стрільці;

4) влучив хоча б один стрілець.

Позначимо через подію “попав стрілець”.

1) Подія – попав лише один стрілець. Очевидно

.

Доданки в цій сумі – несумісні події, а в кожному доданку множини – незалежні події, тому ймовірність суми дорівнює сумі ймовірностей кожного доданку, а ймовірність добутків доданків дорівнює добутку ймовірностей множників. Одержимо:

2) Подія – влучили лише два стрільці:

.

3) Подія - влучили три стрільці: .

.

4) Подія - влучив хоча б один стрілець: ,

,

тоді