3.7 Тренувальні вправи

1. Випадкова величина в інтервалі задана щільністю розподілу за інтервалом . Знайти: моду, математичне сподівання та медіану випадкової величини .

.

2. Випадкова величина в інтервалі задана щільністю розподілу ; за інтервалом . Знайти дисперсію Х.

.

3. Знайти щільність розподілу, математичне сподівання та дисперсію величини Х, яка функцією розподілу:

.

4. Випадкова величина задана щільністю розподілу в інтервалі ; за інтервалом . Знайти початкові та центральні моменти першого, другого та третього порядків.

5. Задана інтегральна функція неперервної випадкової величини :

.

Знайти диференціальну функцію .

Відповідь: , поза проміжком .

6. Задана функція неперервної випадкової величини :

.

Знайти диференціальну функцію .

Відповідь: .

7. Задано диференціальну функцію неперервної випадкової величини : в інтервалі . Поза цим інтервалом . Знайти інтегральну функцію .

Відповідь: .

8. Задано диференціальну функцію неперервної випадкової величини :

Знайти інтегральну функцію .

Відповідь: .

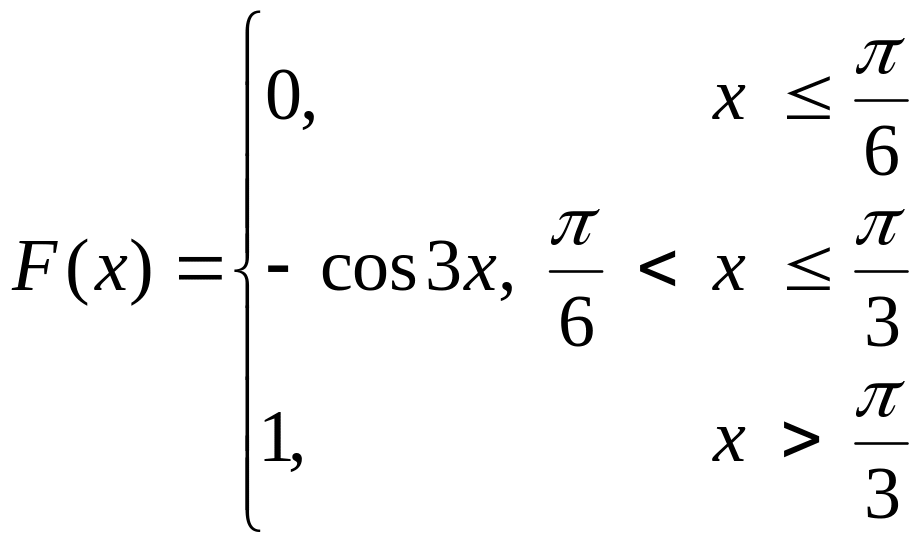3.8 Індивідуальне семестрове завдання №6

Випадкова величина задана функцією розподілу . Знайти:

а) щільність розподілу ймовірності;

б) математичне сподівання;

в) дисперсію випадкової величини;

г) імовірність попадання випадкової величини в інтервал ;

д) накреслити графіки функцій і .

1.

2.

3.

4.

5.

6.

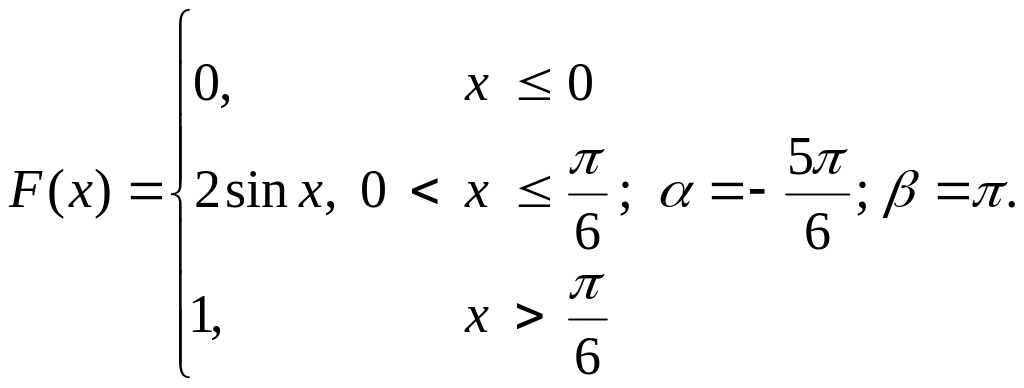
7.

8.

9.

10.

11.

12.

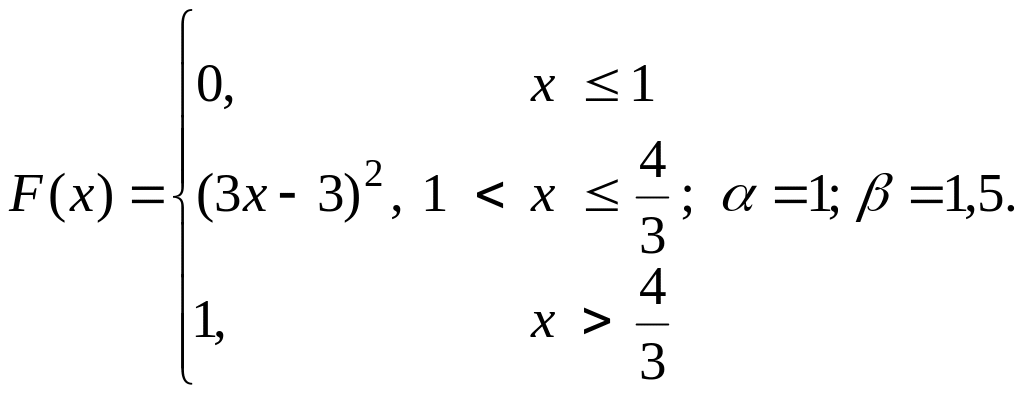
13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

3.9 Зразок виконання індивідуального семестрового завдання №6

Випадкова величина Х задана функцією розподілу:

Знайти:

а) щільність розподілу ймовірності;

б) математичне сподівання;

в) дисперсію випадкової величини;

г) імовірність того, що в результаті випробування випадкова величина прийме значення, що належить інтервалу .

Розв’язання.

а) щільність розподілу ймовірностей:

б) математичне сподівання

.

в) дисперсія

г) імовірність того, що випадкова величина прийме значення з інтервалу

.

3.10 Нормальний закон розподілу

Нормальним законом розподілу ймовірностей називається такий розподіл імовірностей неперервної випадкової величини, у якої щільність розподілу має вигляд

,

де — математичне сподівання;

— середнє квадратичне відхилення.

Функція задовольняє вимогам до щільності розподілу:

1) ;

2) .

Графік диференціальної функції називають нормальною кривою (кривою Гауса) і має вигляд, симетричний відносно прямої , й вісь абсцис є горизонтальною асимптотою кривої.

а

Якщо покласти , то:

— функція Гауса;

— локальна функція Лапласа;

тоді

,

де — нормована змінна.

— таблична функція Лапласа.

Функція розподілу нормального закону має вигляд:

.

а) Імовірність не перевищення заданого значення х :

;

.

б) Імовірність перевищення заданого значення х :

;

.

в) Імовірність прийняття значення в заданому інтервалі:

,

де

;    .

Імовірність того, що Х прийме значення, що належить інтервалу обчислюється за формулою:

,

де — функція Лапласа.

Імовірність того, що абсолютна величина відхилення випадкової величини Х від свого математичного сподівання а менше позитивного числа :

.

Зокрема, якщо , то:

.

Асиметрія, ексцес, мода і медіана нормального розподілу відповідно дорівнюють:

.

Випадкові величини, які розподілені за нормальним законом розподілу, широко поширені в природі. Такими випадковими величинами можуть бути ріст людини, вага пійманої риби, дальність польоту снаряда при стрілянині з якогось одного виду знаряддя й т.д.

Приклад 1. Для нормальної випадкової величини Х з параметрами знайти ймовірність .

Ф(2) – Ф(–0,5) =

= Ф(2) + Ф(0,5) = 0,4772 + 0,1915 = 0,6687.

Приклад 2. Розмір діаметра деталі, що випускає цех, розподілений за нормальним законом з параметрами а = 10 см., .

Знайти ймовірність того, що діаметр навмання взятої деталі потрапить в інтервал 9,9-10,2 см.

Розв’язання. Використаємо формулу

де: .

.

.

За таблицею маємо:

, .

.

Приклад 3. Випадкова величина х розподілена за нормальним законом з параметрами а = 6,5 й . Обчислити ймовірність того, що:

а) значення випадкової величини потрапить в інтервал

б) відхилення значення від середнього не перевищить 4.

Розв’язання.

а) За формулою

,

.

б) За формулою

маємо:

.

Приклад 4. Вважається, що відхилення довжини виготов-лених деталей від стандарту є випадковою величиною, що розподілена за нормальним законом. Стандартна довжина деталі см, а середнє квадратичне відхилення дорівнює .

а) Обчислити ймовірність того, що довжина деталі не перевищить 40,12 см.

.

.

.

б) Обчислити ймовірність того, що довжина деталі виявиться більше 40,7 см.

.

.

.

в) Обчислити ймовірність того, що довжина деталі буде коливатися від 40,12 до 40,7 см.

,

де

; .

.

г) Обчислити ймовірність того, що довжина деталі відхилиться від середнього розміру на 0,5 см.

.

.