Лабораторная работа № 3. Проектирование дискретных фильтров по их аналоговым непрерывным эквивалентам Цель работы

− изучение методик проектирования дискретных фильтров по аналоговым эквивалентам, частотные характеристики которых определяют требования к дискретным фильтрам;

− получение навыков расчета дискретных фильтров на основе: аппроксимации Эйлера; инвариантного преобразования импульсной переходной функции; билинейного преобразования;

− получение навыков расчета дискретных фильтров с использованием пакета MatLab.

Краткие теоретические сведения

Существует несколько подходов к проектированию цифровых фильтров. Один из наиболее распространенных состоит в следующем:

1. Определяют передаточную функцию аналогового фильтра, которая удовлетворяет требованиям частотной обработки сигналов, т.е. заданы интервалы частот задерживания и частот пропускания, заданы допустимые величины амплитудных искажений сигналов в полосе пропускания и задерживания.

2. По заданной передаточной функции определяют дискретную передаточную функцию фильтра , которая удовлетворяет требованиям, предъявленным к фильтру .

Переход от к можно осуществить тремя путями:

аппроксимацией Эйлера;

инвариантным преобразованием импульсной переходной функции;

с помощью билинейного преобразования.

При аппроксимации Эйлера исходные данные аналогового фильтра могут быть заданы в двух вариантах: через дифференциальные уравнения или через передаточные функции. Переход от дифференциального уравнения к разностному, осуществляется путем замены производных соответствующими разностями:

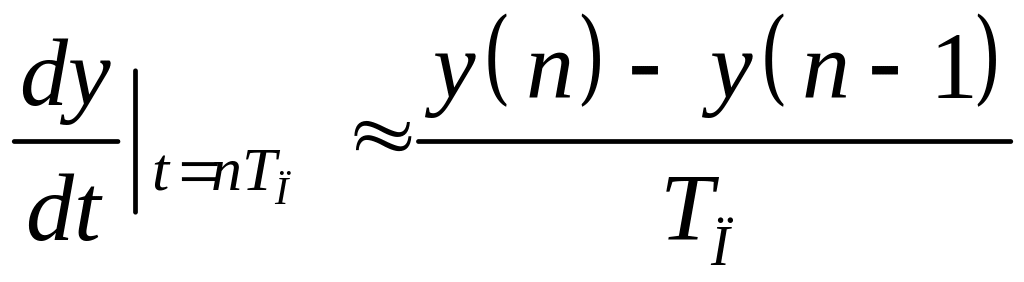(3.1)

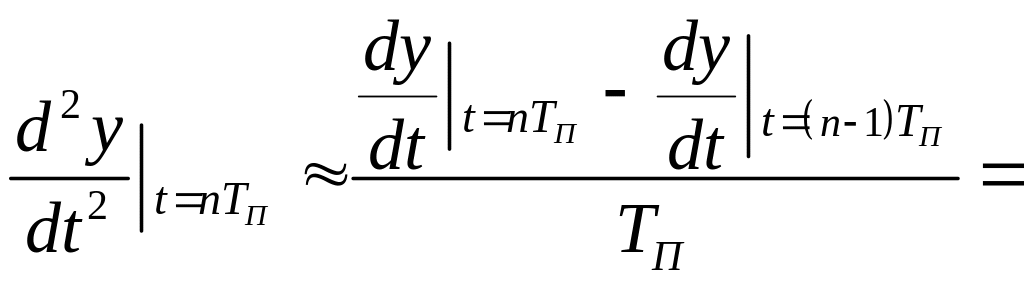
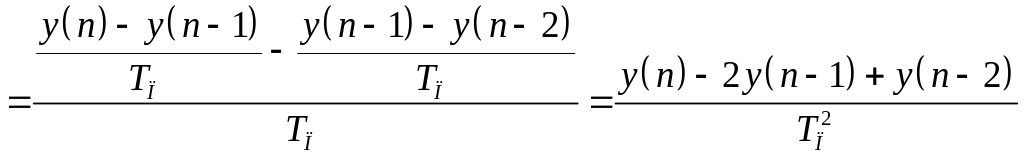
Переход от к можно осуществить, заменив, непрерывный оператор на его дискретный аналог

. (3.2)

Как следует из выражений (3.1) и (3.2) ошибка перехода от непрерывного представления к дискретному зависит от интервала дискретности . Поэтому частотные характеристики дискретного фильтра в полосе пропускания будут приближаться к частотным характеристикам аналогового фильтра только при условии, что интервал дискретизации достаточно мал.

Например, пусть задана передаточная функция фильтра нижних частот

.

Найдем передаточную функцию соответствующего цифрового фильтра. Учитывая соотношение (3.2), получим дискретную передаточную функцию фильтра в виде:

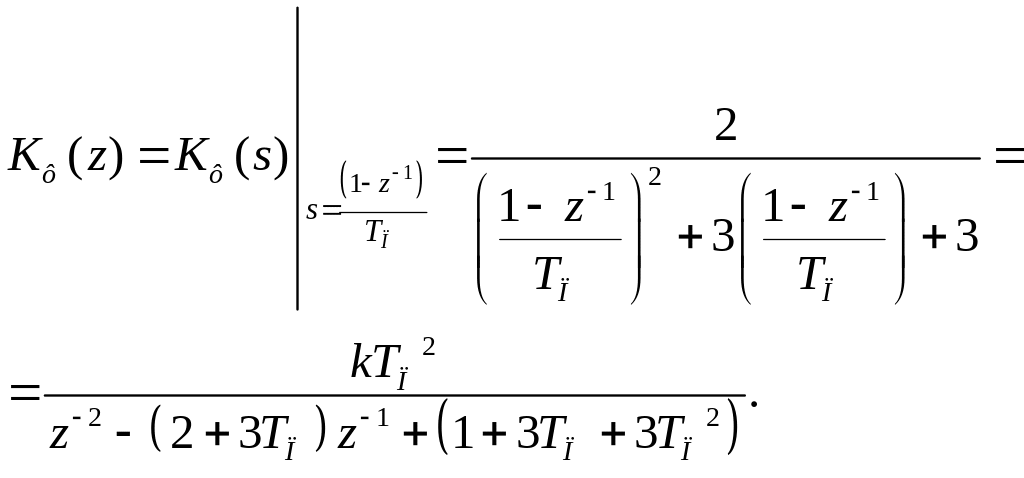(3.3)

При и выражение (3.3) принимает, соответственно, следующие числовые значения

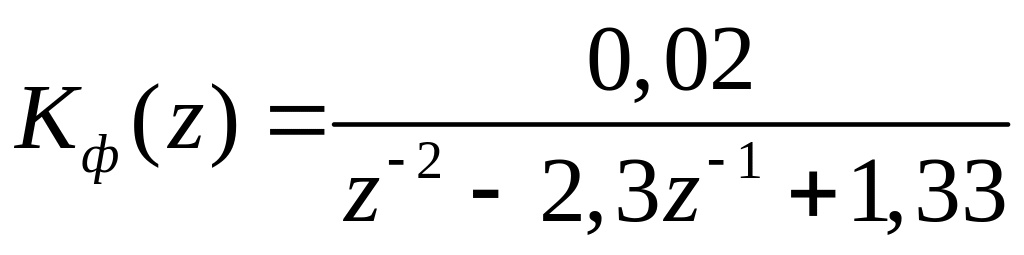, (3.4)

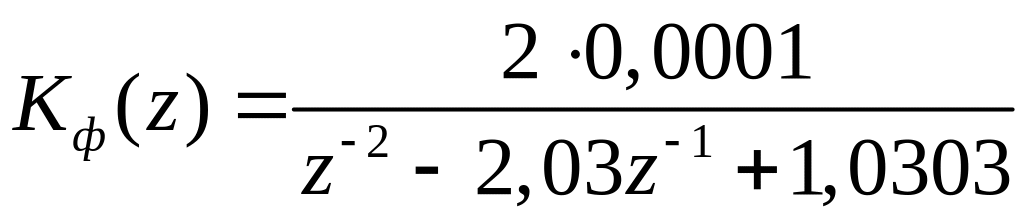. (3.5)

Процесс перехода от непрерывного описания процессов к их дискретному представлению можно упростить с помощью MatLab. Приведем пример программного кода с подробными комментариями и результат его работы (рис 3.1, рис. 3.2.):

h=tf([2],[1,3,3]) %Передаточная функция непрерывного фильтра.

Tp=0.1; %Интервал дискретности.

hd=c2d(h,Tp) %Передаточная функция дискретного фильтра.

syms z s %Ввод символьных переменных.

k=2; %Ввод символьных переменных.

s=(1-z^-1)/Tp %Ввод символьных переменных.

hs=k/(s^2+3*s+3) %Исходное уравнение.

hs1=simplify(hs) %Компактное представление исходных данных.

dd=filt(0.02,[1.33,-2.3,1],Tp) %Передаточная функция дискретного фильтра.

figure(1) %Резервирование первого графического окна.

bode(h,hd,dd), %Логарифмические характеристики: 1-непрерывный фильтр;

%2-дискретный (команда c2d);

%3-аппроксимация Эйлера.

grid on % Включение сетки на графике логарифмических характеристик.

Tp=0.01; %Интервал дискретности 0,01.

syms z s %Ввод символьных переменных.

k=2; %Ввод символьных переменных.

s=(1-z^-1)/Tp %Ввод символьных переменных.

hs2=k/(s^2+3*s+3) %Исходное уравнение.

hs2=simplify(hs2) %Компактное представление исходных данных.

dd2=filt(2*0.01^2,[1.0303,-2.03,1],Tp) %Передаточная функция фильтра

figure(2) % Резервирование второго графического окна.

bode(h,dd,dd2), %Логарифмические характеристики:1-непрерывный фильтр;

%2-дискретный ( );

%3-дискретный ( ).

grid on % Включение сетки на графике логарифмических характеристик

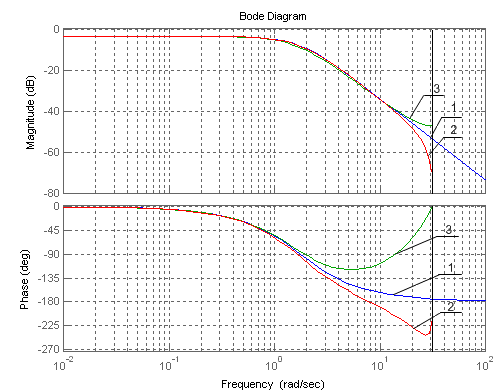
Рис. 3.1. Логарифмические характеристики фильтров (1−аналоговый; 2−дискретный (команда c2d); 3−дискретный (аппроксимация Эйлера))

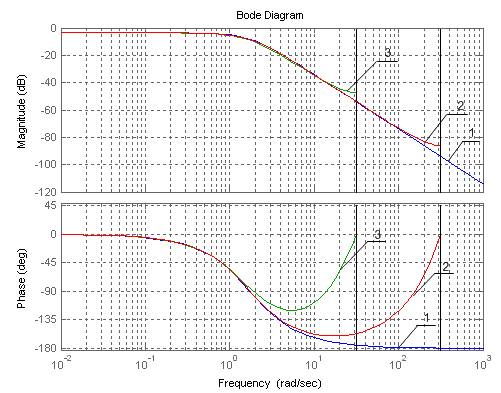
Рис. 3.2. Логарифмические характеристики фильтров (1 − аналоговый; 2 − дискретный при ; 3 − дискретный при )

Из рис. 3.2 следует, что при наблюдается различие, особенно на фазовых характеристиках в области рабочих частот. Под рабочими будем понимать частоты, на которых ослабление сигнала не превышает - . При уменьшении диапазон рабочих частот расширяется и можно утверждать, что различие между частотными характеристиками аналоговых и дискретных фильтров наблюдается только при значительных ослаблениях сигналов (свыше - ).

Второй способ построения цифрового фильтра по аналоговому прототипу заключается в таком преобразовании параметров аналогового фильтра в параметры дискретного фильтра, при котором импульсные характеристики фильтров (аналогового и дискретного) совпадали бы в дискретные моменты времени при .

Математически условие совпадения импульсных характеристик фильтров (аналоговых и дискретных) записывается как

, (3.6)

где , − импульсные характеристики аналоговых и дискретных фильтров, соответственно.

Для нахождения передаточной функции вторым методом определим передаточную функцию аналогового фильтра, а затем представим ее в виде простых дробей

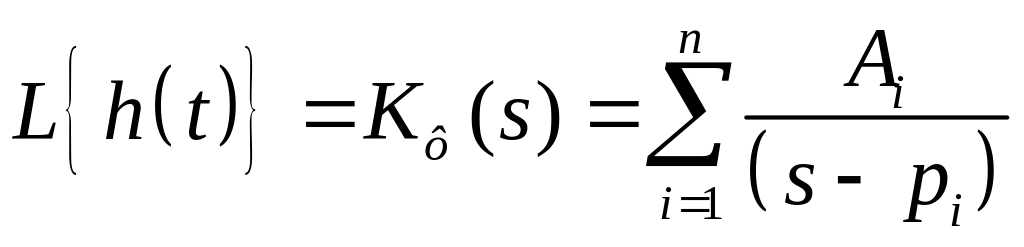. (3.7)

где − различные полюса (корни) передаточной функции аналогового фильтра; − коэффициенты, определенные любым из известных методов; − степень характеристического уравнения знаменателя.

Аналогично уравнению (3.7) могут быть получены соотношения, определяющие передаточную функцию дискретного фильтра (цифрового), которые затем так же можно представить в виде суммы дробей

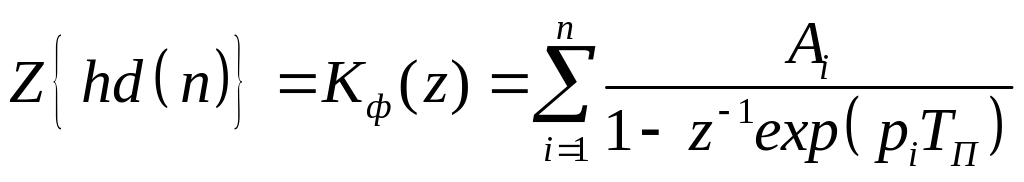, (3.8)

Сравнивая выражения (3.7) и (3.8), получаем соотношение перехода от аналоговых фильтров к цифровым фильтрам по методу инвариантного преобразования импульсной переходной характеристики

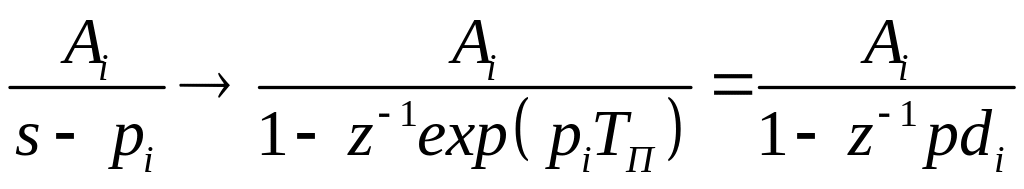, (3.9)

Например, пусть задана передаточная функция аналогового фильтра

.

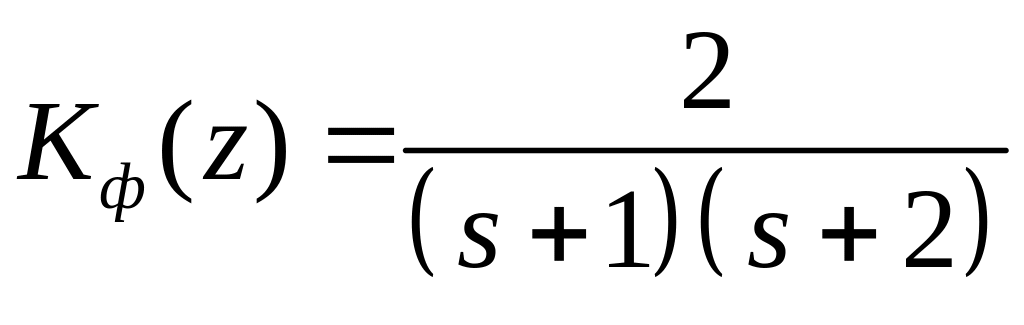Найдем методом инвариантного преобразования импульсной переходной функции цифровой фильтр. Представим передаточную функцию в виде простых дробей

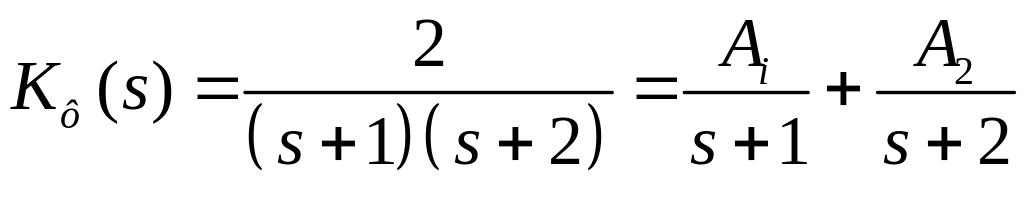. (3.10)

Определим и методом Хевисайда: , .

Используя соотношение (3.9) запишем передаточную функцию цифрового фильтра

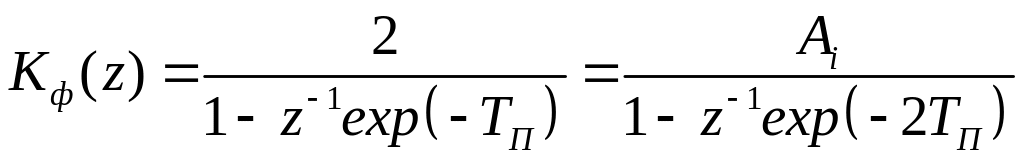. (3.11)

Упрощая выражение (3.11), получим

. (3.12)

При , получим

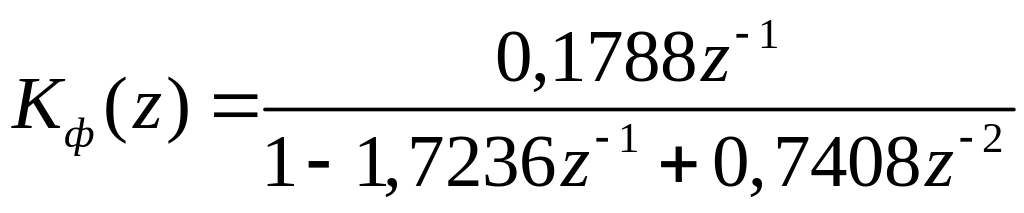. (3.13)

Все трудоемкие вычисления в данном случае можно исключить с помощью процедуры impinvar пакета MatLab:

[bd, ad]=impinvar(b,a,Fs),

где ,  − заданные векторы коэффициентов числителя и знаменателя передаточной функции аналогового прототипа,  − частота дискретизации сигнала в герцах, а , − вычисленные коэффициенты числителя и знаменателя дискретной передаточной функции дискретного фильтра.

Программа определения параметров дискретного фильтра по его аналоговому прототипу, основанная на свойстве совпадения импульсных характеристик обоих фильтров в точках квантования сигналов, представлена ниже:

h=tf([2],[1,3,3]) %Передаточная функция непрерывного фильтра.

Tp=0.1; %Интервал дискретности.

hd=c2d(h,Tp) %Передаточная функция дискретного фильтра.

[n,d,t]=tfdata(h,'v') %Определение коэффициентов передаточной

%функции непрерывного фильтра.

[nd,dd]=impinvar(n,d,10) %Определение коэффициентов передаточной

%функции дискретного фильтра.

f=(filt([0,0.1722],[1,-1.7236,0.7408],0.1)*Tp) %Передаточная функция нормированного

%дискретного фильтра.

bode(h,hd,f),grid on %Логарифмические характеристики

%проектируемых фильтров.

Следует отметить, что усиление цифрового фильтра на нулевой частоте равно , а усиление аналогового фильтра на составляет 1. Поэтому, если сравнить выражение (3.13) с аналогичным выражением, полученным в пакете MatLab, то наблюдается расхождение, определяемое множителем . Чтобы привести в соответствие результаты расчетов, полученные аналитическим путем (выражения 3.10-3.13) с результатами расчетов, полученными в пакете MatLab, следует пронормировать выражение (3.13), умножив его на значение интервала дискретности.

Результаты выполнения данной программы показывают, что передаточные функции, полученные путем трудоемких расчетов (выражения 3.10-3.13) и с помощью процедуры impinvar, совпадают. Логарифмические характеристики, полученные применением разных процедур, отличаются: меньшую ошибку дает процедура impinvar.

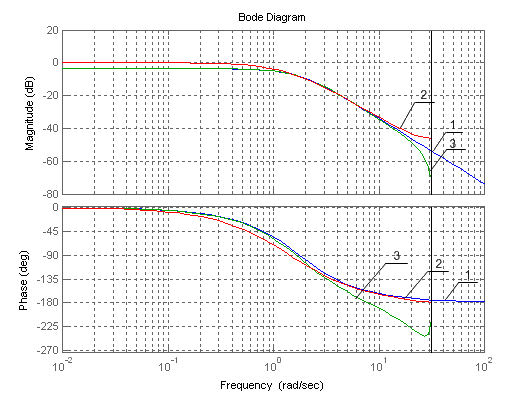
Рис.3.3. Логарифмические характеристики фильтров (1 - аналоговый; 2−дискретный (процедуры impinvar); 3 - дискретный (процедуры c2d)).

Известно, что метод преобразования импульсной переходной функции базируется на связи точек плоскости s с точками плоскости z, определяемой отношением

, (3.14)

где  − угол между действительной осью плоскости s и векторами, определяющими точки на окружности единичного радиуса плоскости z.

Из (3.14) следует, что связь между точками плоскости s и z неоднозначна и вносит эффект наложения, что может исказить результаты вычислений, т.е. синтезированный таким образом цифровой фильтр не будет адекватен его аналоговому прототипу. Действительно, частоты , и на плоскости z отображаются в одну точку – .

Для исключения нежелательного эффекта наложения вводят билинейное преобразование, которое однозначно преобразует точки мнимой оси плоскости s в точки мнимой оси плоскости w. Таким образом, переход от мнимой оси плоскости s на плоскость z осуществляется в два этапа. Выражение (3.14) преобразует мнимую ось плоскости s в окружность единичного радиуса плоскости z, а выражение (3.15) преобразует мнимую ось плоскости s в мнимую ось плоскости w и известно также как w- преобразование

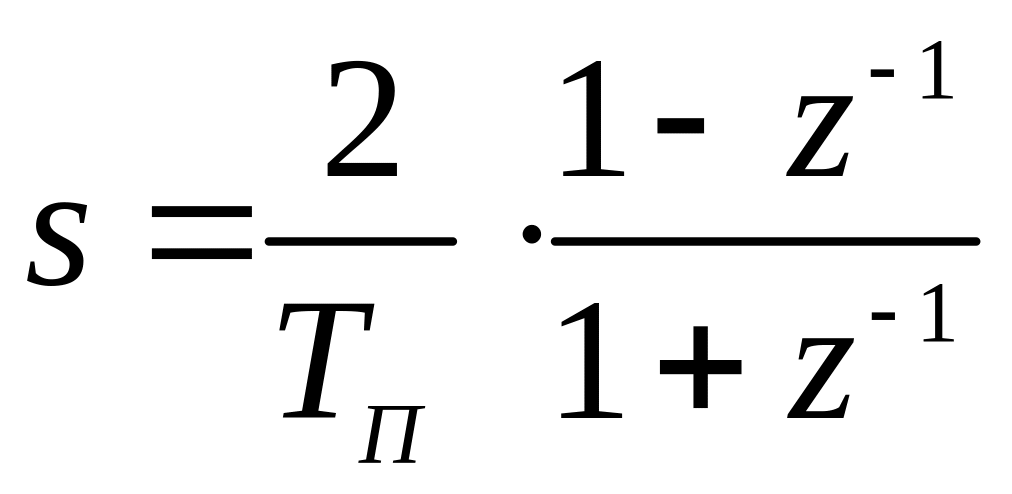. (3.15)

Решая уравнение (3.15) относительно z получим выражение, определяющее обратный переход из плоскости w в плоскость s:

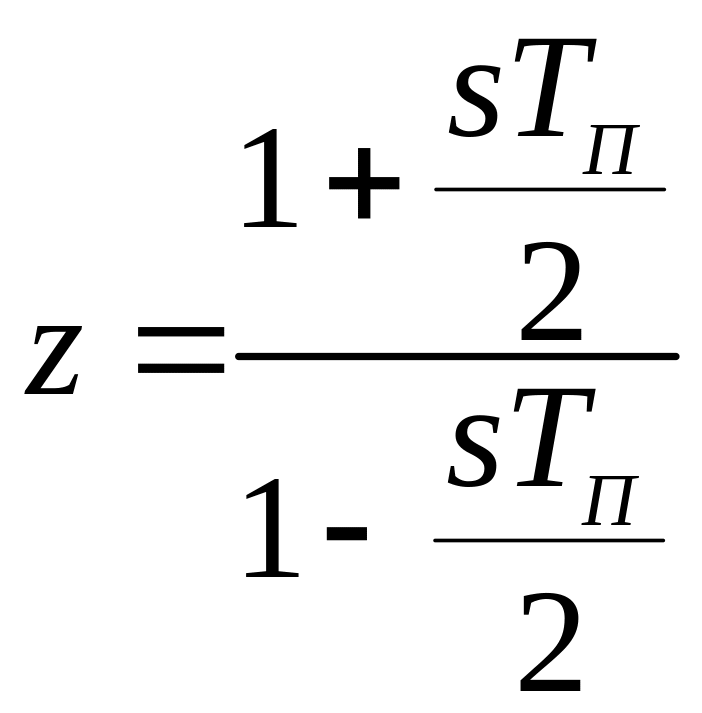. (3.16)

Используя соотношения (3.15-3.16) опишем методику расчета цифровых фильтров, которая в целом не отличается от рассмотренной ранее и состоит из следующих шагов.

1. Исходя из технических требований, определяют передаточную функцию требуемого аналогового фильтра .

2. Применяют к билинейное преобразование и получаем передаточную функцию цифрового фильтра

. (3.17)

При преобразовании (3.17) будет сохраняться вид частотных характеристик и свойства устойчивости аналогового фильтра. Однако это не означает, что частотные характеристики аналогового и цифрового фильтров полностью одинаковы, совпадает только их форма. Например, если АЧХ аналогового фильтра убывает монотонно при изменении частоты от 0 до , то АЧХ цифрового фильтра будет монотонно убывать при изменении цифровой частоты от 0 до ; и аналогично, если АЧХ аналогового фильтра имеет подъемов и спадов в частотном диапазоне от 0 до , то и АЧХ соответствующего цифрового фильтра будет иметь подъемов и спадов в диапазоне цифровой частоты от 0 до . Отметим, что связь между и нелинейная:

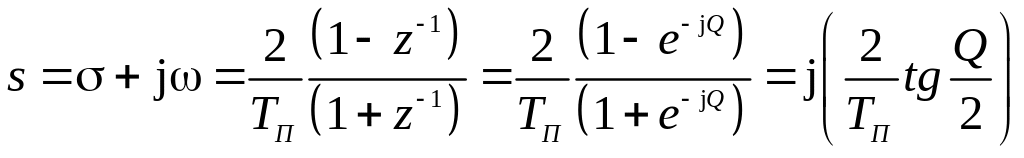, (3.18)

. (3.19)

Анализируя выражения (3.18) и (3.19) можно сделать выводы: связь между цифровой частотой и аналоговой частотой взаимообратная, т. е. по заданной круговой частоте можно определить цифровую частоту, а по заданной цифровой частоте можно определить круговую частоту.

Изменяя интервал дискретности, можно менять коэффициент пропорциональности между и (3.19), что позволяет изменять формы АЧХ цифровых фильтров.

Например, пусть задана передаточная функция аналогового фильтра . Используя (3.17) определим передаточную функцию цифрового фильтра

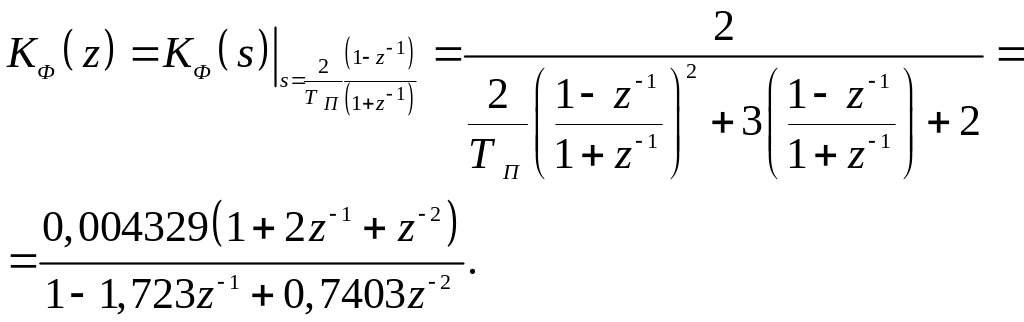(3.20)

Процедуру определения параметров цифрового фильтра на основе метода билинейного преобразования можно упростить, воспользовавшись процедурами bilinear или c2d пакета Matlab.

К процедуре bilinear можно обратиться тремя путями

[bd, ad] = bilinear(b, a, Fs, Fp); (3.21)

[zd, pd, kd]=bilinear(z, p, kFs, Fp); (3.22)

[Ad, Bd, Cd, Dd]=bilinear(А, В, С, D, Fs, Fp). (3.23)

Исходные данные для выполнения процедуры bilinear – это параметры аналогового фильтра, заданные в любой форме lti-модели. Параметр Fs задает частоту дискретизации в герцах. Параметр не обязателен, он определяет частоту в герцах, для которой значения АЧХ до и после выполнения преобразования должны совпадать.

Выражения (3.21)-(3.23) отличаются исходными данными. В (3.21) будут определяться коэффициенты числителя и знаменателя дискретного фильтра по коэффициентам числителя и знаменателя аналогового прототипа. В выражении (3.22) исходными данными аналогового прототипа являются нули z, полюса р, и коэффициент усиления . Обращение к выражению (3.22) позволяет вычислить нули zd, полюса pd и коэффициент усиления kd дискретного фильтра. И, наконец, выражение (3.23) определяет дискретные матрицы пространства состояния дискретного фильтра по известным непрерывным матрицам пространства состояния аналогового фильтра.

Процедура c2d определяет параметры дискретного фильтра по непрерывной передаточной функции h и интервалу дискретности :

hd = c2d(h, Tp, 'метод'). (3.24)

MatLab предлагает несколько методов аппроксимации: нулевого порядка, первого порядка, метод билинейной аппроксимации Тастина, билинейной аппроксимации Тастина с коррекцией и метод соответствия нулей и полюсов. При выборе метода аппроксимации выражение (3.24) конкретизируется. Например, если применена билинейная аппроксимации Тастина, то записывают

hd = c2d(h, Tp, 'TUSTIN'). (3.25)

Логарифмические характеристики дискретных фильтров на рис. 3.4 получены в результате выполнения следующей программы:

h=tf([2],[1,3,2]) %Исходные данные

syms z s %Ввод символьных переменных

k=2; %Числовые значения символьных переменных.

Tp=0.1;

s=(2/Tp)*(1-z^-1)/(1+z^-1) %Переход на плоскость w.

hs=2/(s^2+3*s+3) %Применение преобразования к аналоговому фильтру.

hs1=simplify(hs) %Алгебраические преобразования

hs2=filt([1,2,1],[1,-794/463,343/463],Tp)*(2/463) %Уравнение

%цифрового фильтра при билинейном преобразовании.

[n,d,t]=tfdata(h,'v') % Определение коэффициентов

%передаточной функции непрерывного фильтра.

[nd,dd]=bilinear(n,d,10) % Определение коэффициентов дискретного фильтра

% при билинейном преобразовании.

Tp=0.1;

hdt=c2d(h,Tp,'TUSTIN') %Уравнение цифрового фильтра при

%преобразовании Тастина.

hdv=filt(nd,dd,Tp) %Уравнения к форме фильтра.

bode(h,hdt,hdv), grid on %Логарифмические характеристики

% аналоговых и цифровых фильтров.

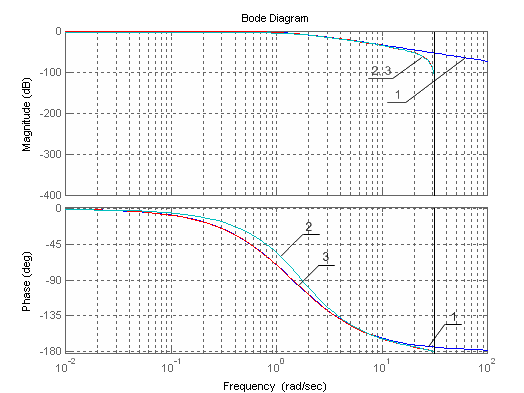
Рис.3.4. Логарифмические характеристики фильтров (1-аналоговый; 2-дискретный (процедура билинейного преобразования); 3 - дискретный (процедуры c2d))

Из результата расчета следует, что графики частотных характеристик, полученные путем трудоемких расчетов (выражение (3.20)) и с помощью процедур bilinear и c2d, совпадают. Учитывая, что процедуры bilinear и c2d равнозначны, но в c2d исходные данные задаются в более удобном виде, то ее целесообразно использовать при расчете цифровых фильтров методом билинейной аппроксимации.