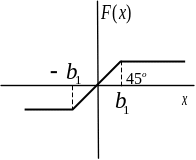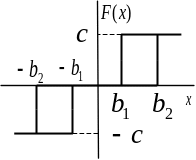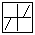Лабораторная работа № 4. Исследование нелинейных сау Цель работы

– построение моделей нелинейных систем в пакете Simulink;

– исследование влияния различных видов НЭ на выходные характеристики линейных систем первого, второго и третьего порядков;

– исследование возникновения и устойчивости автоколебаний нелинейных систем в зависимости от параметров линейной части, амплитуды и частоты входного воздействия.

Краткие теоретические сведения

Большинство реальных систем содержат разного рода нелинейные элементы, изменяющие характер работы системы и придающие ей новые свойства. В то время как устойчивость линейных систем определялась лишь характеристиками входящих в них элементов, устойчивость и качество процессов нелинейных систем зависит также от величины сигналов и величины начальных условий.

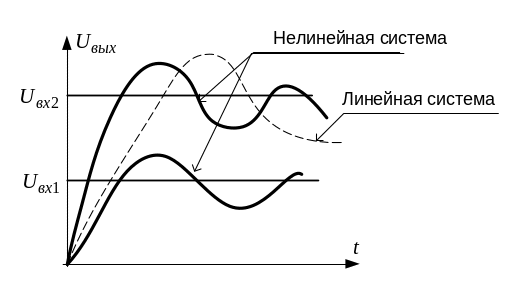
Рисунок 4.1. – Отличие переходных процессов нелинейных и линейных систем

Таким образом, нелинейная система, устойчивая в малом (при малых воздействиях), может оказаться неустойчивой в большом. Помимо сходящихся и расходящихся переходных процессов, в нелинейных системах могут возникать устойчивые автоколебания – периодическое движение системы, самопроизвольно возникающее при ее включении. Такие колебания – результат внутренних свойств системы, обусловленных наличием нелинейного элемента. Для нелинейных систем не выполняется принцип суперпозиции.

В табл. 4.1 приведены статические характеристики основных типов нелинейных элементов (НЭ), рассматриваемых в ТАУ, и блоки, с помощью которых НЭ моделируются в Simulink (библиотека Discontinuities). Табл. 4.2 содержит графические изображения и основные параметры соответствующих блоков Simulink.

Таблица 4.2  Виды нелинейных элементов

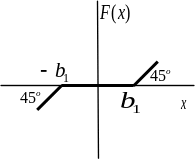
(Насыщение  Saturation)	(Зона нечувствительности  Dead Zone)
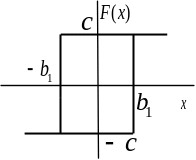
(Трехпозиционное реле с гистерезисом  Relay+Relay)	(Реле с гистерезисом  Relay)
(Трехпозиционное реле  Relay+Relay)	(Двухпозиционное реле  Relay)

Таблица 4.2  Модели нелинейных звеньев в Simulink

	Saturation – насыщение, в параметрах задаются верхний и нижний пределы (Upper limit и Lower limit).
	Dead zone – нечувствительность, «мертвая зона». В параметрах задаются пределы нечувствительности (Start of dead zone и End of dead zone).
	Relay – реле, в параметрах задаются точки переключения (Switch on point и Switch off point), в также величины сигналов в режимах «включено» (Output when on) и «выключено» (Output when off).

Динамика нелинейных систем описывается нелинейными дифференциальными уравнениями, которые не имеют общего решения. Поэтому большую роль при исследовании нелинейных систем приобретают различные приближенные методы расчета и методы моделирования.

Реальные нелинейные САУ содержат различные комбинации НЭ. Однако универсальный учет всех нелинейностей чрезвычайно затруднителен и на практике нецелесообразен, поскольку преобладающее влияние имеет лишь одна-две нелинейности. Большинство реальных систем может быть приведено к виду, который изображен на рис. 4.2. где обозначено – нелинейный элемент, – передаточная функция линейной части системы.

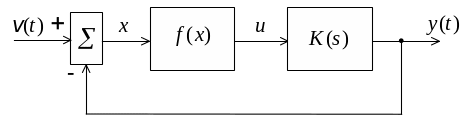
Рисунок 4.2. – Структурная схема нелинейной системы

Наиболее распространенным инженерным методом анализа нелинейных САУ является метод гармонической линеаризации. Сущность метода заключается в замене НЭ линейным, таким, чтобы его выходной сигнал соответствовал первой гармонике сигнала на выходе нелинейного элемента. Такой способ линеаризации возможен и правомерен, только тогда, когда линейная часть системы представляет собой фильтр низких частот, не пропускающий высшие гармоники. Обычно в реальных САУ такое условие выполняется за счет работы НЭ в контуре с линейной передаточной функцией.

Коэффициент гармонической линеаризации для неоднозначных нелинейностей представляет собой комплексную величину, определяемую выражениями:

; (4.1)

; (4.2)

, (4.3)

где S – площадь петли неоднозначного нелинейного элемента. Для рассматриваемых в лабораторной работе видов НЭ гармонические коэффициенты линеаризации приведены в табл. 2.4.

Условия возникновения автоколебаний и их параметры следуют из уравнения гармонического баланса

. (4.4)

Широко распространен графический метод решения уравнения гармонического баланса (метод Гольдфарба). Для этого на комплексной плоскости строят амплитудно-фазовую характеристику (АФХ) линейной части и обратную гармоническую характеристику нелинейного элемента

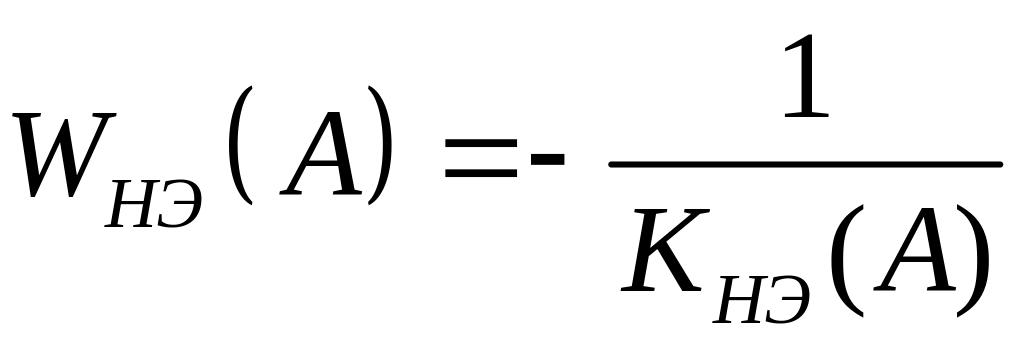. (4.5)

Пересечение этих кривых указывает на возможность возникновения автоколебаний (рис. 4.3).

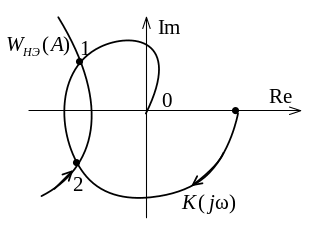
Рис. 4.3. Иллюстрация способа Гольдфарба

При этом, если, перемещаясь по кривой в сторону возрастания амплитуд, выходим из контура, охваченного , то точке пересечения соответствуют устойчивые автоколебания (точка 1), а если входим в контур, – неустойчивые (точка 2). В точке устойчивых автоколебаний определяется частота автоколебаний по кривой и амплитуда автоколебаний по кривой . Точка неустойчивых автоколебаний разграничивает режимы работы системы в зависимости от начальных условий.

Если кривые и нигде не пересекаются, то система либо устойчива в целом – целиком расположена вне контура, охваченного , либо в противном случае неустойчива.

В системе с однозначными статическими характеристиками нелинейных элементов удобно для анализа устойчивости и автоколебаний использовать логарифмические характеристики (рис. 2.4). При этом частоту автоколебаний определяют из условия баланса фаз

, (4.6)

а амплитуду из условия баланса амплитуд

, (4.7)

где – логарифмическая гармоническая характеристика нелинейного элемента.

Рисунок 4.4 – Использование ЛАЧХ для анализа устойчивости автоколебаний

Для проверки устойчивости автоколебаний необходимо дать небольшое приращение амплитуде относительно исследуемой точки и путем обратного перестроения возвратиться к фазовой характеристике. Если при этом запас устойчивости по фазе существует, то автоколебания в исследуемой точке устойчивы (точка 2 рис. 4.4).

В лабораторной работе исследуются замкнутые системы с передаточными функциями вида 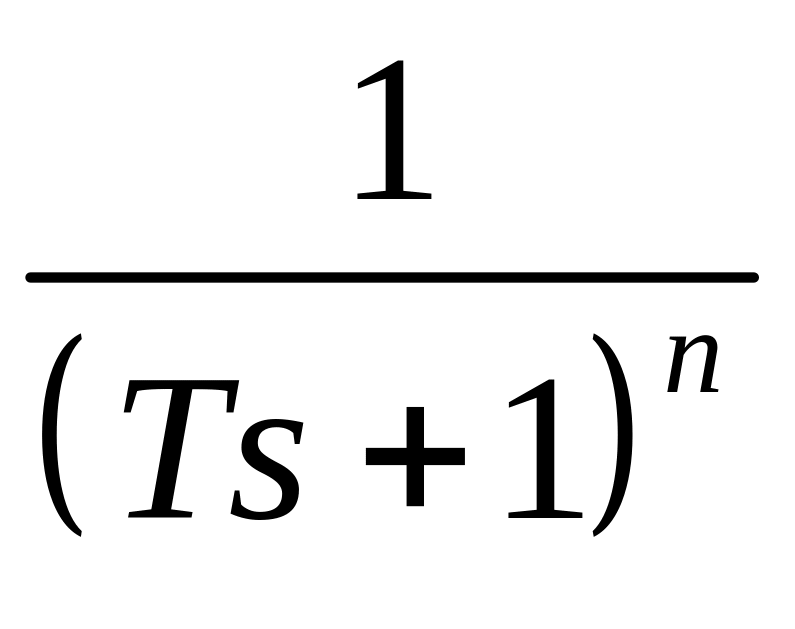, где (n=1,2,3) и различными видами нелинейных элементов.