8.2. Исследование нелинейных систем на фазовой плоскости

Метод фазовой плоскости используется для исследования нелинейных САУ, линей­ная часть которых с достаточной для решения практических задач точностью может быть описана диффе­ренциальным уравнением второго порядка.

Фазовой плоскостью называется плоскость, на кото­рой изображается изменение какой-либо переменной ве­личины в функции скорости ее изменения:. Оси времени на фазовой плоскости нет, но каждому моменту времени соответствует определенная точка (изображающая точка), абсцисса и ордината которой равны соответственно значению сигнала и скорости его изменения в данный момент времени. При изменении времени изображающая точка перемещается по определенной траектории, называемой фазовой траекторией.

Определим выражение фазовой траектории для сигнала , представляющего собой незатухающие гармониче­ские колебания с амплитудой и частотой(рис. 8.6, а):

. (8.1)

Скорость изменения такого сигнала равна:

. (8.2)

Выражая из уравнений (8.1) и (8.2) и, на основании основного тригонометрического тождества получим:

. (8.3)

Следовательно, незатухающие гармонические колеба­ния изображаются на фазовой плоскости в виде эллипса (рис. 8.6, б) с полуосями А и .

При изменении времени изображающая точка, будет перемещаться вдоль эллипса по часовой стрелке с периодом колебания .

Для различных амплитуд А при заданной частоте можно построить семейство таких эллипсов, вложенных один в другой (рис. 8.6, в). Совокупность фазовых траекторий нелинейной системы, соответствующих различным значения ее параметров или начальных условий, называетсяфазовой картиной (фазовым портретом).

Вслучае расходящегося колебательного процесса (рис. 8.7, а) амплитуда колебаний увеличи­вается и соответствующая такому процессу фазовая траектория бу­дет иметь вид расходящейся логарифмической спирали (рис. 8.7, б). Наоборот, затухающий колебательный процесс (рис. 8.8, а) на фазовой плоскости изображается в виде логарифмической спирали, сходящейся к началу коорди­нат (рис. 8.8, б). Фазовые портреты, соответствующие различным значениям начальных условий для таких процессов приведены соответственно на рис. 8.7, в и рис. 8.8, в.

Таким образом, по виду фазовой траектории можно наглядно судить об устойчивости си­стемы.

Возможно и решение обратной задачи – определение закона изменения сигнала по уравнению фазовой траектории. Пусть, например, фазовая траектория представляет собой отрезок прямой, начальная точка (соответствующая моменту времени) которого имеет координаты (), а конечная совпадает с началом координат фазовой плоскости. Очевидно, что уравнение фазовой траектории:

где .

На рис. 8.9, а приведена совокупность таких фазовых траекторий, различающихся значениями абсциссыи ординатыначальной точки для случая, когда знакиипротивоположны ( 0), а на рис. 8.9, б – когда знаки исовпадают ( 0).

Так как то уравнение фазовой траектории можно записать в виде:. Разделяя переменные, имеемИнтегрируя последнее выражение, получим:

= = .

Откуда и, следовательно, искомый закон изменения сигнала:

.

Совокупность графиков сигнала, соответствующих различным начальнымусловиям для случая  0, представлена на рис. 8.9, в, а для случая  0 – на рис. 8.9, г.

Аналитическое выражение для закона изменения сигнала по уравнению фазовой траектории удается определить в очень редких случаях. Но приблизительный графикможно построить, воспользовавшись следующей методикой. Необходимо, начиная от начальной точки (), отметить на фазовой траектории (рис. 8.10, а) точки, абсциссы которых отличаются друг от друга на достаточно малое постоянное по величине приращение. При этом время перехода системы от одной такой точки к достаточно близкой соседней может быть приближенно определено по формуле:

, (8.4)

где – среднее значение скорости изменения сигнала, определяемое как ордината середины отрезка фазовой траектории между данными точками. Построение графиканачинается с точки, находящейся на оси ординат (рис. 8.10, б).

Каждая последующая точка графика отличается от предыдущей: по оси абсцисс на величину, а по оси времени – на величину, рассчитываемую для каждого перехода по выражению (8.4).

Рассмотрим общие закономерности, которым удовлетворяют фазовые траектории нелинейных систем.

Поскольку в верхней полуплоскости фазовой плоскости , то изображающая точка движется вдоль фазовой тра­ектории в сторону увеличения . В нижней по­ловине, следовательно, изображающая точка дви­жется вдоль фазовой траектории в сторону уменьшения. Так как в точках пересечения фазовых траекторий с осьюпроизводная, то фазо­вые траектории пересекают ось х под прямым углом.

Между собой фазовые траектории пересекаются только в особых точках. Особыми точками называют точки, соответствующие состоянию равновесия системы. Особые точки бывают четырех видов: центр, фокус, узел и седло. Центром называется особая точка в начале координат (на рис. 8.6, в). Особая точка в начале координат (см. рис. 8.7, в) является неустойчивым фокусом или устойчивым фокусом (см. рис. 8.8, в).

Начало координат являетсяустойчивым узлом, если фазовые траектории входят в него (см. рис. 8.9, а), и неустойчивым узлом в противоположном случае (рис. 8.9, б). Находящаяся в начале координат особая точка типа «седло» всегда неустойчива, т.е. соответствует неустойчивому состоянию равновесия (рис. 8.11, а). На рис. 8.11, б особые точки образуют особый отрезок, в каждой точке которого возможно равновесие системы.

Незатухающим колебаниям в нелинейной системе на фазовой плоскости соответствуют замкнутые траектории – предельные циклы. Они бывают устойчивыми и неустойчивыми.

Устойчивый предельный цикл описывает на фазовой плоскости режим автоколебаний в системе. Он характерен тем, что фазовые траектории с обеих сторон от устойчивого предельного цикла «наматываются» на него (рис. 8.12, а).

В случае неустойчивого предельного цикла фазовые траектории отдаляются от него с одной или с обеих сторон (рис. 8.12, б). Неустойчивый предельный цикл соответствует неустойчивым колебаниям, которые в реальных системах не существуют. При этом неустойчивый предельный цикл определяет на фазовой плоскости границу, разделяющую различные установившиеся режимы.

Рассмотрим пример построения фазового портрета нелинейной САУ (рис. 8.13). Пусть передаточная функция линейной части системы равна:

, (8.5)

а статическая нелинейная зависимость между входным и выходным сигналом нелинейного элемента:

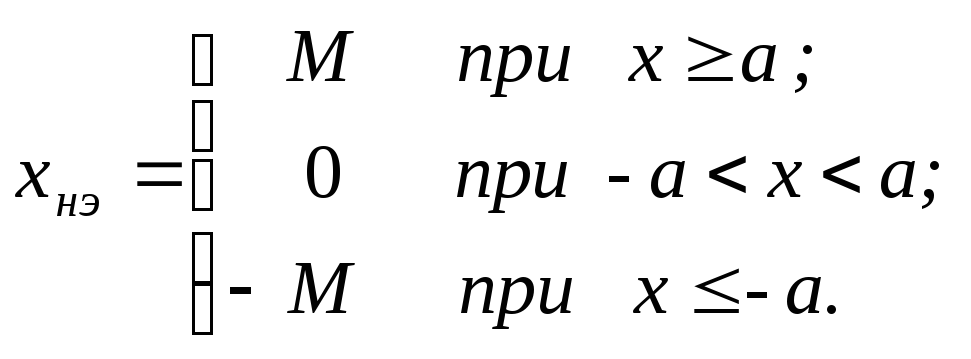(8.6)

Такая статическая зависимость соответствует типовому нелинейному элементу «однозначная релейная характеристика с зоной нечувствительности».

Описание системы будем осуществлять в ее свободном движении, т.е. полагать, что, при этом.

Изображение по Лапласу выходного сигнала системы равно:

. (8.7)

Соответствующее выражению (8.7) операторное уравнение имеет вид:

или

(8.8)

Выполнив для (8.8) обратное преобразование Лапласа, получим:

. (8.9)

В дальнейшем для упрощения аргумент t опускается.

С учетом выражений (8.6) и (8.9) можно записать следующие дифферен­циальные уравнения, определяющие переходный процесс в системе в трех зонах величины :

(8.10)

Наиболее просто выводится уравнение фазовой траектории для второй зоны (при ). Так каки, то дифференциальное уравне­ние для этой зоны можно записать следующим образом:

или .

Разделив последнее выражение на равенство , получим:

или .

Интегрируя последнее уравнение, находим:

, (8.11)

где – постоянная интегрирования.

При различных значениях на участке –а < х < а фазовый портрет системы представляет собой семейство параллельных прямых, угол наклона которых к оси абсцисс определяется величиной постоянной времени .

В первой зоне (при ) дифференциальное уравнение, описывающее поведение системы, имеет вид:

.

С учетом порядок этого дифференциального уравнения может быть понижен:

или .

Разделив последнее уравнение на , получим:

или .

Проинтегрировав это уравнение, получим:

. (8.12)

Постоянная интегрированияможет быть найдена из начальных условий:

,

где () – координаты точки, с которой начинается построение фазовой траектории:

.

Подставляя в выражение (8.12) различные сочетания значений начальных условий , полу­чим семейство фазовых траекторий для диапазона значений регу­лируемой величины .

Семейство фазовых траекторий для диапазона третьей зоны () получим из уравнения (8.12), заменив в нем величину M на –M :

. (8.13)

Для рассматриваемой системы все фазовые траектории, описываемые выражениями (8.12) – (8.13), имеют вид логарифмических спиралей, сходящихся к началу координат.

Полная фазовая картина процесса автоматического регулирова­ния нелинейной системы, динамические свойства которой определяются дифференциальными уравнениями (8.10), имеет вид, представленный на рис. 8.14. Для других систем вид фазовых траекторий может быть иным. Например, на рис. 8.15 изображе­на фазовая картина для нелинейной системы с той же передаточной функцией линейной части, что и в предыдущем примере, но для случая, когда включенный в систему релейный элемент не имеет зоны нечувствительности, т.е.

(8.14)

Далеко не всегда при исследовании системы на фазовой плоскости удается получить аналитическое выражение для фазовых траекторий. В то же время для любой системы, линейная часть которой описывается дифференциальным уравнением второго порядка, можно записать следующее уравнение:

которое может быть сведено к системе дифференциальных уравнений первого порядка:

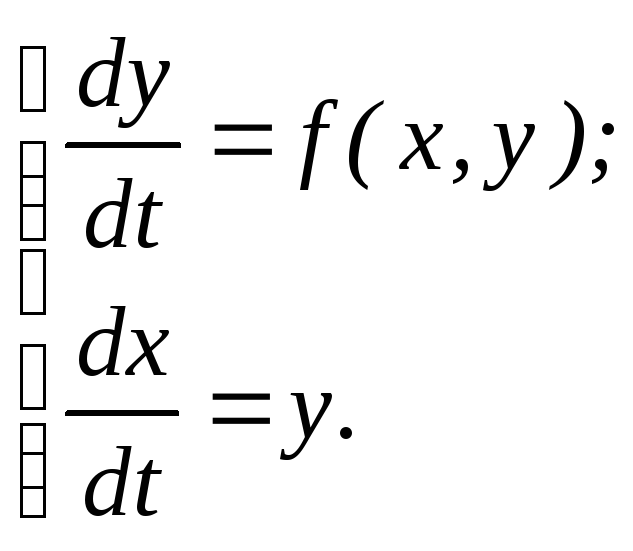(8.15)

Разделив первое уравнение системы (8.15) на второе, получим уравнение фазовой траектории в виде нелинейного дифференциального уравнения первого порядка:

. (8.16)

Построение фазовых траекторий в общем случае не требует решения этого уравнения и может быть выполнено методом изоклин. С этой целью на фазовой плоскости строят семейство изоклин-линий, соответствующих алгебраическому уравнению

, (8.17)

где – постоянная величина, для которой задается ряд произвольных значений от –до +.

Каждому значению Ссоответствует своя изоклина. Как следует из выражения (8.17) для каждой изоклины выполняется равенство:

,

т.е. изоклина представляет собой геометрическое место точек, в которых наклон фазовой траектории постоянен.

На рис 8.16 иллюстрируется методика построения фазовой траектории по нанесенному на плоскость семейству изоклин. На каждой изоклине стрелкой указан наклон (направление касательной), соответствующий значению. Из произвольно выбранной начальной точки с координатами (), находящейся на изоклине, проводятся два луча с наклонами, соответствующими значениями. Затем до пересечения со следующей изоклинойпроводится биссектриса угла, образованного указанными лучами. Точка пересечения с координатами () – очередная точка фазовой траектории, из которой осуществляются аналогичные построения.

По фазовой картине САУ можно судить об устойчи­вости системы и характере переходных процессов ней.