2. Математическое описание линейных сау

2.1. Составление и линеаризация дифференциальных уравнений сау

Процессы, происходящие в САУ, в общем случае описываются нелинейными дифференциальными уравнениями, которые могут быть решены лишь в отдельных редких случаях. Однако для достаточно большого числа систем эти уравнения с приемлемой для решения практических задач точностью могут бытьзаменены линеаризованными.

Рассмотрим принцип линеаризации на примере системы, у которой входнойи выходнойсигналы связаны нелинейной статической зависимостью. Пусть в установившемся режиме величина входного сигнала равнаи его отклонения от этого значения в переходных процессах достаточно малы.

Разложив нелинейную зависимость в ряд Тейлора в окружности точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получим следующую приближенную зависимость:

, (2.1)

где - значение производной функциипопри подстановке в выражение этой производной значения=.

В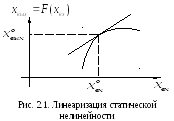ыражение (2.1) можно переписать в виде:

, (2.2)

где ;;

.

Проведенная линеаризация имеет простую графическую интерпретацию: она соответствует (рис. 2.1) замене действительной нелинейной характеристики касательной к ней в точке, соответствующей установившемуся режиму. Коэффициент k в выражении (2.2) равен тангенсу угла наклона этой касательной относительно оси . Поэтому его величина может быть найдена простым графическим построением без нахождения аналитического выражения нелинейной зависимостии ее производной.

В более общем случае, система описывается нелинейным дифференциальным уравнением, связывающим производные по времени входного и выходного сигналов:

.

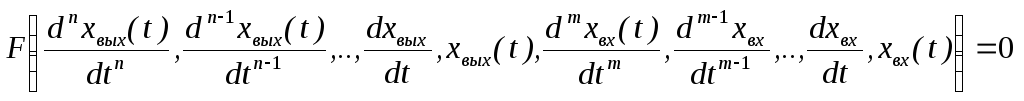(2.3)

Разложив нелинейную функцию (2.3) в ряд Тейлора в точке установившегося движения, получим следующее линейное дифференциальное уравнение для приращения переменных:

….+…

+……….., (2.4)

где ..,и т.д. – значения производных функции (2.3) полученные при подстановке значений входного и выходного сигналов, соответствующих установившемуся режиму.

Следовательно, процедура линеаризации нелинейных систем дает возможность описать их линейными дифференциальными уравнениями в отклонениях. Очевидно, что допустимость такой линеаризации ограничена требованием к незначительности отклонений сигналов от их установившихся значений. Кроме того, поскольку такая линеаризация основана на разложении в ряд Тейлора, она применима только к непрерывно дифференцируемым нелинейностям.

Нелинейные звенья и системы, не удовлетворяющие этому требованию, называются существенно нелинейными. К существенно нелинейным звеньям относятся звенья с прерывистыми характеристиками, например, звенья с релейными характеристиками или неоднозначными характеристиками типа петли гистерезиса.

2.2. Основные свойства преобразования Лапласа. Операторные уравнения сау. Передаточные функции линейных звеньев и систем

В общем случае дифференциальное уравнение, связывающее изменение во времени входной и выходной сигналы линеаризованной системы, имеет следующий вид:

(2.5)

Решение дифференциальных уравнений (2.3) – (2.4) зачастую связа­но со значительными трудностями, а во многих случа­ях, например в следящих системах, не может быть осу­ществлено, так как неизвестно управляющее воздейст­вие. По этим причинам исследование систем ведется косвенными методами, например, базирующимися на операционном преобразовании Лапласа.

Приведем основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

Преобразованием Лапласа называют интегральное преобразование:

, (2.6)

определяющее соответствие между функцией вещественного переменного (в рассматриваемой теории – функцией времени) и функциейкомплексного переменного. При этомназываюторигиналом, а –изображением или изображением по Лапласу. Символическая запись такого преобразования:

=,

где – оператор преобразования Лапласа.

Предполагается, что функция времени , которая подвергается преобразованию Лапласа, обладает следующими свойствами:

• определена и дифференцируема на всей положительной числовой полуоси ;

• = 0 при ;

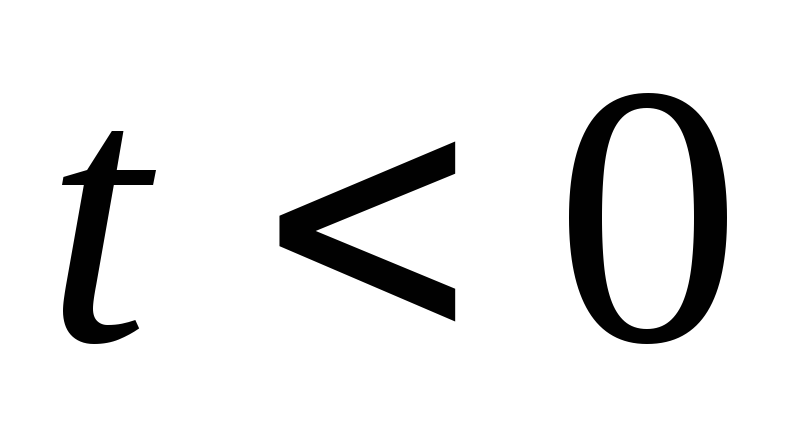• существуют такие числа М и , чтопри.

Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами.

Соотношение

=, (2.7)

определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль прямой Re p = . Символически обратное преобразование Лапласа можно записать так:

=,

где – символ обратного преобразования Лапласа.