9060_d71504bbdcb8f95ffb66490c84b51bf8

В частном случае a = b = c = R получаем уравнение сферы с центром в начале координат: x2 + y2 + z2 = R2.

Уравнение сферы с центром в т. С (x0, y0, z0) приводилось в п. 3.2.1.

5.4.Гиперболоиды

5.4.1.Однополостный гиперболоид

Поверхность, определяемая уравнением x2 + y2 - z2 = 1. a2 b2 c2

ìïx = 0,

В сечении плоскостью x = 0 имеем гиперболу í y2 - z2 = 1;

ïîb2 c2

в сечении z = h — эллипсы

ìz = h,

Z

ï

Û

í x2

+

y2

=

1 +

z2

ï

îa2

b2

c2

ìz = h,

h

O b

Y

ï

2

y2

a

ï

x

+

Û í

æ

h2

ö

æ

h2

ö

= 1.

ïa2

b2

X

ç1 +

c2

÷

ç1 +

c2

÷

ï

ç

÷

ç

÷

Ðèñ. 5.5

î

è

ø

è

ø

Строим поверхность (рис.5.5).

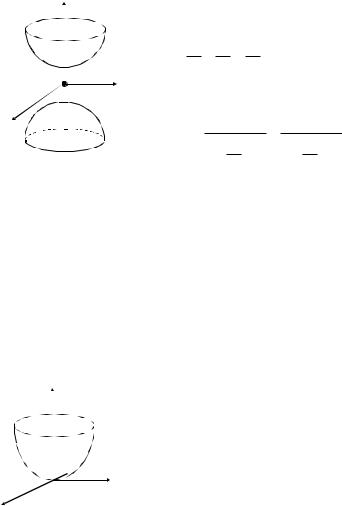
5.4.2. Двухполостный гиперболоид

Поверхность, определяемая уравнением x2 + y2 - z2 = -1. a2 b2 c2

ìïx = 0,

В сечении плоскостью x = 0 — гипербола íz2 - y2 = 1;

ïîc2 b2

&

	Z	в сечении z = h (|h| > c) — эллипсы
		ìz = h,
		ï	+ y2 = h2				Û
		ïí x2			-1
ñ	O	îa2	b2	c2
-ñ		Y
		ìz = h,
		ï	x2				y2
X		ï				+			= 1.
		Û í	æ h2		ö		æ h2	ö
		ïa2 ç		-1÷			b2 ç	-1÷
		ï	ç c2		÷		ç c2	÷
Ðèñ. 5.6		î	è		ø		è	ø
		Получаем поверхность (рис.5.6).

5.5.Параболоиды

5.5.1.Эллиптический параболоид

Поверхность, определяемая уравнением

x2

+

y2

= 2z,

p, q —

p

q

одного знака.

ìx = 0,

x

ï

В сечении плоскостью

=

0 имеем параболу

í

ïy2 = 2qz.

Z

î

В сечении z = h — эллипсы

ìz = h,

ï

x

2

y

2

ãäå h > 0 ïðè p > 0, q > 0;

í

+

= 1,

h < 0 ïðè p < 0, q < 0.

ï

2ph

2qh

î

Y

При p > 0, q > 0 поверхность имеет вид,

O

указанный на рис. 5.7.

X

Ðèñ. 5.7

5.5.2. Гиперболический параболоид

Поверхность, определяемая уравнением	x2	-	y	2	= 2z,	p, q —
одного знака.	p		q

&

ìïy = 0,

В сечении плоскостью y = 0 имеем параболу íïîx2 = 2pz;

сечения плоскостями x = h — параболы:

ì		=		,			ìx = h,
ï	x			h
							ï	æ z -		ö
í y2				=	h2	z	Û íy2 = -2q		h2		;
ï							ï	ç	÷
î q					p		î	è	2p ø

плоскостями z = h (h ¹ 0) — гиперболы:

ìz = h,					ìz		= h,
ï			y2		ï				y2
í x2					Û í x2
ï		-		= 2h,	ï			-		= 1.
î p			q		î	2ph			2qh

Построим гиперболический параболоид для случая p, q > 0 (рис. 5.8). Отметим, что гиперболический параболоид можно рассматривать как поверхность, образованную движением параболы в плоскости x = h при изменении h так, что ее вершина движется по параболе в плоскости y = 0.

Z

Y

O X

Ðèñ. 5.8

Литература: [5. С. 72–83]; [6. С. 104–143; 159–163]; [7. С. 96–106].

&!

Глава 2

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

6. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

Опорный конспект ¹ 6

6.1.Элементы теории множеств

A È B = {x: x Î A Ú x Î B} A Ç B = {x: x Î A Ù x Î B} A\B = {x: x Î A Ù x Ï B} B Ì A Þ A\B = B

6.2.Функции

y = f (x), x Î X, y Î Y Û X ®& Y: " x О X $! y О Y, X = D(f ) — область определения, Y = E(f )&— область значений, x — независимая переменная (аргумент), y — зависимая переменная (функция), R =(-¥, +¥)

6.3. Основные элементарные функции. Элементарные функции

1)

Y

c

O	Õ

1)y = c, c — const

2)y = xn, n О R\{0} — cтепенная, E(f ) зависит от n

3)y = ax, a > 0, a ¹1 — показательная, D(f ) = (-¥, +¥), E(f ) = (0, +¥)

&"

3)		Y	a >1				4)
							Y		à >1
				a <1					X
		O		X			O	1	à <1
5)		Y					Y
		O			X		O		X
						-p -p/2
p	-p/2		p/2	p				p/2	p
		Y					Y
		O		X			O		X
						-p
-p/2							-p/2	p/2	p
				p/2

4)y = loga x, a > 0, a ¹1 — логарифмическая, D(f ) = (0, +¥), E(f ) = (-¥, +¥)

5)Тригонометрические:

y= sin x, D(f ) = (-¥, +¥), E(f ) = [-1, +1]

y= cos x, D(f ) = (-¥, +¥), E(f ) = [-1, +1]

y= tg x, D(f ) = R\{p/2 + kp}, k = 0, ±1, ±2, ..., E(f ) = (-¥, +¥)

y= ctg x, D(f ) = R\{kp}, k = 0, ±1, ±2, ..., E(f ) = (-¥, +¥)

6)Обратные тригонометрические:

y= arcsin x, D(f ) = [-1, +1], гл. значение y О [-p/2, p/2]

y= arccos x, D(f ) = [-1, +1], гл. значение y О [0, p]

6)

Y

Y

p/2

p

O

X

p/2

-1

1

O

-p/2

X

-1

1

Y		Y
		p
p/2
O	X	p/2
-p/2		X
		O

y= arctg x, D(f ) = (-¥, +¥), гл. значение y О (-p/2, p/2)

y= arcñtg x, D(f ) = (-¥, +¥), гл. значение y О (0, p) Сложная функция (суперпозиция функций) y = j[y(x)] Ы

Û y = j(z), z = y(x), x Î X, z Î Z, y ÎY.

Элементарные функции (э.ф.) — записанные одной формулой, составленной из основных э.ф. с помощью символов (+), (-), (´), (:) и операции суперпозиции

6.1. Элементы теории множеств. Символика математической логики.

Топология числовой прямой

Понятие множества, совокупности объектов, элементов является первоначальным, неопределяемым. Например, Х — множество студентов данной аудитории, N = {1, 2, 3, ...} — множество натуральных чисел. Будем обозначать множества заглавными буквами X, Y, A, B; их элементы — строчными x, y, a, b; x О X означает, что элемент х принадлежит множеству Х, х П Х — не принадлежит; А М В — множество А состоит из части элементов множества В, т.е. является подмножеством В.

Множества А и В называют равными, если А М В и В М А.

О: Объединением А И В множеств А и В называется множество, состоящее из элементов, входящих или в А, или в В; пересечением А З В называется множество, состоящее из элементов, входящих в А и в В; разностью А\В множеств А и В называется подмножество множества А элементов, не входящих в В. Если В М А, то В = А\В называется дополнением множества В до множества А.

&$

Примеры:

1){1, 2, 3} È {2, 3, 4} = {1, 2, 3, 4};

2){1, 2, 3} Ç {2, 3, 4} = {2, 3};

3){1, 2, 3} \ {2, 3, 4} = {1};

4){2, 3, 4} Ì {1, 2, 3, 4} Þ {1} = {2, 3, 4}

Пустое множество (множество, не содержащее ни одного элемента) обозначается символом Ж.

n

Åñëè A= U Ak è Àk Ç Àj = Ж (такие множества называются дизъ-

k=1

юнктивными), то для их объединения применяется обозначение

n

A1 + A2 + ... + An = å Ak .

k =1

Подмножества любого множества А с введенными операциями И, З,\ образуют своеобразный математический объект — алгебру множеств, называемую б у л е в о й а л г е б р о й .

Считают, что между множествами Х и Y установлено соответствие (обозначение X ®& Y ), если для любого x О X указаны со-

ответствующие ему О & . y Y

О: Соответствие между X и Y называется взаимно однознач- ным, если для любого x О X существует единственный элемент y О Y и наоборот, для любого y О Y существует един-

ственный элемент x О X (обозначение X «& Y ).

&

О: Два множества X и Y называются эквивалентными, или имеющими одинаковую мощность (X ~Y), если между ними можно установить взаимно однозначное соответствие.

Множество, эквивалентное множеству натуральных чисел N, называется счетным.

Для сокращения записи математических высказываний употребляется символика математической логики. Пусть a, b — некоторые высказывания, относительно которых можно сказать, истинны они или ложны.

Запись a означает «не a«, т.е. отрицание a;

a Ю b — «из a следует b» (Ю — символ импликации);

aЫ b — «a эквивалентно b» (Ы — символ эквивалентности);

aЩ b — «a и b« (Щ — символ конъюнкции);

aЪ b — «a или b« (Ъ — символ дизъюнкции);

"x О A — «для любого x О A» (" — квантор всеобщности);

&%

$y О B — «существует y О B» ($ — квантор существования);

"x О A: a — «для любого х из А имеет место a»;

$! x О Х — «существует единственный х из Х».

Запишем эквивалентность X и Y, используя логическую символику:

X ~ Y Û " x Î Õ $! y Î Y Ù " y Î Y $! x Î Õ.

В дальнейшем в основном рассматривается множество действительных чисел R, состоящее из рациональных и иррациональных чисел, и его подмножества.

Действительные числа изображаются точками числовой оси ОХ. т.е. прямой, на которой выбраны начальная точка О, положительное направление и единица масштаба. К множеству действительных чисел присоединяют два символа -¥, +¥

Î	X	со свойством: " õ Î R Þ -¥ < x < +¥.

Таким образом, R = (-¥, +¥). Интервалы (a, b) = {x: a < x < b}, промежутки [a, b] = {x: a £ x £ b},

(a, b], [a, b) и их объединения являются подмножествами множества R.

О: d — окрестностью U (a) точки а О R называется интервал

d Ú

(а - d, а + d), d > 0, d О R. Проколотой d-окрестностью Ud(a) называется множество Ud(a)\{a}.

О: Точка а О А называется внутренней точкой множества А, если $d > 0: Ud(a) М А. Множество А называется открытым, если оно состоит из внутренних точек.

Пустое множество Ж — открытое множество.

Объединение и пересечение конечного числа открытых множеств — открытые множества.

О: Множество всех открытых множеств числовой оси называется топологией числовой прямой.

6.2. Функции. Область определения. Способы задания

О: Функцией y = f (x), определенной на множестве Х и принимающей значения на множестве Y, называется такое соответствие между этими множествами, при котором для каждого x О Х существует единственный элемент y О Y :

y = f (x), xÎÕ, y Î Y Û X ®& Y: "x Î Õ $!y Î Y.

&

&&

Множество X = D(f ) — область определения функции; Y = E(f ) — область значений функции; х — независимая переменная (аргумент); y — зависимая переменная (функция).

На языке геометрии функция f отображает множество Х на мно-

f

жество Y: X ¾¾®Y , тогда y — образ х, х — прообраз y.

Пример: Функция y = x2, x Î R, y Î [0,+ ¥).

Если каждому значению x О X соответствует несколько или бесконечно много значений y О Y, то считают, что задана многознач- ная функция. При исследовании таких функций выбирают промежутки, где они однозначны. Наиболее часто встречаются три способа задания функции: аналитический, графический, табличный.

При а н а л и т и ч е с к о м способе функция задается одной или несколькими формулами, действующими на непересекающихся частях области определения.

При г р а ф и ч е с к о м способе функция задается кривой (графиком) в плоскости XОY, причем любая прямая, параллель-

ная оси OY, пересекает кривую не более

Y

чем в одной точке. Если функция задана аналитически, то

ее график можно построить. Например,

ì x, x < 0,

ï

функция y = í 2 имеет график, изо-

ïx , x ³ 0

î

браженный на рис.6.1.

При т а б л и ч н о м способе задания имеется таблица значений аргумента и соответствующих значений функции.

X O

Ðèñ. 6.1

Ðèñ. 6.1

О: Функция y = f (x) называется возрастающей на [a, b], если большему значению аргумента соответствует большее зна-

чение функции: x1< x2, x1, x2 Î [a, b] Þ f (x1) < f (x2); убывающей на [a, b], если x1 < x2, x1, x2 Î [a, b] Þ f (x1) > f (x2). Функция только возрастающая или убывающая на [a, b] на-

зывается монотонной.

Например, y = x2 возрастает на [0, +¥) и убывает на (-¥, 0].

О: Функция y = f (x), x О[-a, a], называется четной, если f (-x) = f (x),

нечетной при f (-x) = -f (x)"x.

&'

Например, y = x2 — четная, y = x3 — нечетная функции.

О: Функция y = f (x), x О (-¥, +¥), называется периодической с периодом Т > 0, если f (x + T) = f (x)"x.

Например, y = sin x — периодическая с периодом 2p.

О: Функция x = f -1(y) называется обратной к функции y = f (x), устанавливающей взаимно однозначное соответствие между X = D(f ) и Y = E(f ) (X ¬¾®f Y ), åñëè x = f -1(y) выражает то же соответствие, причем Y = D(f -1), X = E(f -1) ·

Например, x = y обратная к y2 = x ïðè õ Î [0, +¥), y Î [0, +¥).

6.3. Основные элементарные функции. Элементарные функции

К основным элементарным функциям относятся:

1)постоянная y = c, c = const О R;

2)степенная y = xn, n О R \{0}, n задано;

3)показательная y = ax, a > 0, a ¹ 1;

4)логарифмическая y = logax, a > 0, a ¹ 1, x > 0;

5)тригонометрические y = sin x, y = cos x, y = tg x, y = ctg x;

6) обратные тригонометрические y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Области определения, значения этих функий и их графики приведены в опорном конспекте ¹ 6.

Отметим только, что обратные тригонометрические функции являются многозначными (бесконечно значными), при действиях с ними берутся их так называемые главные значения, заклю- ченные в указанных в опорном конспекте ¹ 6 интервалах.

О: Сложной функцией y = j[y(x)] ( или суперпозицией) называется такая функция, для которой y = j(z), y О Y, z О Z, z = j(x), x О X, z О Z Ю y = (j y)x.

Например, y = z2, z = sin x Û y = sin2x.

Пользуясь понятием сложной функции, дадим определение элементарной функции.

'