110
Таблица 13.1 (продолжение)
Диффузия
m~ S ,
m – масса, переносимая через площадку S;
m~Δt ,
t – время;
m~  gradρ
gradρ ;
;
m D ρz S t
– закон Фика.
Знак «–» означает, что перенос массы происходит в сторону уменьшения плотности (концентрации).
D – коэффициент диффузии;
D1  v
v
 λ
λ
3
|
Теплопроводность |
|
Вязкость |
|
(внутреннее трение) |
|
|
|
|
|
|
|
|
|
Q ~ S |
, |
|
|
|
|
|
|
|
|
|
Q – энергия, переноси- |
fx – модуль силы, |
с которой |
|
мая через площадку S; |
один слой площадью S дей- |
|
|
|
|
|
|
|
|
|
Q ~ |
t |
, |
|
ствует на другой; |
|
|
|
|
Q ~ gradT ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
f |
|
η |
u |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q æ |
z |
|
S t |
|
x |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– закон Фурье. |
|
|
|
– закон Ньютона. |
|
|
|
Знак «–» означает, что по- |
|
|
|
|
|
|
|
|
ток тепла идёт в сторону |
|
|
|
|
|
|
|
|
уменьшения |
температу- |
|
|
|
|
|
|
|
|
ры. |
|
|
|
|
|
|
|
|
|
|
|
æ – коэффициент теп- |
|
|
|
лопроводности; |
|
|
η – коэффициент вязкости; |
|
æ |
Вт |
|
|
η Па с . |
|
|
|
м К |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
Для идеального газа: |
|
|
|
æ |
1 |
c ρ v |
λ |
|
η |
1 |
ρ v λ |
|
|
|
|
3 |
V |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Численная оценка
1 5 8,31 103 8 10 7
æ3 2 2,8 10 2
η1 103 2 10 7 7 10 5 Па с 3
Демонстрации: 1) Теплопроводность твёрдых тел 2) Внутреннее трение в газах
111
Лекция 14
2.9.3. Молекулярно-кинетическая теория явлений переноса (на примере внутреннего трения)
Рассмотрим два слоя газа, расстояние меж-
ду которыми равно 2 λ |
, движущихся па- |
раллельно друг другу со скоростями u1 |
и u2 |
u1 ,u2 |
v (РИС. 14.1). |
|
|
В среднем последнее столкновение молеку-
лы происходит на расстоянии λ |
. |
Поэтому |
мы берём u1 u z λ , u2 u z |
λ |
. |
Благодаря тепловому движению молекулы переходят из одного слоя в другой, соударяются друг с другом и обмениваются им-
пульсами (см. «АБСОЛЮТНО УПРУГИЙ УДАР»), в
т. ч. компонентами импульса, соответствующими упорядоченному движению, поэтому ния слоёв выравниваются.
Потери импульса слоя 1 за время t
z
S
z
x
Рис. 14.1
импульсы упорядоченного движе-
где m0 – масса молекулы, N12 – число молекул, перешедших из слоя 1 в слой 2; импульс, приобретённый слоем 1,
где N21 – число молекул, перешедших из слоя 2 в слой 1. Изменение импульса слоя 1
(ср. 2.2.3), n – концентрация газа,
p1
так как m0n = ρ – плотность газа,
так как N = const. Изменение импульса слоя 1
|
|
m n |
S |
v u2 u1 ; |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
p |
|
|
1 |
S |
v ρ u2 u1 ; |
|
1 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
6 |
|
|
|
|
u2 |
u1 |
u |
z , |
|
z |
|
|
|
|
|
|
|
|
|
По закону Ньютона |
fx η |
u |
S |
|
z |
|
|
|
|
1. Механика37
 .
.
1.11. Принцип относительности Галилея. Преобразования Галилея
Принцип относительности Галилея: все инерциальные системы отсчёта эквивалентны. Никакими опытами, поставленными внутри ИСО, нельзя определить, движется ли она или покоится.
1.11.1. Преобразования Галилея
Пусть имеются две инерциальные системы отсчёта K и K′. Система K′ движется относи-
тельно системы K со скоростью v (РИС. 14.2).
Зная координаты и время в системе отсчёта K, найдём координаты и время в системе K′ и наоборот, т. е. найдём связь между x, y, z, t и x′, y′, z′, t′ (ТАБЛ. 14.1).
В классической механике время во всех системах отсчёта течёт одинаково.
Рис. 14.2 |
|
Таблица 14.1 |
|
Преобразования Галилея |
|
|
|
K′ → K |
|
K → K′ |
x x vt |
|
x x vt |
y y |
|
y y |
z z |
|
z z |
t t |
|
t t |
1.11.2. Следствия из преобразований Галилея
Инвариант преобразований – физическая величина, которая не изменяется при переходе из одной системы отсчёта к другой, т. е. величина, значения которой одинаковы во всех системах отсчёта.
1. Абсолютность одновременности
События, одновременные в одной системе отсчёта, одновременны и в другой. Это следует из того, что время является инвариантом преобразований Галилея:
37 Параграфы 1.11-1.14 выносятся на конец I семестра.
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Инвариантность длины отрезка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
y′ |
|
|
|
|
Пусть отрезок |
|
1-2 |
покоится относи- |
|
t |
|
t′ |
|
|
тельно системы отсчёта K′ |
|
(РИС. 14.3). |
|
|
|
|
2 |
|
|
|
|
|
l′ |
|
|
|
|
|
|
|
Его длина в этой системе отсчёта равна |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l′. Выразим l′ через координаты концов |
|
|
|
|
|
|
отрезка в системе K′: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
x2 |
x1 |
y2 y1 |
|
|
|
|
K′ |
|
|
Свяжем координаты концов стержня в |
|
|
|
O′ |
|
|
|
x′ |
|
K |
|
|
|
системе отсчёта K′ |
с координатами в |
|
|
|
|
|
|
системе отсчёта K через преобразова- |
|
|
|
|
|
|
|
|
O |
|
|
|
|
x1 |
x2 |
x |
ния Галилея: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l x |
|
vt x |
|
|
|
2 |
y |
|
2 |
|
|
|
|
Рис. 14.3 |
|
|
2 |
1 |
vt |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
2 |
|
y |
2 |
l |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
– длина отрезка в системе отсчёта K. Это означает, что длина отрезка – инвариант преобразований Галилея:
l l inv .
3. Инвариантность интервала времени
Пусть интервал времени между двумя событиями 1 и 2 в системе отсчёта K′
Интервал времени между теми же событиями в системе отсчёта K
4. Классический закон сложения скоростей
Пусть материальная точка движется со скоростью счёта K′. Тогда её скорость в системе отсчёта K
|
u u v |
. |
|
|
|
|
|
Доказательство |
|
|
|
|
По определению скорости |
|
|
|
|
ux |
dx |
|
dx |
. |
|
|
dt |
, ux |
dt |
|
|
|
Выразим ux через координату и время в системе отсчёта K′:
ux |
dx vdt |
|
dx |
|
|
|
|
dt |
|
|
|
dt |
v ux v . |
|
|
|
|
|
|
|
|
|
Аналогично получим |
|
|
|
|
|
|
|
|
|
|
|
u |
y |
dy , u |
dy u |
y |
u |
; |
|
dt |
y |
|
dt |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
u u |
. |
|
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
114
5. Инвариантность ускорения
По определению, ускорение материальной точки в системе отсчёта K′
|
|
|
|
|
|
du |
, |
a |
dt |
|
|
|
|
|
в системе отсчёта K |
|
|
|
|
a |
du |
|
dt |
|
|
|
|
(здесь мы используем те же обозначения, что в ПРЕДЫДУЩЕМ ПОДРАЗДЕЛЕ). Воспользуемся классическим законом сложения скоростей:
|
|
|
|
d u v |
|
du |
a ; |
|
|
|
|
u |
u v , a |
dt |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a a inv |
. |
|
|
|
|
|
|
|
|
|
|
|
6. Инвариантность массы и силы
Постулируется, что масса и сила – инварианты преобразований Галилея:
|
|
|
F F inv |
|
|
m m inv |
, |
. |
|
|
|
|
|
II закон Ньютона инвариантен относительно преобразований Галилея: |
|
F |
|
|
F ma . |
|
|
|
ma |
|
1.12. Специальная теория относительности
1.12.1. 4-пространство
Время относительно, как и пространство. Введём 4-пространство – линейное риманово (неевклидово) пространство координат и времени.
4-радиус-вектор:
здесь c – константа, имеющая размерность скорости; i – мнимая единица. Модуль 4-радиуса-вектора
r 
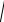 x2 y2 z2 c2t2 inv
x2 y2 z2 c2t2 inv
(доказательство см. «ИНВАРИАНТНОСТЬ ИНТЕРВАЛА»).
Мировая точка – точка в 4-пространстве. Мировая линия – кривая в 4-пространстве.
ПРИМЕР
Материальная точка покоится в 4-пространстве. Мировая линия – траектория этой материальной точки в 4-пространстве (вернее, двумерная её проекция) – изображена на РИС. 14.4.
115
x
Рис. 14.4
1.12.2. Преобразования Лоренца
II закон Ньютона инвариантен относительно преобразований Галилея, а уравнения Максвелла (см. 3.1.6) – нет. Надо получить другие преобразования, опираясь на свойства симметрии пространства-времени38 (см. 1.1.2).
Пусть имеются две инерциальные системы отсчёта K и K′. Система K′ движется
относительно системы K со скоростью v (РИС. 14.2). В момент совмещения начал координат часы синхронизированы: x = x′ = y = y′ = z = z′, t = t′.
Искомые преобразования должны иметь вид
x f x
t g x,
где f и g – функции, которые нужно найти.
При сдвиге координаты в системе отсчёта щие сдвиги в системе K′
,t,v , t ,v ,
K на x и времени на t соответствую-
|
x |
|
f x x,t t,v f x,t ,v , |
|
|
|
t g x x,t t,v g x,t ,v . |
|
|
|
|
|
Это возможно только тогда, когда f и g – линейные функции x и t:
x a x a vt , |
|
1 |
2 |
a |
|
|
x a t. |
t |
3 |
|
v |
4 |
|
|
Коэффициенты a1, a2, a3, a4 безразмерны. Их можно найти с помощью элементарных преобразований. В результате получаются преобразования Лоренца, приведённые в ТАБЛИЦЕ 14.2.
38 Упрощённый вывод (для двумерного пространства-времени x, t) приведён в ПРИЛОЖЕНИИ. Делать его на лекции не рекомендуется из-за громоздкости элементарных алгебраических преобразований.
116
Таблица 14.2
Преобразования Лоренца
K → K′
x |
x vt |
|
|
|
|
|
|
2 |
|
|
1 |
|
v |
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y |
|
|
|
|
|
z z |
|
|
|
|
|
|
|
t |
v |
|
x |
t |
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
v |
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь c = const. Видно, что v < c, т. е. c – предельная скорость. Из опыта известно, что c – скорость света в вакууме.
При v << c преобразования Лоренца переходят в преобразования Галилея.
Подчеркнём, что преобразования Лоренца выводятся из свойств симметрии про- странства-времени и не требуют других допущений. Однако, во многих учебниках (например, [1]) преобразования Лоренца выводятся другим способом – через постулаты Эйнштейна.
Постулаты Эйнштейна
1.ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
2.Скорость распространения взаимодействий инвариантна относительно преобразований.
117
Лекция 15
1.12.3. Следствия из преобразований Лоренца
1. Инвариантность интервала
Интервал между событиями 1 и 2
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
S |
c |
t |
|
t |
|
|
x |
|
x |
|
|
y |
y |
|
z |
z |
|
. |
12 |
|
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
2 |
1 |
|
Интервал – инвариант преобразований Лоренца:
S12 inv .
Доказательство
Докажем, что малый интервал – дифференциал интервала dS12 образований Лоренца:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
dx |
2 |
dy |
2 |
dz |
2 |
2 |
2 |
2 |
dx |
2 |
dy |
|
2 |
|
|
dS12 |
c dt |
|
|
|
|
, dS12 |
c dt |
|
|
|
|
|
через время и координаты в системе отсчёта K: |
|
|
|
Выразим dS12 |
|
|
|
|
|
2 2 |
|
|
v2 |
2 |
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c dt |
|
|
|
|
dx |
|
2vdxdt dx |
|
v dt |
|
2vdxdt |
dy2 dz2 |
|
|
dS 2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
1 |
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 v2 dt2 |
v |
1 |
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
2 |
|
|
|
2 |
2 2 |
|
2 |
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
dz |
|
c dt |
|
dx |
|
dy |
|
dz |
|
dS12 |
, |
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч. т. д.
2. Сокращение длины движущегося отрезка (лоренцево сокращение)
l0
1 2
2
|
K′ |
|
|
|
O′ |
|
x′ |
|
K |
|
|
O |
x1 |
x2 |
x |
|
|
|
|
Рис. 15.1 |
|
|
Пусть отрезок 1-2 покоится относительно системы отсчёта K′; для простоты расположим его вдоль оси x′ (РИС. 15.1). Длина отрезка в системе отсчёта, в которой он покоится, – соб-
ственная длина отрезка l0 l .
Выразим длину отрезка в системах отсчёта K′ и K через координаты его концов:
l x x ,
0 2 1
l x2 x1.
Выразим l0 через координаты и время в системе отсчёта K:
l |
|
x |
2 |
vt |
|
x |
1 |
vt |
|
x |
2 |
x |
1 |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
v |
2 |
|
|
|
|
v |
2 |
|
|
|
|
v |
2 |
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
c |
2 |
|
c |
2 |
|
c |
2 |
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
время t в обоих слагаемых этой формулы одно и то же, так как измерение координат x1 и x2 проводится одновременно. Получается, что
l < l0 – длина движущегося отрезка меньше длины покоящегося.
3. Замедление хода движущихся часов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
y′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеются часы с пружинным (или дру- |
|
t |
|
t′ |
|
|
|
|
|
|
|
|
|
|
|
гим) маятником, покоящиеся относи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельно системы отсчёта K′ (РИС. 15.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Период колебаний маятника в системе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсчёта, |
относительно которой |
точка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подвеса маятника покоится ( x1 x2 ), – |
|
|
|
|
K′ |
|
|
|
|
|
|
|
|
период собственных колебаний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T0 T |
|
, |
|
|
|
|
O′ |
|
|
|
|
|
|
|
|
|
x′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
T t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[события 1 и 2 – два последо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
вательных прохождения маятником |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положения равновесия (или любой |
|
|
|
|
Рис. 15.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
другой фазы колебаний]. В системе от- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
счёта K события 1 и 2 происходят в |
точках с разными координатами x1 и x2, период колебаний маятника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T t2 t1 . |
|
|
|
|
|
|
|
|
|
|
Выразим эту величину через координаты и время в системе отсчёта K′: |
|
|
|
|
|
|
|
|
|
|
t |
|
v |
x |
|
t |
|
v |
x |
|
|
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
2 |
|
c |
2 |
2 |
|
1 |
|
c |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
v |
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
c |
2 |
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T > T0 – ход движущихся часов замедляется. |
|
|
|
|
4. Относительность одновременности |
|
|
|
|
|
Если события 1 и 2 в системе отсчёта K′ происходят в одно и то же время (t |
t ), |
|
|
|
|
|
|
|
|
2 |
1 |
но в разных местах ( x |
x ), то t2 ≠ t1 – эти события не одновременны в системе |
|
|
|
2 |
1 |
|
|
|
|
|
|
отсчёта K. Это следует из преобразований Лоренца. |
|
При t |
t |
и x |
x возможно t2 < t1. Однако, если между событиями 1 и 2 имеется |
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
причинно-следственная связь, то она не нарушается и t2 > t1.
5. Релятивистский закон сложения скоростей
Пусть материальная точка M движется
со скоростью u относительно системы отсчёта K′ (РИС. 15.3). Найдём её скорость в системе отсчёта K.
По определению, проекции скорости в системе отсчёта K′
Рис. 15.3
наты и скорости в системе отсчёта K′:
|
dx |
|
dy |
|
dz |
; |
|
|
|
ux |
dt |
, uy |
dt |
, uz |
dt |
|
|
|
|
в системе отсчёта K
|
ux |
dx |
, uy |
dy |
, uz |
dz |
. |
|
dt |
dt |
dt |
|
|
|
|
|
Выразим эти проекции через коорди-
|
|
|
|
|
|
dx vdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
v |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
, dy dy , |
dz dz , |
dt |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
1 |
|
|
|
|
u |
1 |
|
|
|
|
|
u |
1 |
|
|
dx vdt |
|
u |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
y |
|
|
|
c |
2 |
|
|
|
|
z |
|
|
|
c |
2 |
|
|
|
|
|
x |
|
|
|
, uy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, uz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
v |
dx |
|
1 |
|
v |
u |
|
|
|
dt |
v |
dx |
|
1 |
v |
u |
|
|
|
|
|
1 |
v |
u |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
c |
|
|
|
|
c |
x |
|
|
|
|
|
c |
|
|
|
|
|
|
|
c |
|
x |
|
|
|
|
|
c |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
1 |
v2 |
|
|
|
u |
|
|
1 v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
c |
2 |
|
|
, u |
z |
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
u |
x |
|
|
|
|
, u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
v u |
|
|
|
|
|
v |
u |
|
|
|
|
|
z |
|
|
|
v u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
x |
|
|
|
|
c2 |
x |
|
|
|
|
|
|
|
|
c2 |
|
x |
|
|
|
|
|
|
Ускорение не является инвариантом преобразований Лоренца. Формулы для преобразования компонент ускорений можно получить аналогичным образом – исходя из определения и преобразований Лоренца:
1.13. Релятивистская динамика
1.13.1. Релятивистский импульс
Рассмотрим замкнутую механическую систему – два груза одинаковой массы m0, соединённых пружиной (РИС. 15.4). В системе отсчёта K′ центр масс данной механической системы покоится. В начальном состоянии пружина сжата, затем она
разжимается и грузы движутся со скоростями
Должен выполняться закон сохранения импульса: импульс данной замкнутой механической системы должен сохраняться в любой инерциальной системе отсчёта.







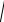 x2 y2 z2 c2t2 inv
x2 y2 z2 c2t2 inv





 grad
grad ;
; v
v
 λ
λ
 λ
λ
 v
v 1 10
1 10 v
v
 λ
λ

 S
S  v
v
 λ
λ .
. 2
2