Конспект лекций по общей физики (1-4 семестр)

70

Лекция 8

2. Молекулярная физика и термодинамика

2.1. Предмет термодинамики и статистической физики. Молекулярно-кинетическая теория. Уравнение состояния

2.1.1. Постулаты молекулярно-кинетической теории (МКТ)

1.Все тела состоят из мельчайших частиц (молекул).

2.Эти частицы находятся в непрерывном хаотическом (тепловом) движении и взаимодействии.

ПРИМЕРЫ

1. Броуновское движение
Броуновское движение – движение частиц, взвешенных в
жидкости или газе. Под микроскопом видно, что частицы
дрожат.
Это явление объясняется тем, что взвешенная частица (боль-
шое пятно неправильной формы на РИС. 8.1) испытывает бес-
порядочные столкновения с молекулами жидкости или газа
(изображены на РИС. 8.1 мелкими кружками), которые в мик-		Рис. 8.1
роскоп не видны. В результате этих столкновений взвешен-
ной частице передаётся импульс	p ; эта величина изменяет-

ся непрерывно и хаотически – частица дрожит. Демонстрация: Модель броуновского движения

2. Явления переноса

Кинетические явления – диффузия, теплопроводность и внутреннее трение - объясняются только из молекулярно-кинетических представлений (см. РАЗДЕЛ 2.9.3).

Взаимодействие молекул носит характер притяжения и отталкивания, в зависимости от расстояния между молекулами. График зависимости потенциальной энергии Wп взаимодействия двух молекул от расстояния r между их центрами представлен на РИС. 8.2. «Радиус молекулы» r0 ≈ 10–10 м.

Демонстрация: Сцепление свинцовых цилиндров

Количество вещества – мера числа частиц;

[ν] = моль.

В 1 моле содержится NA = 6,02·1023 (моль–1) ча-

стиц – число Авогадро;

Wп

отталкивание

0	r0	r

притяжение

Рис. 8.2

масса молекулы

71

	ν	N
		N
		A

где N – число молекул.

Молярная масса – масса 1 моля вещества;

,

	μ			кг
			моль
		μ		m	,
				ν

;

где m – масса вещества. Молярную массу легко вычислить по таблице Менделеева, зная химическую формулу вещества:

μ

1 атомная единица массы (а. е. м.) m1

3	m	кг ;
	0
10	m
	1

а. е. м.

= 1,6606·10–27 кг.

2.1.2. Микропараметры и макропараметры. Статистический и термодинамический методы исследования макросистем

Термодинамическая система (макросистема) – совокупность (коллектив)

большого числа частиц.

Пусть термодинамическая система состоит из N частиц. Микросостояние системы характеризуется 6N микропараметров – 3 координатами и 3 проекциями скорости каждой частицы (xi, yi, zi; vxi, vyi, vzi). Эти параметры можно найти, решив систему из N дифференциальных уравнений движения материальной точки, задав начальные условия – 6N параметров. Это практически невозможно из-за большого числа параметров. Более того, термодинамическая система является стохастической, т. е. её движение неустойчиво по отношению к изменению начальных условий. Поэтому разработаны методы описания состояния системы без решения уравнений динамики.

Термодинамические параметры – параметры, описывающие термодинамическую систему в целом: p, T, S, V, U28 и т. д. (Так, температура T – это мера нагретости тела.)

Макросостояние системы характеризуется совокупностью термодинамических параметров.

Методы исследования термодинамических систем

термодинамический	статистический
основан на общефизических за-	использует модельный подход
конах	Исходя из модели, находят тер-
	модинамические параметры.

28 Каждое из этих обозначений разъяснено далее в тексте данной главы.

72

2.1.3. Термодинамический процесс. Уравнение состояния

Термодинамический процесс – изменение макросостояния термодинамической системы.

Равновесное состояние (состояние термодинамического равновесия) – макро-

состояние, которое сохраняется сколь угодно долго при неизменных внешних условиях. Имеет смысл вводить термодинамические параметры только для равновесных состояний.

Равновесный процесс – термодинамический процесс, при котором система проходит через ряд последовательных равновесных состояний. Равновесный процесс должен быть квазистатическим – протекать бесконечно медленно.

Уравнение состояния – уравнение, связывающее термодинамические параметры системы (как правило, давление p, объём V и температуру T):

f p,V ,T const

.

Такое уравнение можно аналитически точно записать только для одной термодинамической системы – идеального газа.

2.2. Идеальный газ

2.2.1. Модель идеального газа

Идеальный газ – коллектив огромного числа молекул:

1.Расстояние между молекулами много больше их линейных размеров29 и собственным объёмом молекул можно пренебречь по сравнению с объёмом, занимаемым газом.

2.Молекулы находятся в непрерывном хаотическом движении.

3.Молекулы взаимодействуют между собой и со стенками сосуда посредством абсолютно упругого удара. Между соударениями молекулы не взаимодействуют.

На РИС. 8.3 показано, как модель идеального газа аппроксимирует экспериментальную зависимость потенциальной энергии взаимодействия двух молекул от расстояния между их центрами (РИС. 8.2).

Wп

Модель идеального газа

0	r0	r

Экспериментальная зависимость

Рис. 8.3

29 Хотя размеры молекул малы, молекулы сталкиваются друг с другом. Можно показать это путём численной оценки.

73

2.2.2. Уравнение состояния идеального газа. Газовые законы

Уравнение состояния идеального газа:

pV T

const

.

Это уравнение является обобщением экспериментальных фактов.

Частные случаи (газовые законы):

1.T = const: pV const – закон Бойля-Мариотта

	2.	p = const:	V	const	– закон Гей-Люссака
			T
	3.	V = const:	p	const	– закон Шарля
			T
	Уравнение состояния идеального газа можно представить в виде
						pV	m	RT
							μ
										Дж
	– уравнение Менделеева-Клапейрона, R							8,31			– универсальная газовая
										моль К

постоянная.

Преобразуем уравнение Менделеева-Клапейрона, подставив

					pV νRT	N		RT NkT ,
						N
							A	k
k	R		23	Дж	– постоянная Больцмана.
	N		1,38 10	К
		A

ν

m μ

:

(8.1)

Концентрация – характеристика макросистемы, равная числу частиц в единичном объёме:

	n	N	; [n] = м–3.
		V
Из (8.1) получим
		p N kT ,
			V
		p nkT			(8.2)

– основное уравнение МКТ для давления.

Закон Дальтона: давление смеси газов равно сумме парциальных давлений компонент смеси:

p pi .

Доказательство
Запишем уравнение (8.2) для i-ой компоненты смеси:
pi nikT .	(8.3)
Общая же концентрация смеси

74

			i			i
n	N		N		N		ni	,
	V		V		V

где Ni – число молекул i-ой компоненты. Теперь просуммируем выражения (8.3) по всем компонентам смеси:

pi nikT kT ni nkT ,

что, согласно (8.1), равно давлению p смеси.

Хотя идеальный газ – это модель, газовые законы хорошо работают в условиях, близких к нормальным.

Нормальные условия: p0 = 1,01·105 Па; T0 = 273 К.

2.2.3. Вывод основного уравнения МКТ

Рассмотрим равновесный газ, состоящий из одинаковых молекул массой m0. Все молекулы имеют разные по модулю и направлению скорости. Давление газа обусловлено ударами молекул о стенку сосуда.

1. Удар одной молекулы

m0

x

Рис. 8.4

Пусть молекула массой m0 движется перпендикулярно стенке

со скоростью

v

и испытывает абсолютно упругий удар

(РИС. 8.4). После удара молекула отскакивает со скоростью v

(см. «УДАР ШАРА ОБ УПРУГУЮ ПЛИТУ»). По II закону Ньютона из-

менение импульса молекулы при ударе

m0 v f	τ ,
*

где f * – сила, с которой стенка действует на молекулу, τ –

длительность удара. Спроецируем это равенство на ось x:

m v m v f
0	0

*τ

.

По III закону Ньютона сила, с которой молекула действует на стенку,

f f	*	f

f 2mτ0v .

2. Число ударов о стенку за время t >> τ

f

*

,

m0

S

vi t

x

Рис. 8.5

Рассмотрим i-ю скоростную группу молекул, т. е. молекулы со скоростями v = (vi, vi ± v). Выделим прямой цилиндр, одно из оснований которого площадью S прилегает к стенке сосуда, а высота равна vi t (РИС. 8.5). Число молекул внутри этого цилиндра, которые долетят до стенки за время t,

Ni n6i vi t S ,

где ni – концентрация i-ой скоростной группы; коэффициент 1/6 обусловлен тем, что из всех молекул 1/3 движется вдоль оси x, из них ½ движется в направлении стенки.

75

3. Импульс, полученный стенкой от молекул i-ой скоростной группы за время t

Средний импульс, переданный стенке молекулами i-ой скоростной группы, равен сумме импульсов ударов отдельных молекул этой группы (все выражения далее записываем в проекции на ось x):

		fiτ 2m0vi	Ni 2m0vi	n		t S 2m0vi	m	2
Fi	t			i	vi		0		t S ,
				6			3	ni vi

3

здесь Fi – суммарная сила, с которой молекулы i-ой скоростной группы действуют на стенку. Давление молекул i-ой скоростной группы

									pi					F						m n v							2
																													.
															i						0			i		i
															S							3
4. Учёт давления всех скоростных групп молекул
По закону Дальтона
				p pi							m			ni vi										m					ni vi		n	;
												0															0
																				2										2
											3														3						n
													n ni									;
					n v		2	n v					2						n v					2							n v		2
			2
		v			1	1					2	2									i			i						i			i	;
						n			n									n													n
								1				2								i
											p				m n							2
																	0			v					.
																	3
v	2	vкв – средняя квадратичная скорость молекулы идеального газа.
Преобразуем результат (8.4):
											p			2					m v				2
																n
																				0
														3						2

– основное уравнение МКТ идеального газа;

(8.4)

p2nε

3

(8.5)

– основное уравнение МКТ идеального газа для энергии. Здесь ε – средняя ки-

нетическая энергия молекулы идеального газа (поступательного движения).

2.2.4. Молекулярно-кинетическое толкование абсолютной температуры

Из двух форм основного уравнения МКТ (8.2) и (8.5) следует

p	2	n ε
	3			kT	2	ε
					3
p nkT

Абсолютная температура пропорциональна ступательного движения, приходящейся на 1

		ε	3	kT .
			2

средней кинетической энергии помолекулу.

Энергетическая температура

76

θ kT

2ε

3

2 m0v2

3 2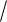

.

Среднеквадратичная скорость молекулы идеального газа

v		2 ε			2 3kT		3kT		3RT	;
кв		m0			2m0		m0		μ

v		3RT
кв		μ

.

Численная оценка

При t = 27°C (T = 300 К) для кислорода (µ = 3,2·10–2 кг/моль):

θ = 4,2·10–21 Дж;

		2				м
v		3 8,31 3 10	2	3	2,6 483
		2	10
кв						с
		3,2 10

.

77

Лекция 9

2.3. I начало термодинамики

2.3.1. Внутренняя энергия

Внутренняя энергия термодинамической системы – это:

1.Кинетическая энергия поступательного и вращательного движения молекул (теплового движения)

2.Потенциальная энергия взаимодействия молекул

3.Потенциальная энергия взаимодействия атомов в молекуле

4.Энергия атомных оболочек

5.Внутриядерная энергия

2.3.2. Внутренняя энергия идеального газа

Внутренняя энергия идеального газа – кинетическая энергия поступательного и вращательного движения молекул.

Для одноатомного газа с учётом того, что средняя кинетическая энергия поступа-

	тельного движения молекулы	ε		3	kT , получим выражение для внутренней
				2

энергии

U N	ε		3	NkT	3	νN	kT	3	νRT	3 m	RT
			2		2	A		2		2 μ

.

Число степеней свободы i механической системы – наименьшее число независимых координат, с помощью которых определяется положение системы в пространстве.

Число степеней свободы молекул указано в ТАБЛИЦЕ 9.1.

Закон равномерного распределения энергии по степеням свободы: в любой термодинамической системы на одну степень свободы молекулы приходится

энергия, в среднем равная

kT 2

.

Доказательство

Для поступательного движения εпоступ 32kT и

		m	v	2
ε		0
поступ			2

m0 v2 v2

2 x y

ε1

v	2
	z

kT

2

m	v	2		m	v	2		m	v
		x				y
0				0				0
	2				2				2

, ч. т. д.

2 z

3ε1

;

Внутренняя энергия идеального газа равна сумме кинетических энергий поступательного и вращательного движения всех молекул газа:

U N

ε

N

i

NkT

i

νN

kT

i

νRT

i

m

RT

2

2

A

2

2 μ

U 2i mμ RT .

,

						78
									Таблица 9.1
Одноатомная молекула				Двухатомная молекула				Многоатомная молекула
z					z	z		z	z
									y
						x			x
O			y		O		y	O	y
x				x				x
i 3						i 5			i 6
3 степени свободы,				3 степени свободы,				3 степени свободы,
соответствующие				соответствующие				соответствующие
поступательному				поступательному				поступательному
движению					движению			движению
				+ 2 степени свободы,				+ 3 степени свободы,
				соответствующие				соответствующие
				вращательному				вращательному
					движению			движению
Внутренняя энергия идеального газа – функция							p
состояния термодинамической системы.
Изменение внутренней энергии при переходе си-								1
стемы из состояния 1 в состояние 2 (см. диаграм-
му РИС. 9.1)
U U2 U1	i	m	R T2	T1	i m				2
						R T .
	2 μ				2 μ
							O		V
Изменение внутренней энергии термодинамиче-
								Рис. 9.1
ской системы не зависит от способа перехода си-
стемы из одного состояния в другое, а определя-
ется только начальным и конечным состояниями системы.

2.3.3. Работа газа

dV

p

Рис. 9.2

Пусть газ находится под подвижным поршнем под давлением p

(РИС. 9.2). Поршень совершает малое перемещение dl , при этом объём газа изменяется на dV. Газ действует на поршень с силой

F , F = pS, где S – площадь поршня. Найдём работу газа δA при элементарном расширении:

δA Fdl Fdl pSdl pdV ,

δA pdV .

Работа газа

79

2 A pdV

1

.

Графический смысл работы – площадь под гра-	p
фиком p(V) (РИС. 9.3).
Работа – характеристика не макросостояния тер-		1
модинамической системы, а термодинамического			2
процесса, она зависит от способа перехода из
начального в конечное состояние. Поэтому эле-
ментарная работа не является полным диффе-
ренциалом какой-либо величины – функции со-	0	V1	V2 V
стояния. По этой причине малое приращения ра-
боты (и других величин, не являющихся полными			Рис. 9.3

дифференциалами) принято обозначать буквой δ, а малое приращение температуры, объёма, внутренней энергии и т. п. – знаком дифференциала d.

ПРИМЕР

Работа при изотермическом расширении идеального газа

Идеальный газ расширяется при постоянной температуре от объёма V1 при давлении p1 до объёма V2. Найти работу газа.

Из уравнения состояния идеального газа:

pV const pV p1V1			,
p V	p1V1	.
	V

График30 этой функции представлен на РИС. 9.4. Вычислим работу:

	V		V		dV		V
	2	p V dV	2
A				p1V1		p1V1 ln	2	.
	V		V		V		V
							1
	1		1

2.3.4. Количество теплоты. Теплоёмкость

p

p1 1

p2		2
0	V1	V2 V
		Рис. 9.4

Количество теплоты – характеристика термодинамического процесса – энергия, передаваемая термодинамической системе без совершения работы.

Теплоёмкость системы (тела) – характеристика термодинамической системы и совершаемого ею процесса, равная количеству теплоты, которое необходимо передать системе для нагревания её на один градус:

C	δQ	; C	Дж .
	dT		К

Удельная теплоёмкость вещества – теплоёмкость вещества единичной массы:

c	δQ	; c	Дж	.
	mdT
			кг К

30 На графиках термодинамических процессов следует обозначать начальное и конечное состояния и направление процесса.