Методические указания к выполнению практических занятий по обработка статистических данных и проверка статистических гипотез

1. Цель работы – выработка практических навыков по обработке статистических данных и проверке статистических гипотез.

2. Основные теоретические положения. При применении статистических методов оценки в практиче­ских условиях очень часто возникает вопрос о проверке исход­ных данных на однородность. Однородность – это свойство, заключающееся в том, что все колебания измеряемых параметров определяются воз­действием случайных факторов, а не какими-либо иными при­чинами. К таким причинам можно отнести, например: различные технологические процессы изготовления испытываемых изделий, различные условия испытаний, ошибки измерений и т.д. В тех случаях, когда известно, что отдельные результаты получены вследствие нару­шения программы испытаний, ошибок измерения и других при­чин, их следует отбросить, не подвергая никаким статистиче­ским оценкам. Когда же имеется лишь подозрение на то, что отдельные результаты являются ошибочными, то исходные ста­тистические данные до последующей обработки подлежат проверке на однородность. При наличии сомнительных результатов применяются два метода проверки на однородность.

Метод 1. Пусть х₁, х₂, ... х_N ( х₁ ≤ х₂ ≤ ... ≤ х_N ) – резуль­таты измерений; x_N+1 – сомнительный результат; N+1 – общее число результатов: β – вероятность ошибки, заключающейся в том, что результат x_N+1 будет признан ошибочным, хотя он является правильным. Однородность результатов прове­ряется следующим образом:

- определяется величина ͞x по формуле

;

- определяется величина t_э по формуле t_Э = /S;

- оценивается результат х_N+1:

если t_э > t₂(β, N+1), то результат х_N+1 отбрасывается,

если t_э ≤ t₂(β, N+1), то результат х_N+1 принимается.

В том случае, если имеются два сомнительных результата – х₁ (x₁<x₂) и х_N+1, то в указанной выше последовательности произво-дится их раздельная оценка. Аналогично производится оценка и в случае наличия нескольких сомнительных ре­зультатов.

Пример 1. Измерения относительной погрешности определе-

ния расстояния с помощью радиолокационной аппаратуры дали сле-

дующие результаты: – 0,05; – 0,04; – 0,03; – 0,02; – 0,01; – 0,01; 0,00; + 0,01; +0,01, +0,02; +0,03; +0,09.

Требуется оценить результат х_N+1 = +0,09 при β = 0,05.

Решение. По первому методу имеем: ͞x = (– (0,05 + 0,04 + + 0,03 + 0,02 + 0,01 + 0,01) + (0 + 0,01 + 0,01 + 0,02 + 0,03 + 0,09)) / 11 = 0 / 11 = 0.

S =2,66 ∙10^-2.

t₁(β, N) = 2,327; Δ= 0,09 – 0 = 0,09; Δ = 0,09 > S∙t₁(β, N) =

= 2,66 ∙10^-2  2,327 = 0,062. Результат х_N+1 = +0,09 должен быть отброшен.

По второму методу имеем: ͞x = 0,09 / 12 = 0,75∙10^-2.

t₂(β, N+1) = 1,46;

; t_э = 1,58 > t₂(β, N+1) = 1,46.

Оценка результата х_N+1 по обоим методам совпадает.

Фрагменты таблиц значений t₁ (β, N) и t₂(β, N+1) приведены в табл.18.

Таблица 18

N	t1 (β, N)			N+1		t2(β, N+1)
	β = 0,05	β = 0,01	β = 0,05			β = 0,01
8	2,508	3,711	8		1,70		2,26
9	2,431	3,536	9		1,60		2,13
10	2,372	3,409	10		1,50		2,00
11	2,327	3,310	11		1,48		1,98
12	2,291	3,233	12		1,46		1,96
13	2,261	3,170	13		1,44		1,94
14	2,236	3,118	14		1,42		1,92

В тех случаях, когда имеются результаты различных серий испытаний (выборок), отличающиеся друг от друга, проверка на однородность обычно производится путем оценки случайно­сти расхождения между двумя выборочными средними (иногда вместо этого метода применяется описываемый ниже метод, основанный на использовании критерия χ² Пирсона) с ис­пользованием критерия t Стьюдента.

Пусть N₁, N₂ – объемы выборок; ͞x₁, ͞x₂, – выборочные средние значения .

Однородность выборок проверяют следующим образом:

- определяются величины S₁^΄2 и S₂^΄2 по формулам:

.

- определяется величина S по формуле

;

- определяется величина Δ по формуле

Δ = │ ͞x₁ – ͞x₂ │;

- определяется величина t по формуле

;

- по известным величинам t и k = N₁+N₂ – 1 в по таблицам определяется величина S(t);

- оценивается случайность расхождения между двумя выбо­рочными средними: если S(t) ≤ 1– β / 2, то расхождение несущественно, если S(t) > 1– β / 2, то расхождение существенно.

Пример 2. Измерения наработки ЭС до отказа дали следую-щие результаты:

Наработка, ч	N	0 - 200	200 - 400	400 - 600	600 - 800	800 - 1200
первая серия	100	40	25	13	10	12
вторая серия	150	64	35	20	13	18

Требуется определить однородность выборок при β = 0,05 и 1– β / 2 = 0,975.

Решение. Отнеся статистические данные к серединам соответствующих интерва­лов, найдем: N₁ = 100; N₂ = 150 и

͞x₁ = 1 / 100 ∙ (40∙100 + 25∙300 + 13∙500 + 10∙700 + 12∙1000) = 370;

͞x₂ = 1 / 150 ∙ (64∙100 + 35∙300 + 20∙500 + 13∙700 + 18∙1000) = 360.

S₁΄² = 35∙(100 – 370)² + 25∙(300 – 370)² + 13∙(500 – 370)² +10∙(700 –

– 370)² + 12∙(1000 – 370)² = 8,74∙10⁶ ч²;

S₂΄² = 64∙(100 – 360)² + 35∙(300 – 360)² + 20∙(500 – 360)² +13∙(700 –

– 360)² + 18∙(1000 – 360)² = 13,72∙10⁶ ч²;

S = 301 ч; Δ = 370 – 360 =10 ч;

t = ;k = 100 + 150 – 1 = 249 (> 20);

S(t) = 0,601 < 0,975. Расхождение между выборочными средними несущественно, и обе вы­борки могут считаться принадлежащими к одной генеральной совокупности.

Фрагмент таблицы значений S(t) (критерий Стьюдента) приведен в табл.19.

Таблица 19

t	k
	10	15	20	∞
0,0	0,500	0,500	0,500	0,500000
0,1	0,539	0,539	0,539	0,53983
0,2	0,577	0,578	0,578	0,57926
0,3	0,614	0,616	0,616	0,61791
0,4	0,651	0,652	0,653	0,65542
0,5	0,686	0,688	0,689	0,69146
0,6	0,718	0,721	0,722	0,72575
0,7	0,749	0,752	0,754	0,75804

Проверка на однородность производится для всех серий ис-пытаний (выборок), после чего те серии, расхождение между выбо-рочными средними которых несущественно, могут быть объединены в одну общую серию (выборку). Дальнейшая об­работка результатов испытаний производится в зависимости от поставленной задачи.

При испытаниях радиоэлектронной аппаратуры результаты наиболее часто обрабатываются либо с целью выявления закона рапределения наработки, либо с целью определения такого диапазона изменения некоторого параметра, в котором этот па­раметр будет находиться с заданной (доверительной) вероят­ностью. Первая из поставленных задач решается в приведенной ниже последова-тельности:

1) выбирается теоретический вид плотности распределения; при этом следует исходить из общих соображений о механизме возникновения исследуемого явления (например, отказа), так: при исследовании внезапных отказов ЭС в качестве теоретического вида распределения следует выбирать экспоненциальное распределение, а при исследовании постепенных отказов – нормальное и т.д.;

2) определяются параметры теоретического вида плотности вероятности по статистическим данным с использованием формул:

; ;

3) определяется ширина интервала группирования Δx по фор­муле

;

после чего величина Δx округляется до ближайшего мень­шего удобного значения (Δx΄);

- определяется число интервалов п по формуле (в этой формуле символ [z] обозначает при дробном z – его целую часть, а при целом z – (z – 1)

, где ;

- находятся границы интервалов по формулам

- определяются теоретические частоты по формулам (если теоретическое распределение является усеченным, то пользуются только первой из формул приведенной ниже системы уравнений, полагая в ней i = 0 и i = n – 1)

- определяются эмпирические частоты по формуле

;

- определяется значение χ² по формуле

;

- определяется число степеней свободы k по формуле

k = n – r – 1,

где r – число параметров в теоретическом виде плотности вероятности;

- по известным величинам χ² и k по таблице определяется величина Р(χ²);

- по найденному значению Р(χ²) в соответствии с заранее установленными нормами (обычно полагают, что теоретиче­ское распределение согласуется со статистическими данными, если Р(χ²) ≥ 0,3) определяют степень согласования теорети­ческого и эмпирического распределений.

При оценке принадлежности двух выборок одной генераль­ной совокупности может быть использована приведенная выше мето-дика со следующими изменениями:

- операции по пп. 1 и 2 не производятся;

- величина Δx выбирается наименьшей, а величина п – наибольшей из величин, подсчитанных для обеих выборок;

- границы интервалов для обеих выборок устанавливаются одинаковыми;

- значение χ² определяется по формуле

,

где т_i1 и т_i2 – эмпирические частоты первой и второй выбо­рок в i-ом интервале;

- число степеней свободы k определяется по формуле

k = n – 1.

Пример 3. Проверить справедливость предположения о при-надлежности обеих выборок предыдущего примера к одной гене-ральной совокупности с использованием критерия χ² Пирсона [Р(χ²) ≥ 0,3].

Решение. В соответствии с приведенной методикой найдем: n=5; k = 5 – 1 = 4.

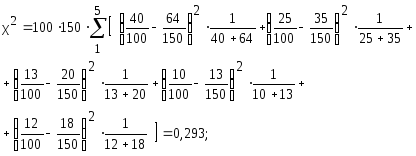
Р (χ²)  0,99 > 0,3. Предположение о принадлежности обеих выборок одной генеральной совокупности хорошо согласуется с результатами испытаний.

Вторая из поставленных задач при неизвестном виде рас­пределения исследуемого параметра решается после выбора довери-тельного интервала. Доверительный интервал обычно опре­деляется величинами вероятностей ошибок α и β. α заключается в том, что на основании результатов испытаний изделия с до­пустимыми значе-ниями параметров будут забракованы и на­зывается риском постав-щика. β заключается в том, что на основании результатов испытаний изделия с недопустимыми значениями параметров не будут забрако-ваны, и называется риском заказчика. Вместо величин α и β иногда вводят более общие величины вероят­ностей ошибок: γ₁, заклю-чающуюся в том, что значение параметра, опреде­ленное в резуль-тате испытаний, окажется меньше истинного, и γ₂, заключаю­щуюся в том, что значение параметра, определенное на основании результа­тов испытаний, окажется больше истинного. Последовательность решения следующая:

- устанавливается предположительный теоретический вид плотности распределения исследуемого параметра и опреде­ляется его согласие со статистическими данными;

- определяется среднее значение исследуемого параметра ͞x по формуле ;

- по известным величинам N, α и β (или γ₁ и γ₂ ) по таблицам для экспоненциального распределения определяются величины δ₁ и δ₂ (величины α и β или γ₁ и γ₂ выбираются в зави-симости от конкретных требований к приемке изделий; величины α, β, γ₁ и γ₂ обычно принимаются равными: 0,20; 0,10; 0,01; 0,005).

При распределении Эрланга величины δ₁ и δ₂ находятся по тем же таблицам при N₁ = kN (k – параметр распределения Эрланга); для других распределений δ₁ и δ₂ находятся по специальным таблицам или другими методами;

- определяется доверительный интервал по формуле

.

Пример 4. Определить доверительный интервал для вели-чины наработки до отказа T₀ ЭС (вторая серия испытаний при­мера 2) при α = β = 0,10. Предполагается, что наработка до отказа распре-де­лена по экспоненциальному закону.

Решение. Имеем: N = 150; x = 360 ч; δ₁=0,897; δ₂=1,11.

Получаем доверительный интервал для T₀ 324 ч ≤ T₀ ≤ 401 ч.

Фрагменты таблиц для δ₁ и δ₂ приведены в табл.20.

Таблица 20

N	δ1				δ2
	α = 0,05	α = 0,10	α = 0,20	α = 0,05		α = 0,10	α = 0,20
10	0,543	0,622	0,729	1,57		1,42	1,25
100	0,841	0,874	0,915	1,17		1,13	1,08
150	0,870	0,897	0,931	1,14		1,11	1,07
200	0,887	0,911	0,940	1,12		1,09	1,06

В тех случаях, когда целью испытаний является определение величины коэффициента корреляции, достоверность полученных результатов определяется с помощью критерия Z Фишера в по­следовательности, указанной ниже (N – объем выборки):

- по известной величине r по таблицам (например, [2]) определяется величина ;

- определяется величина σ_r по формуле ;

- определяется величина t по формуле t = z / σ_r;

- по известной величине t по таблицам функции

определяется величина 0,5 Ф(t);

- оценивается случайность отклонения величины r от 0:

если 0,5∙Ф(t) < (1 – β) / 2, то отклонение величины r от 0 несущественно,

если 0,5∙Ф(t) ≥ (1 – β) / 2, то отклонение величины r от 0 существенно.

Определение доверительного интервала для величины r про­изводится аналогично процедуре, описанной выше, с той разницей, что доверительный интервал определяется для величины Z, а затем, с помощью таблиц по найденным значениям Z – для величины r.

Пример 5. В результате обработки результатов 1000 наблю-дений найдена величина коэффициента корреляции r = 0,16.

Определить доверительный интервал для r при доверитель-ной вероятности (1 – β), равной 0,95.

Решение. Имеем: Z = 0,5∙ln((1+0,16) / (1 – 0,16) = 0,1614; σ_r = 1 / (1000 – 31)^0,5 = 0,0321; t = 0,1614 / 0,0321 = 5,028; 0,5∙Ф(t) = = 0,4999998 > 0,475.

Отклонение коэффициента корреляции от 0 существенно. Доверительный интервал

Z – 1,96∙σ_r ≤ Z₀ ≤ Z + 1,96 σ_r; 0,0985 ≤ Z₀ ≤ 0,2243;

0,098 ≤ r₀ ≤ 0,220.

В табл.21 приведен фрагмент таблицы значений Z.

Таблица 21

r	0	1	2	3	4	5	6	7	8	9
0,0	0,0000	0,0100	0,0200	0,0300	0,0400	0,0501	0,0601	0,0701	0,0802	0,0902
0,1	0,1003	0,1104	0,1206	0,1308	0,1409	0,1511	0,1614	0,1717	0,1820	0,1923
0,2	0,2027	0,2132	0,2237	0,2342	0,2448	0,2554	0,2661	0,2769	0,2877	0,2986