3.5.3. Задачник 2. Расчеты и преобразования схем надежности

Все задания сведены в таблицу 22 в соответствии со студенческим шифром (последние две цифры). Требуется рассчитать показатель безотказности, указанный в таблице в столбце «Требуется рассчитать». Для этого следует руководствоваться материалом, представленным в учебном пособии [1].

Среднее значение наработки на отказ рассчитывается по формуле , где – математическое ожидание числа отказов восстанавливаемого изделия в единицу времени для установившегося процесса эксплуатации.

Значения вероятности безотказной работы вычисляются по

формуле , гдеt – время, за которое требуется рассчитать вероятность безотказной работы. Работа выполняется в тетради или на листах формата А4.

Содержание отчета

1. Исходные данные, вариант. Цель расчета.

2. Пояснения и сам расчет с приведением формул и схем в

виде рисунков.

3. Анализ полученных результатов (вывод).

Таблица 22

Исходные данные
По последней цифре студенческого шифра		По предпоследней цифре студенческого шифра
№ п/п	Схема надежности изделия	Значения вероятностей безотказной работы элементов схем	Требуется рассчитать
1		P1 = P2 = P5 = P7 = 0,9 P3 = P4 = P6 = 0,8	T
2		P1 = P2 = P5 = P7 = 0,9 P3 = P4 = P6 = PР = 0,8	P(t) t = 24 ч
3		P1 = P2 = P5 = P6 = 0,8 P3 = P4 = P7 = PР = 0,9	T
4		P1 = P2 = P5 = P7 = 0,9 P3 = P4 = P6 = PР = 0,7	P(t) t = 16 ч
5		P1 = P2 = P5 = P7 = 0,7 P3 = P4 = P6 = PР = 0,7	T
6		P1 = P2 = P5 = P7 = 0,8 P3 = P4 = P6 = 0,7	P(t) t = 8 ч
7		P1 = P2 = P5 = P7 = 0,7 P3 = P4 = P6 = PР = 0,8	T
8		P1 = P2 = P5 = P7 = 0,9 P3 = P4 = P6 = PР = 0,8	P(t) t = 12 ч
9		P1 = P2 = P5 = P7 = 0,8 P3 = P4 = P6 = PР = 0,6	T
0		P1 = P2 = P5 = P7 = 0,9 P3 = P4 = P6 = PР = 0,8	P(t) t = 10 ч

Примечание. В таблице обозначены: цифрами от 1 до 7 – элементы, буквой «Р» – разъем, а P_i – вероятности безотказной работы элементов схем изделия;T – наработка на отказ; P(t) – вероятность безотказной работы за время t

Порядок представления расчетов – см. с. 101 – 102.

Методические указания к выполнению практических занятий по расчетам и преобразованиям схем надежности

1. Цель работы – приобретение практических навыков расчета сложных схем надежности.

2. Основные теоретические положения. Структурное резервирование использует структурные модели надежности, которые представляют собой графические изображения структур ЭС, в которых выделены элементы и связи, выполняющие основные функции данного устройства. В структурной схеме модели элементы и связи выделяются не по конструктивному, а по функциональному признаку, исходя из условия, чтобы каждому функциональному элементу обеспечивалась независимость, т.е. чтобы отказы любого функционального элемента не зависели и не предопределяли отказы всех остальных. При составлении моделей конструктивные элементы, от-казы которых взаимосвязаны, объединяют. Простейшими, наиболее универсальными и представительными моделями надежности являются последовательные и параллельные системы, состоящие из независимых элементов.

Последовательная модель надежности. Последовательным, в смысле надежности, называют такое соединение элементов в системе, при котором отказ хотя бы одного элемента приводит к отказу всей системы. Причем это не обязательно означает, что реальное соединение элементов будет последовательным. Например, если элементы электрической схемы соединены параллельно, но отказ их имеет характер короткого замыкания, то в смысле надежности эти элементы соединены последовательно. Рассматривается расчетный случай, когда отказы элементов считаются независимыми. Модель представлена на рис.5. Обозначим соответственно вероятности безотказной работы подсистем P₁(t); P₂(t); …; P_n(t), тогда вероятность безотказной работы всей системы P_с(t) найдем как

а вероятность появления в ней отказа

Если вероятности всех подсистем одинаковы и равны, то выражение дляP_с примет вид P_c(t) = Pⁿ(t).

p₁(t)

p₂(t)

p_n(t)

- -

Рис.5. Последовательная модель надежности

Экспоненциальное распределение. В этом случае

,

где λ_i и Λ – интенсивность отказов соответственно элементов и системы. Таким образом, можно написать: , т.е. вероятность безотказной работы последовательного соединения элементов не может быть больше вероятности безотказной работы наименее надежного элемента.

Параллельная модель надежности. Она отображает систему, состоя­щую из двух и более подсистем, соединенных параллельно. От­личительным признаком этой модели является условие работоспо­собности, состоящее в том, что реальная система остается работо­способной, если хотя бы одна из подсистем исправна. Такая мо­дель может быть проиллюстрирована структурной схемой, представ­ленной на рис.6; здесь обозначения p₁(t), ..., p_n(t) имеют тот же физический смысл, что и в последовательной модели.

Основная система

p₁(t)

p₂(t)

p_n(t)

Резервные подсистемы

Рис.6. Параллельная модель надежности

Вероят­ность безотказной работы всей системы P_c(t) и веро-

ятность возникновения в ней отказа Q_с(t) этом случае равны:

При одинаковых вероятностях безотказной работы всех элементов параллельной системы [p_i(t) = p(t)] выражения для P_c(t) и Q_c(t) приобретут соответственно вид

P_c(t) = 1 – [1– p(t)]ⁿ; Q_c(t) = [1– p(t)]ⁿ.

В этом случае можно записать:, т.е. вероятность безотказной работы параллельного соединения элементов не может быть меньше вероятности безотказной работы наиболее надежного элемента.

Сложность и трудность расчетов надежности ЭС вызываются тем, что структура исследуемых объектов сложная. Поэтому всегда, как правило, прежде чем начинать расчет надеж­ности, необходимо посмотреть, нельзя ли преобразовать сложную структуру, сделать ее более простой и удобной для расчетов. Наи­более удобной структурой является структура, состоящая из по­следовательно соединенных или параллельно соединенных эле­ментов.

В математической логике доказывается, что любые логические операции могут быть заменены тремя простейшими: дизъюнкцией, конъюнкцией и отрицанием. Дизъюнкции соответствует параллель­ное соединение элементов, конъюнкции – последовательное. От­сюда следует, что любую структуру можно представить в виде на-бора последовательно-парал­лельных структур. Но практически на пути таких структурных пре­образований возникают серьезные трудности. Структурный анализ систем составил самостоятельное научное направление. В нем ис­пользуются математическая логика, теория графов, теория матриц и др. Укажем некоторые важные положения и рекомендации теории структурного анализа, входящие в теоретическую основу расчетов надежности ЭС [1, 12].

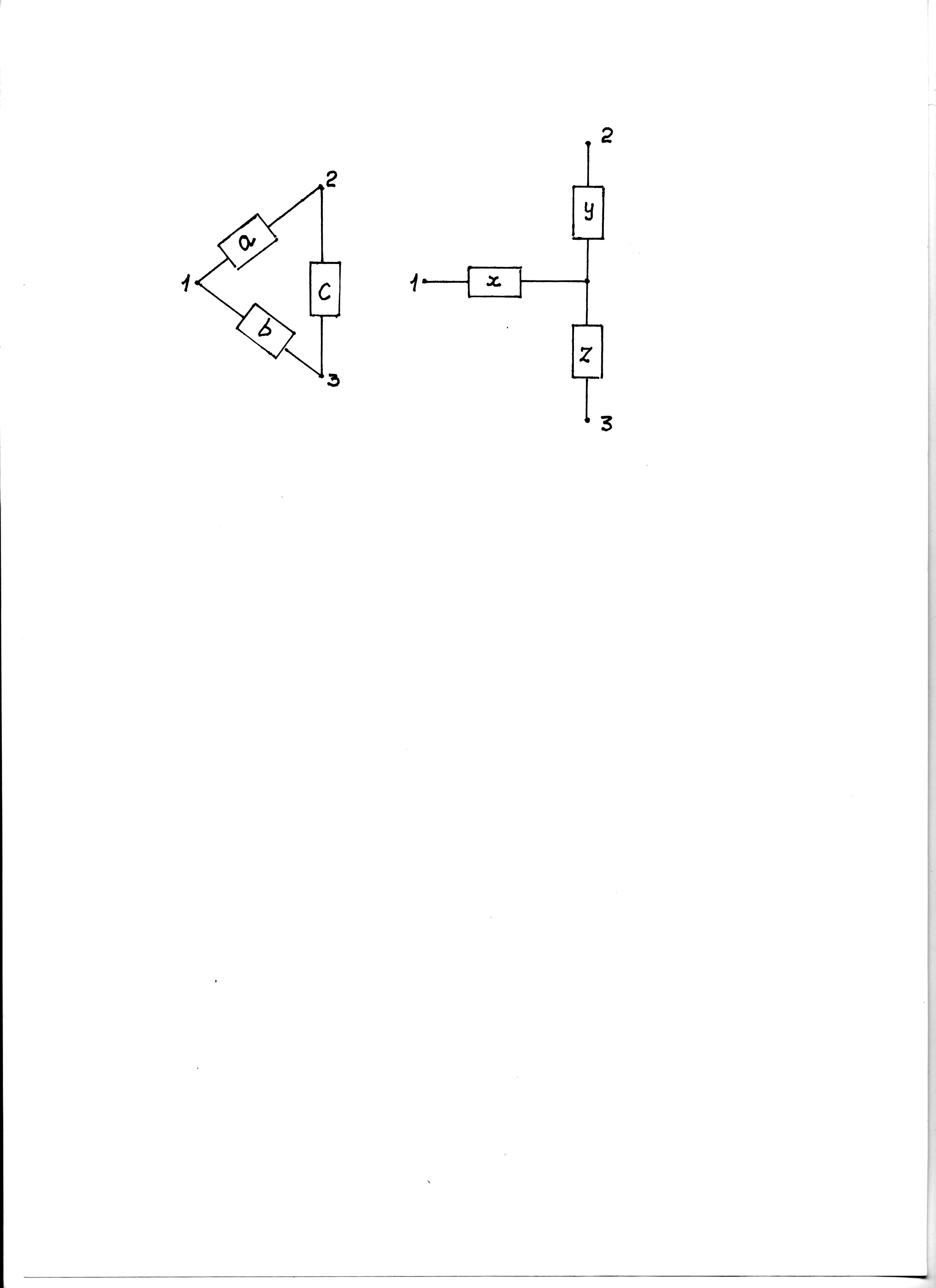
Преобразование структуры типа «треуголь­ник» в структуру типа «звезда». Исходную структуру типа «треугольник» (рис.

7, а) необходимо преобразовать в «звезду» (рис.7, б). Чтобы «звезда» была эквивалентной «треугольнику», необходи­мо обеспечить эквивалентность уравнений работоспособности «треугольника» и «звезды», т.е. следующие равенства:

(36)

где а, b, с, х, у – события, состоящие в том, что элементы находят­ся в работоспособном состоянии, а знак логического сложения определяется, например, для a˅b∙c, как a + bc – abc.

а б

Рис.7. Преобразование струк­туры типа «треугольник» (а) в

структуру типа «звезда» (б)

Из (36) следует, что вероятности работоспособного состояния цепей 1-2, 1-3 и 2-3 должны быть равны как для «треуголь­ника», так и для «звезды». Поэтому

. (37)

Рассмотрим случай, когда . Тогда система уравнений (37) упрощается:P_т + P_т² – P_т³ = P_з².

Пример 1. Определить вероятность работоспособного состояния элемен­та «звезды», полученной при преоб­разовании «треугольника», если веро­ятность работоспособного состояния каждого

элемента «треугольника» равна 0,9.

Вероятность работоспособного со­стояния элемента «звезды»

Пример 2. Определить вероятность безотказного состояния мостиковой схе­мы (рис.8, а), если вероятность безотказного состояния каждого из ее эле­ментов равна Р = 0,8.

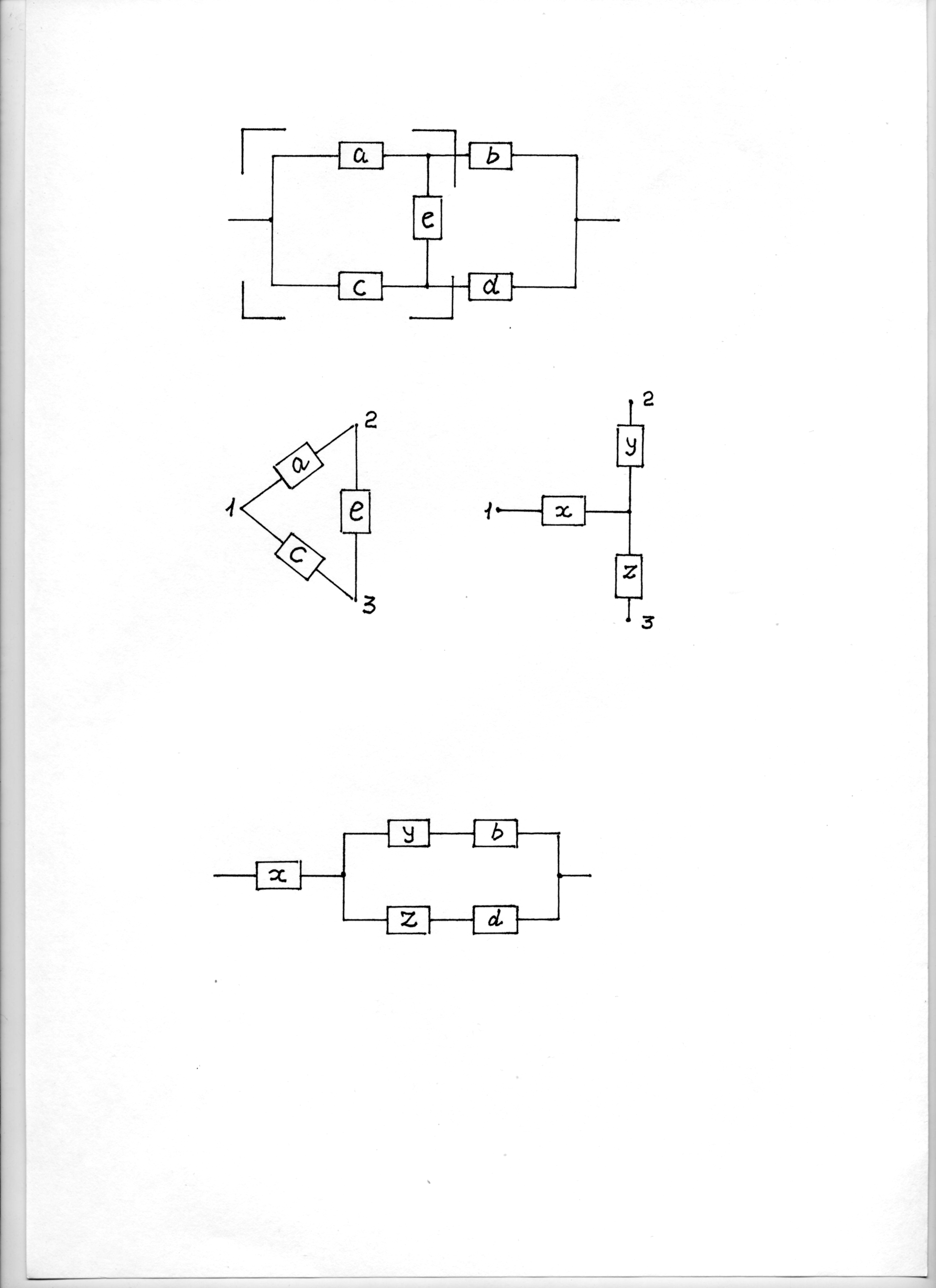
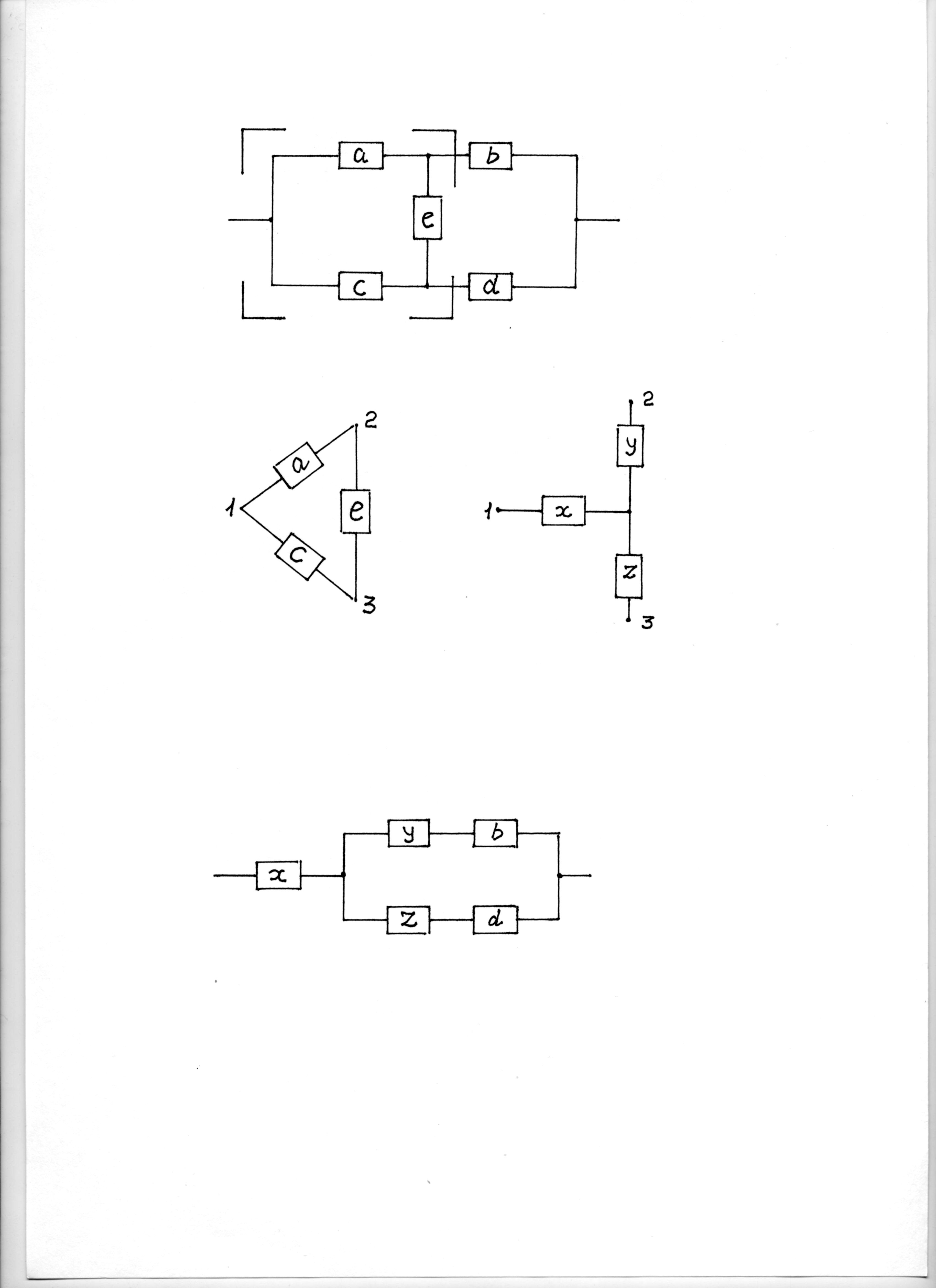
а б

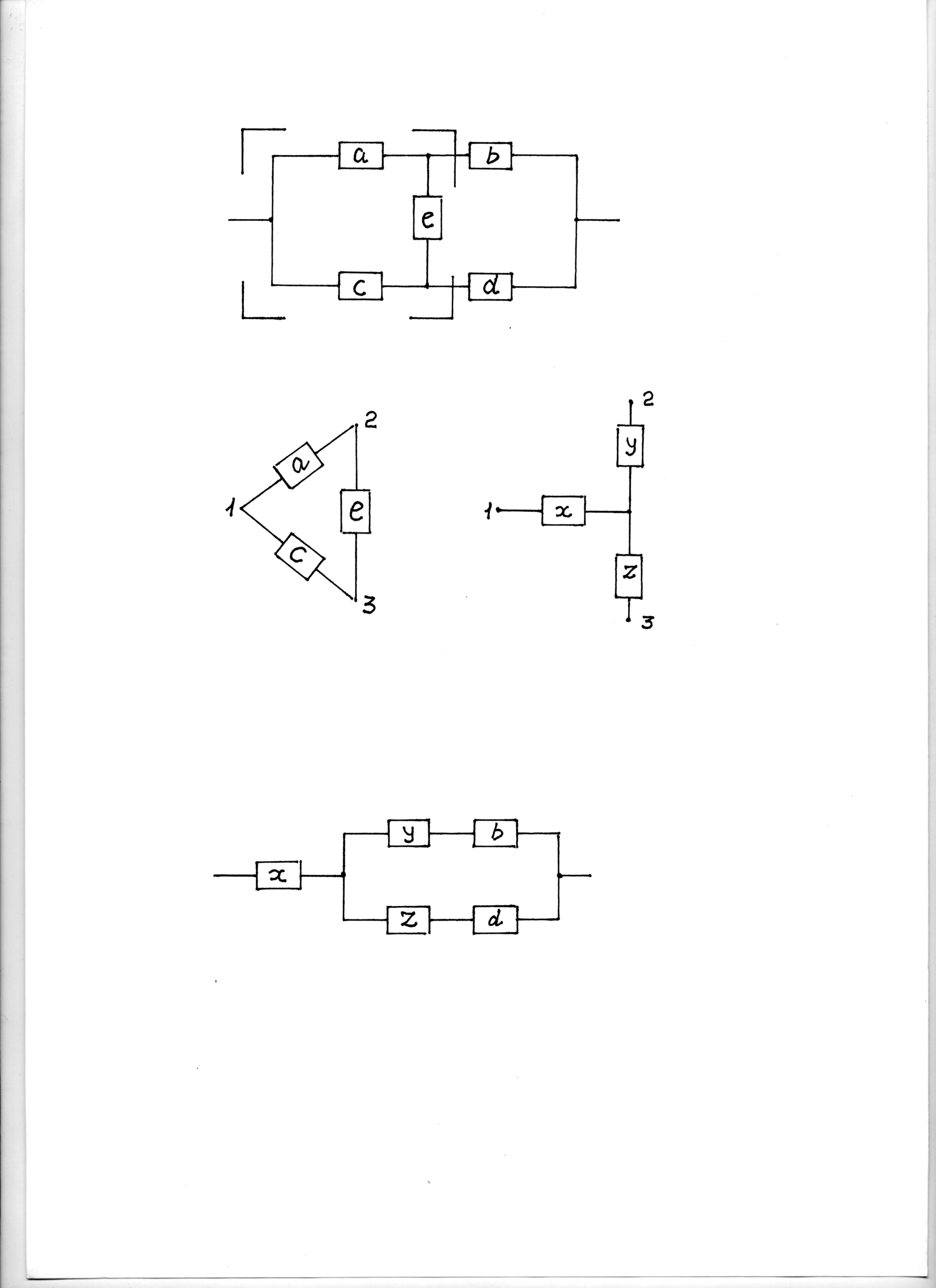
в

Рис.8. Преобразование схемы мостиковой в схему

последова­тельно-параллельную

Преобразуем группу элементов а, е, с, соединенных по схеме «треугольника», в «звезду» (рис.8, б). Тогда вероятность безотказного состояния элемента «звезды» P_з == 0,96 =P_x = P_y = = P_z. В результате преобразования группы элементов а, е, с в «звезду» мостиковая схема преобразуется в схему последовательно-параллельную (рис.8, в). Вероятность безотказного состояния мостиковой схемы равна вероятности безотказного состояния схемы, показанной на рис.8, в: P = P_x[P_yP_b + P_zP_d – P_yP_b P_zP_d ] = 0,91.

Метод разложения сложной структуры по «ключевым элементам». По этому методу сложная структура заменяется двумя более простыми структурами, такими, что сумма вероятностей работоспособных состояний этих структур равна вероятности работоспособного состояния исходной структуры. В основу метода положена или формула разложения логического уравнения работоспособности, или вытекающая из нее формула вероятности полного события.

Пусть, например, требуется разло­жить мостиковую схему (рис.9, а) на две составляющие схемы. Примем в качестве «элемента разложения» элемент е. Предположим, что элемент е находится в ра-ботоспособном состоянии. В этом случае вместо элемента е можно поставить жесткую связь и мостик преобразуется в схему, изображенную на рис.9, б, но к этой схеме необходимо последовательно присоединить элемент е с тем, чтобы учесть, что вероятность рабо­тоспособного состояния элемента е P_е не равна 1. В результате окон-чательно по­лучим схему, показанную на рис.9, б. Но элемент е может на­ходиться в состоянии отказа. Тогда на мостиковой схеме его поло­жение следует обозначить обрывом цепи. В результате с учетом вероятности отказа элемента е получим схему, изображенную на рис.9, в. Схемы, показанные на рис.9, б, в, являются схе­мами, заменяющими мостиковую схему. Они значительно проще ее по своей конструкции.

a

b

e

c

d

а

a

bb

a

bb

ee

͞е

е

cc

dd

cc

dd

б в

Рис.9. Разложение мости­ковой схемы на две составля­ющие схемы

Примечание. В случае необходимости разложение структуры произво­дится многократно. Например, если полученная на этапе 2 первая структура, в свою очередь, окажется чрезмерно сложной, ее можно разложить на структуры третью и четвертую.

Пример 3. Определить вероятность безотказного состояния мостиковой схе­мы (рис.9, а), используя метод разложения схемы по ключевому элементу. Вероятность безотказного состояния каждого из элементов схемы равна 0,8.

Решение. Элемент разложения – е. Первая структура, полученная в результате разложения, изображена на рис.9, б, а вторая структура – на рис.9, в. Вероятность безотказного состояния первой структуры P₁ = 0,734. Вероятность безотказного состояния второй структуры Р₂ = 0,176. Вероятность безотказного состояния мостиковой схемы P₃ = 0,91.