statistika_проц_22

Пример 5.8. В результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было 3942 кг, что составляет 70,4 % общего веса муки этой партии. Во второй партии муки высшего сорта было 6520 кг, что составляет 78,6 % общего веса муки этой партии. Определите процент муки высшего сорта в среднем по первой и второй партиям вместе.

Решение

Исходное соотношение средней представляет собой в данном слу- чае отношение веса муки высшего сорта в двух партиях к общему весу муки.

Средний процент муки высшего сорта по двум партиям определяем по формуле средней гармонической взвешенной:

			=	3942 +		6520		=		10462	= 0,753, èëè 75,3 %.
		x
				3942	+		6520		13894,6
				0,704		0,786

5.5. Средняя геометрическая

ный депозит, процент по которому ежегодно изменяется. После каждого года сумма, равная процентному приросту, добавляется к сумме счета. Например, первоначальная сумма вклада составила 100 денежных единиц. За первый год вы получили 5 % дохода по вкладу, за второй 7 %, за третий

9 % и за 4-й — 10 %. Каков средний уровень дохода по вкладу за 4 года?Пример 5.9. Предположим, вы внесли деньги в банк на сроч-

Можно сложить и вычислить среднюю арифметическую величи-

	ну дохода:		=	0,05 + 0,07 +	0,09 + 0,10	= 0,0775, èëèë7,75.	%.
		x
				4

Верно ли это?

Введем следующие условные обозначения: P — первоначальная сумма вклада, i1,i2 ,i3 ,i4 — доход по вкладу в первый, второй, третий и четвертый годы соответственно (в долях единиц), F — сумма вклада по истечении четырех лет.

151

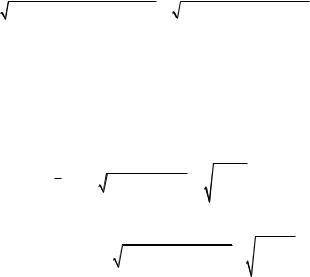
Если первоначальная сумма вклада — Р, то после первого года она возрастает и становится

P×(i1 +1) =100×(0,05 +1) =105. В конце второго года эта сумма составит

P×(i1 +1)×(i2 +1) =100×(0,05 +1)×(0,07+1) =112,35. В конце третьего года:

P×(i1 +1)×(i2 +1)×(i3 +1) =100×(0,05 +1)×(0,07 +1)×(0,09 +1) =122,4615. По истечении четырех лет сумма составит

F= P×(i1 +1) ×(i2 +1) ×(i3 +1)×(i4 +1) =

=100×(0,05 +1) ×(0,07+1)×(0,09 +1)×(0,10 +1) = 134,70765.

Если необходимо определить средний процент дохода i, который даст сумму дохода F по истечении четырех лет, при прибавлении ежегодного накопленного прироста к сумме вклада, то это будет величина, которая определится из следующего уравнения:

(i + 1)4 = (1 + i1)(1 + i2)(1 + i3)(1 + i4)(1 + i5). Решение этого уравнения находится по формуле:

(i +1) = 4 (1+ i1)(1+ i2)(1+ i3)(1+ i4) = 4 1,05×1,07×1,09×1,10 = 1,0773282,

ãäå (i +1) — геометрическая средняя из (1+ i1)(1+ i2)(1+ i3)(1+ i4) . Средний процент дохода по вкладу равен

(1−1,0773282) ×100 ≈ 7,733 % ,

что отличается от результата, полученного по средней арифмети- ческой.

Общий вид формулы средней геометрической невзвешенной:

n

xãåîì = n x1 x2 ... xn = n ∏xi . i=1

Средней геометрической взвешенной:

			∑fj				=∑		m
				f1	f2	fm		fj	fj
	xãåîì =									.
				x1	x2	... xm			∏ xj
									j=1

(5.11)

(5.12)

Согласно правилу мажорантности средней, расчет по средней арифметической завышает результат; чем длиннее период расче- та, тем больше будет ошибка.

152

Пример 5.10. В результате инфляции за первый год цена товара возросла в два раза к предыдущему году, а за второй год еще в три раза к уровню предыдущего года. Ясно, что за два года цена возросла в 6 раз. Каков средний темп роста цены за год?

Решение

Арифметическая средняя здесь непригодна, поскольку, если за год цена выросла бы в (2 + 3)/2 = 2,5 раза, то за два года цена выросла бы в 2,5 ½ 2,5 = 6,25, а не в 6 раз. Геометрическая средняя даст правильный ответ: 6 = 2, 45 ðàçà.

Геометрическая средняя дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака.

Пример 5.11. Максимальный выигрыш в лотерее составляет миллион рублей, а минимальный — сто рублей. Какую вели- чину можно считать средней между миллионом и сотней?

Решение

Арифметическая средняя явно непригодна, так как составляет 500050 рублей, а это, как и миллион, крупный, а никак не средний выигрыш. Геометрическая средняя в этом случае дает наиболее правильный с точки зрения экономики и логики ответ:

100 100000 = 10000 ðóá.

Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе.

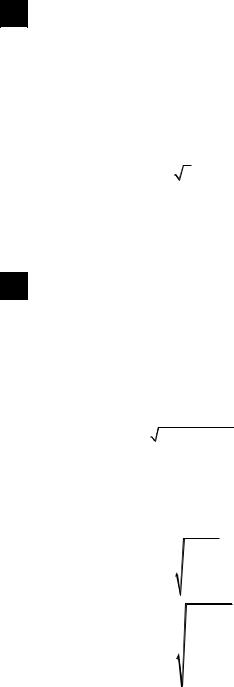
Средняя квадратическая. В основе вычислений ряда сводных рас- четных показателей лежит средняя квадратическая:

				n
xквадр =			∑xi2			— невзвешенная		(5.13)
				i=1
				n
				m
				∑x2j fj
				j=1
xквадр =							— взвешенная	(5.14)
				m
				∑ fj

j=1

153

Наиболее широко этот вид средней используется при расчете показателей вариации.

В статистическом анализе также применяются степенные средние 3-го порядка и более высоких порядков.

5.6. Показатели структуры вариационного ряда. Меры центральной тенденции

При изучении статистической совокупности применяются такие ее характеристики, которые описывают количественно ее структуру, строение.

Квантили — это варианты, занимающие определенное место в ранжированной совокупности. К числу квантилей, наиболее часто используемых в статистическом анализе, относят перцентили, квартили, децили и медиану, которые характеризуют структуру совокупности.

Перцентиль — это значение признака в определенной позиции ранжированного ряда, мера относительной позиции варианта в ряду. Р-тый перцентиль — это значение признака, слева от которого лежит Р % вариантов ряда. Позиция Р-го перцентиля задается как (n + 1)Р/100, где n —число вариантов ряда.

В статистике наиболее часто применяются квантили, которые делят ряд на четыре равные части — квартили (от латинского слова quarta — четверть).

Первый квартиль (25-й перцентиль) — это значение признака, слева от которого лежит 1/4 (или 25 %) всех вариантов.

Второй квартиль — это 50 перцентиль или медиана.

Медиана — значение признака, относительно которого совокупность делится на две равные по числу вариантов части.1

Третий квартиль — это точка, слева от которой находится 3/4 или 75% вариантов ряда.

25-й перцентиль называют — нижним квартилем (Q1), 50-й перцентиль (медиану) — средним квартилем (Q2), 75-й перцентиль —

верхним квартилем (Q3).

В статистическом анализе также часто применяют квантили, которые делят совокупность на десять равных частей — децили. Их зна- чения определяются соответственно как 10, 20, ..., 90-е перцентили.

1Медиана обладает свойством: сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины, т.е. ∑õi — Ìå = min.

154

В общем случае квантили интервального вариационного ряда определяются по формуле:

Q	= x		+ k	P∑ fi	− VQp−1	,	(5.15)
		Qp(min)
p				fQp

ãäå xQp(min) — нижняя граница интервала, в котором находится кван-

òèëü;

k — величина квантильного интервала (интервальная разность);

VQp−1 — накопленная частота или частость интервала, предше-

ствующего квантильному; Р — доля признаков, находящихся левее квантиля (например,

для верхнего квартиля — 0,25, для медианы — 0,5, для седьмого дециля — 0,7);

∑ fi — сумма всех частот;

fQp — частота квантильного интервала.

Для расчета значения медианы в интервальном вариационном ряду вначале находят интервал, содержащий медиану. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. Внутри медианного интервала расчет значения медианы производится по

	формуле:		0,5∑ fi	− vMe−1
	Ìå = xMe min	+ k			,	(5.16)
			fMe

ãäå xMe min — нижняя граница медианного интервала; k — величина медианного интервала;

0,5∑ fi — половина суммы всех частот (или частостей);

vMe−1 — накопленная частота или частость интервала, предшествующего медианному;

fMe — частота медианного интервала.

Мода — это значение признака, наиболее часто встречающееся в совокупности. В интервальном вариационном ряду мода рассчитывается по следующей формуле:

155

	Ìî = xMî min + k		fMo	− fMo−1	,	(5.17)
		(fMo	− fMo−1) + (fMo − fMo+1)

ãäå xMî min — нижняя граница модального интервала;

k — величина модального интервала; fMo — частота модального интервала;

fMo−1 — частота интервала предшествующего модальному; fMo+1 — частота интервала, следующего за модальным.

Пример 5.12. Правительство развивающейся страны объявило конкурс для зарубежных инвесторов на заключение контракта по строительству нового морского порта. В ответ были получены следующие предложения цены (млрд долл.): 2, 3, 2, 4, 3, 5, 1, 1, 6, 4, 9, 2, 5, 1, 6. Построить вариационный ряд, найти среднюю арифметическую, квартили и 65-ый перцентиль.

Решение

Строим вариационный ряд

	xi				1		2	3		4			5			6	7
	fi
	Рассчитаем среднюю арифметическую взвешенную:
			=	1 3 + 2 3 + 3 2 + 4 2 + 5 2 + 6 2 + 7 1								=	52		= 3,47 ìëðä äîëë.
		x
						3 + 3 + 2 + 2 + 2 + 2 +1							15

Определим первый квартиль или 25-й перцентиль. Позиция этого перцентиля: (15 + 1) ½ 0,25 = 4. Четвертое по порядку значение равно 2, т. е. Q1 = 2.

Определим второй квартиль или 50-й перцентиль, т.е. медиану. Позиция этого перцентиля: (15 + 1) ½ 0,5 = 8. Восьмое по порядку значение равно 3, т. е. Q2 = Ìå = 3.

Определим третий квартиль или 75-й перцентиль. Позиция этого перцентиля: (15 + 1) ½ 0,75 = 12. Двенадцатое значение признака равно 5, т. е. Q3 = 5.

Позиция 65-го перцентиля: (15 + 1) ½ 0,65 = 10,4. Десятый по порядку вариант равен 4, а одиннадцатый равен 5. Значение 65-го перцентиля находится в точке, которая делит расстояние десятым

156

и одиннадцатым признаком в отношении 0,4 к 1. Следовательно Р65 = 4 + 0,4(5 – 4) = 4,4.1

Пример 5.13. Имеются данные о числе цветных телевизоров, проданных в течение 26 дней:

16; 12; 15; 15; 23; 9; 15; 13; 14; 14; 21; 15; 14; 17; 27; 15; 16; 12; 16; 19; 14; 16; 17; 13; 14; 14.

1)Расположите данные в возрастающем порядке

2)Определите 25-й; 50-й и 90-й перцентили, нижний, средний и верхний квартили.

3)По ранжированным данным составьте дискретный вариационный ряд распределения частот.

4)Составьте дискретный вариационный ряд частостей.

5)Составьте интервальный вариационный ряд частот.

6)Постройте полигон дискретного вариационного ряда частот.

7)Постройте гистограмму интервального вариационного ряда частот.

8)Вычислите моду для дискретного вариационного ряда частот.

9)Найдите медиану и моду для интервального вариационного ряда частот.

10)Рассчитайте среднее число проданных цветных телевизоров по формуле для дискретного и интервального рядов.

Решение

1) Ранжируем данные:

9; 12; 12; 13; 13; 13; 14; 14; 14; 14; 14; 14; 15; 15; 15; 15; 15; 16; 16; 16; 17; 17; 19; 21; 23; 27.

x1 = 9; xn = x26 = 27.

2) Определим 25-й, 50-й и 90-й перцентили для этого вариационного ряда.

Для определения 25-го перцентиля необходимо сначала найти его позицию в вариационном ряду:

n = 26.

По определению Ð -перцентия имеем:

(n + 1)100P = (26 + 1)10025 = 27 0,25 = 6,75.

1Квантили не всегда совпадают с определенными вариантами. Квантиль — это либо вариант ряда, либо промежуточное значение между двумя соседними вариантами.

157

Эта позиция находится между шестым и седьмым вариантами. Шестой по порядку вариант в ранжированном ряду равен 13, седьмой — 14. Значение перцентиля находится в точке, которая делит расстояние между 13 и 14 в отношении 0,75 к 1, т. е. расстояние от 13 до 25-го перцентиля составляет 0,75 от длины отрезка между 13 и 14. Итак, 25-й перцентиль равен 13,75.

Для того, чтобы найти 50-й перцентиль, мы должны определить значение варианта, соответствующего позиции:

(n + 1)100P = (26 + 1)10050 = 27 0,5 = 13,5.

Среди ранжированных вариантов значение 13-го по порядку варианта равно 15, а значение 14-го варианта так же равно 15, отсюда, 50-й перцентиль равен 15.

Имеем:

Q25 = 13,75 ; Q50 = 15 .

Аналогично определим 90-й перцентиль (Q90) как значение варианта, соответствующего позиции

(n + 1)100P = (26 + 1)10090 = 27 0,5 = 24,3.

Значение 24-го варианта равно 19, а 25-го — 21, Следовательно, расстояние от 19 до 90-го перцентиля составляет 0,3 от длины отрезка между 19 и 21 (длина отрезка равна двум). Итак Q90 = 19,6 .

Первый (нижний) квартиль — это 25-й перцентиль, т.е. значе- ние признака в вариационном ряду, слева от которого лежит 1/4 (или 25%) всех вариантов.

Второй (средний) — это 50-й перцентиль, он же медиана (Ìå)

Q50 = 15.

Третий (верхний) квартиль — это точка, слева от которой находится 3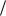4 (или 75 %) вариантов ряда. Сначала определим позицию, которой соответствует эта точка:

27 10075 = 20,65.

Таким образом, значение верхнего квартиля равно 16,65.

3) В исходных данных: 12; 13; 14; 15; 16 и 17 повторяются. Тогда вариационный ряд можно представить в виде следующей таблицы:

158

Таблица 5.6

Значения
признака (xi )	9	12	13	14	15	16	17	19	21	23	27
Число дней
(mi )	1	2	3	6	5	3	2	1	1	1	1

Âполученном ряду k = 11 , à n = ∑mi = 26.

i=111

4) Запишем дискретный вариационный ряд частостей числа цветных телевизоров, проданных в течение 26 дней:

Таблица 5.7

Значения
признака	9	12	13	14	15	16	17	19	21	23	27
(xi )
Число
äíåé (wi )	0,04	0,08	0,11	0,23	0,19	0,11	0,08	0,04	0,04	0,04	0,04

k=11

∑wi = 1.

i=1

5)Для данных примера 1.1 xmin = 9, à xmax = 27 и число интервалов L = 1 + 3,322lg n = 1 + 3,322 1,41497 = 5,7005 ≈ 6.

Находим ширину интервалов разбиения (ki) ki = 276−9 = 3.

Если бы оказалось, что ki — дробное число (например, 3,9576), то за ширину интервала надо брать либо ближайшее целое число 4, либо ближайшую простую дробь ≈ 3,96, ограничиваясь двумя знаками после запятой.

Теперь построим вариационный ряд границ интервалов группирования без корректировки границ первого и последнего интервалов, т.е. к xmin прибавляем 3 и получаем первый интервал от 9 до 12. И последующие интервалы получаются прибавлением к концу предыдущего интервала ширины интервала ki. Затем подсчитываем количество вариантов mi, попавших в каждый интервал.

159

При построении интервальных рядов в каждый промежуточный интервал можно включать варианты, числовые значения которых больше нижней границы интервала и меньше или равны верхней границы (или наоборот).

Таблица 5.8

Интервалы	[9; 12]	(12; 15]	(15; 18]	(18; 21]	(21; 24]	(24; 27]
mi	3	14	5	2	1	1

6

∑mi = 26 ; L = 6 .

i=1

Например, из табл. 5.8 видно, что в третий интервал (15; 18] попало 5 вариантов.

Если же в промежуточный интервал включаются варианты, числовые значения которых больше или равны нижней границы и меньше верхней границы, то частоты интервалов будут другими:

Таблица 5.9

Интервалы	[9; 12)	[12; 15)	[15; 18)	[18; 21)	[21; 24)	[24; 27]
mi	1	11	10	1	2	1

6

∑mi = 26 ; L = 6 .

i=1

Âтретий интервал [15; 18) попало 10 вариантов.

Для того, чтобы x1 è xn попали внутрь первого и последнего интервалов группирования, начало (нижнюю границу) первого ин-

тервала рекомендуется брать как x1′ = xmin − k2i = 9 − 32 = 7,5 , à íà-

чало последнего интервала как x′n = xmax + k2i = 27 +1,5 = 28,5.

Промежуточные интервалы получаются прибавлением к концу предыдущего интервала величины интервала ki.

Сгруппированный вариационный ряд с корректировкой границ первого и последнего интервалов представим в виде следующей таблицы:

160