statistika_проц_22

Никто не обнимет необъятного.

Козьма Прутков, Плоды раздумий

Глава 7

ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ

Изучив тему, студент должен знать

■понятия выборочного метода, генеральной и выборочной совокупностей, способы отбора единиц генеральной совокупности в выборку: соб- ственно-случайный (повторный и бесповторный), механический, типи- ческий, серийный; виды ошибок статистического наблюдения; сущность теории оценивания;

■точечные оценки параметров генеральной совокупности по выбороч- ным данным;

■требования, предъявляемые к статистическим оценкам; механизм интервального оценивания параметров генеральной совокупности по выборочным данным;

■параметры интервального оценивания, вероятностный смысл статисти- ческих оценок;

■формулы расчета предельной и средней ошибок выборки при оценке генеральных средней и доли для различных способов отбора;

■формулы расчета необходимой численности выборки, понятия о малой выборке и распределении Стьюдента;

уметь

■провести точечное и интервальное оценивание неизвестных параметров генеральной совокупности по выборочным данным;

■рассчитать среднюю и предельную ошибки выборки при оценке генеральных средней и доли для различных способов отбора;

■рассчитать необходимую численность большой и малой выборок;

■пользоваться таблицами функций нормированного нормального распределения и распределения Стьюдента.

221

7.1. Основные понятия и определения выборочного наблюдения

Ряд распределения, полученный в результате сводки и группировки первичного статистического материала, может рассматриваться как эмпирическое распределение (выборка), извлеченное из генеральной совокупности с тем, чтобы судить по нему обо всей генеральной совокупности. С этой точки зрения числовые характеристики, рассчитанные по данным эмпирических распределений: средние, показатели вариации и др., представляют собой оценки показателей генеральной совокупности. Эта глава посвящена теории статистического оценивания и ее практическому приложению — выборочному методу наблюдения.

Выборочное наблюдение представляет собой один из наиболее широко применяемых видов несплошного наблюдения. При проведении выборочного наблюдения обследуются не все единицы изу- чаемого объекта (генеральной совокупности), а лишь некоторая, тем или другим случайным образом отобранная часть этих единиц (выборочная совокупность).

Таким образом, вся совокупность единиц, из которой осуществляется отбор, составляет генеральную совокупность.

Часть совокупности, случайным образом отобранная из генеральной совокупности, представляет собой выборочную совокупность — выборку.

Выборочное обследование осуществляется с меньшими затратами труда и средств и в более короткие сроки, чем сплошное наблюдение, что повышает оперативность статистической информации, уменьшает ошибки регистрации. В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции, сопровождающимся разрушением проверяемого изделия.

Хорошо организованное выборочное обследование дает достаточно точные результаты, поэтому выборка может применяться для проверки данных сплошного наблюдения. Минимальная численность обследуемых единиц позволяет провести исследование более тщательно и квалифицированно. Например, при переписях населения практикуются выборочные контрольные обходы для проверки правильности записей сплошного наблюдения.

Проведение выборочных исследований статистической информации состоит из следующих этапов:

222

■формулировка объекта и целей выборочного наблюдения;

■обоснование целесообразности выборочного наблюдения;

■отграничение генеральной совокупности;

■выбор схемы отбора единиц для наблюдения;

■определение числа единиц, подлежащих отбору;

■проведение отбора единиц;

■наблюдение отобранных единиц по установленной программе;

■расчет выборочных характеристик и их ошибок;

■распространение выборочных данных на генеральную совокупность;

■анализ полученных результатов.

Конечная задача выборочного наблюдения состоит в том, чтобы распространить полученные в ходе выборочного наблюдения результаты на всю совокупность единиц данного рода, находящихся в сходных условиях (генеральную совокупность).

Отбор единиц из генеральной совокупности в выборку производится таким образом, чтобы выборочная совокупность по своему составу и величине обобщающих статистических характеристик (средних, долей, дисперсий) представляла бы (репрезентировала) генеральную совокупность. Поэтому английские статистики иногда называют выборочный метод репрезентативным (representative method).

Для того чтобы выборка была представительной (репрезентативной), необходимо обеспечить выполнение принципа случайности отбора единиц из генеральной совокупности в выборку. Случайная выборка — это выборка, при которой каждая из единиц генеральной совокупности имеет равную вероятность быть отобранной в выборку.

Невыполнение принципа случайности отбора приводит к тому, что выборка становится непредставительной (нерепрезентативной) как по своему составу, так и по величине обобщающих статисти- ческих характеристик. Следовательно, ее результаты нельзя распространять на генеральную совокупность.

Степень представительности выборки зависит от способа организации выборки и от ее объема. В силу того, что часть (выборка) заведомо не вполне точно представляет целое (генеральную совокупность), полной репрезентативности выборки достичь не удается. Поэтому необходима оценка надежности результатов выборки и воз-

223

можности их распространения на генеральную совокупность. Принцип случайности обеспечивается с помощью различных спо-

собов отбора единиц генеральной совокупности в выборку. Существуют 4 основных способа отбора:

■собственно-случайный (простой случайный);

■механический (систематический);

■серийный (гнездовой);

■типический (стратифицированный, районированный).

На практике могут также использоваться комбинация нескольких способов отбора (комбинированный отбор), отбор в несколько этапов (многоступенчатый отбор), отбор в несколько этапов с сохранением единицы наблюдения (многофазный отбор), комбинирование выборочного и сплошного наблюдения. Выбор схемы отбора зависит от характера изучаемого объекта.

Вне зависимости от способа отбора он может быть повторным и бесповторным. При повторном отборе (схема возвращенного шара) отобранная единица после извлечения из генеральной совокупности регистрируется и вновь возвращается в генеральную совокупность, откуда опять может быть извлечена случайным образом. При бесповторном отборе (схема невозвращенного шара) — отобранная единица в выборку обратно не возвращается.

7.2. Статистическое оценивание

Числовые характеристики генеральной совокупности, как правило, неизвестные, (средняя, дисперсия и др.) называются параметрами (характеристиками) гåнеральной совокупности (обозначают-

ся, например, a , X èëè Xãåí. , σ2ãåí. ). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется

генеральной долей и обозначается р.

По выборочным данным рассчитывают числовые характеристики, которые называют выборочными характеристиками (статисти-

ками) (обозначаются	%	%	,	σ	2	, выборочная доля обозна-
	X , èëè	Xâûá.			âûá.

чается w).

Если из генеральной совокупности объема N извлекается выборка объема n, причем значение признака х1 наблюдается m1 ðàç,

	k
õ2 – m2 ðàç,..., õk — наблюдается mk ðàç, òî ∑mi = n — объем
выборки.	i=1

224

Вместо частот mi каждому значению xi можно сопоставить относительную частоту (частость) wi = mi / n.

Определенным образом заданное соответствие между возможными значениями признака xi и соответствующими им весами (частотами — mi или относительными частотами (частостями) — wi) называют статистическим распределением выборки (вариационным рядом).

Числовые характеристики, получаемые по различным выборкам, как правило, отличаются не только друг от друга, но и от соответствующей характеристики генеральной совокупности. Поэтому числовая характеристика, полученная по выборочным данным, является только статистической оценкой неизвестного параметра генеральной совокупности.

Обозначим И неизвестный параметр генеральной совокупности, И* — его статистическую оценку, полученную по выборочным данным.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Это — требования:

■несмещенности,

■эффективности,

■состоятельности

■достаточности.

Несмещенной называют статистическую оценку И*, математи- ческое ожидание которой равно оцениваемому параметру при любом объеме выборки, т.е. M(И*) = È.

Смещенной называют статистическую оценку И*, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку И*, которая при

n → ∞ стремится к оцениваемому параметру И, т.е. lim P(Θ* −Θ < ε ) = 1.

n→∞

Достаточной называют статистическую оценку, которая содержит всю необходимую информацию об оцениваемом параметре.

Различают точечные и интервальные оценки.

Точечной называют оценку, которая определяется одним числом. В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики.

225

Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова.

Выборочная средняя является точечной несмещенной, состоятельной, а при известном ó — и эффективной оценкой генеральной

средней, т. е. X% âûá. ≈ Xãåí.

Генеральная дисперсия имеет 2 точечные оценки:

σâûá2 . — выборочная дисперсия — смещенная оценка генеральной дисперсии;

S2 — исправленная выборочная дисперсия — несмещенная оценка генеральной дисперсии.

σâûá2

. исчисляется при n ≥ 30 , à S2 — ïðè n < 30.

k

2

mi

%

∑(Xi − Xâûá. )

(7.1)

σâûá2 .

=

i=1

.

n

k

2

mi

%

S2 =

∑(Xi − Xâûá. )

S 2

=

n

σ2

i=1

èëè

âûá..

(7.2)

n −1

n −1

При больших объемах выборки σâûá2 .

è S2

практически совпа-

äàþò.

Генеральное среднее квадратическое отклонение σãåí. также имеет 2 точечные оценки:

σâûá. — выборочное среднее квадратическое отклонение и

S — исправленное выборочное среднее квадратическое отклонение.

σâûá. используется для оценивания σãåí. ïðè n ≥ 30 , à S — äëÿ

оценивания σãåí. , ïðè n < 30.

Ïðè ýòîì: óâûá. = σâûá2 . , à S = S2 .

Интервальной оценкой называют оценку, которая определяется двумя числами — границами интервала, который с заданной на-

226

дежностью накрывает неизвестный параметр генеральной совокупности.

Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом.

Для его определения вычисляется предельная ошибка выборки ∆ , позволяющая установить предельные границы, в которых с заданной вероятностью (надежностью) должен находиться неизвестный оцениваемый параметр генеральной совокупности.

Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изу- чаемой совокупности:

å = È — È*.

(7.3)

Поскольку оцениваются, как правило, средние или доли, то:

ε =	X	− X%	(7.4)
ëèáî
ε = p − w.			(7.5)

Пусть ∆ представляет собой предел, которым ограничена сверху

абсолютная величина		ε		< ∆. Тогда:	Θ −Θ*	< ∆.	Следовательно,
				Θ* − ∆ < Θ < Θ* + ∆.			(7.6)

Мы получили интервальную оценку неизвестного параметра генеральной совокупности.

Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между характеристиками выборочной и генеральной совокупностей будет

сколь угодно мала.
P(		Θ* −Θ		< zµ) > 1 −	1	,	(7.7)
					2
					z
где z — кратность ошибки,

ì— стандартная (средняя) ошибка выборки,

∆= z µ — предельная ошибка выборки.

Согласно центральной предельной теореме Ляпунова выбороч- ные распределения статистик (при n ≥ 30) будут иметь нормальное

227

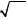
распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:

	P(Θ* − ∆ < Θ < Θ* + ∆) = 2Φ0 (z) = γ ,		(7.8)
z	1	−x2
ãäå Φ0(z) = ∫		e 2 dx — функция Лапласа,
	2π
0

ã — доверительная вероятность (надежность).

Запись показывает, что о величине расхождения между неизвестным параметром генеральной совокупности и его выборочной характеристикой ∆ = z , можно судить лишь с определенной вероятностью, от которой зависит величина z.

Здесь устанавливается связь между пределом ошибки ∆ , гарантируемым с некоторой надежностью ã, кратностью ошибки z и стандартной (средней) ошибкой выборки ì.

Надежность ã устанавливается до проведения выборочного обследования.

Åñëè ã = 0,95, то: со статистической надежностью в 95 % доверительный интервал содержит неизвестный оцениваемый параметр генеральной совокупности. Статистической надежности в 95 % соответствует доверительная вероятность — 0,95. В 5 % случаев утверждение «неизвестный оцениваемый параметр генеральной совокупности принадлежит доверительному интервалу» будет неверным. То есть 5 % задает уровень значимости (α = 0,05) или 0,05 — вероятность ошибки. Доверительная вероятность и уровень значимости дополняют друг друга до 1, т.е. представляют собой сумму вероятностей противоположных событий:

ã + á = 1 .

(7.9)

При n < 30 выборочные распределения статистик будут иметь распределение Стьюдента. Тогда:

					tγ
	P(Θ*	− ∆ < Θ < Θ* + ∆) = 2∫S(t,n)dt = γ ,				(7.10)
					0
ãäå	S(t,n) = B 1	+	t2 −n/2		— плотность распределения Стьюдента,
	n
			n − 1

228

	Bn	=	Γ(n/2)	è
			π(n −1)Γ((n −1)/2)

∞

Γ(x) = ∫tx−1e−tdt — гамма-функция.

0

Значения вероятностей, соответствующие различной кратности ошибки, содержатся в специальных таблицах: при n ≥ 30 — в таблице значений Ф0(z), а при n < 30 — в таблице распределения t- Стьюдента.

При больших выборках, т.е. n ≥ 30 кратность ошибки z определяется по таблицам функции Лапласа из соотношения 2Ф0(z) = ã.

При малых выборках, т. е. n < 30 кратность ошибки z определяется по таблицам Стьюдента по уровню значимости α = 1 – ã и числу степеней свободы k = n – 1.

Стандартная (средняя) ошибка выборки ì представляет собой среднее квадратическое (стандартное) отклонение оценки неизвестного параметра генеральной совокупности ó (È*). В зависимости от оцениваемого параметра и способа отбора стандартная (средняя) ошибка выборки ì определяется по различным формулам.

С помощью доверительного интервала можно оценить генеральную среднюю, генеральную долю и другие неизвестные параметры генеральной совокупности.

Границы доверительного интервала генеральной средней при больших выборках можно оценить с помощью следующего соотношения:

%				%		(z) = γ,		(7.11)
P(X − ∆ < X < X + ∆) = 2Φ0
при малых:
					tγ
%			%		∫S(t,n)dt		= γ .	(7.12)
P(X − ∆ < X < X + ∆) = 2
					0

Границы доверительного интервала генеральной доли при больших выборках можно оценить с помощью следующего соотношения:

	P(w − ∆ < p < w + ∆) = 2Φ0 (z) = γ,		(7.13)
при малых:		tγ
	P(w − ∆ < p < w + ∆) = 2∫S(t,n)dt = γ .		(7.14)
		0

* Далее при больших выборках (n ≥ 30) принимаем ∆ =z, при малых выборках (n > 30) принимаем ∆ = t.

229

Одной из важнейших проблем выборочного метода является определение необходимого объема выборки. От объема выборки зависят надежность оценок параметров генеральной совокупности, размеры стандартной (средней) ì, а, значит, и предельной Д ошибок выборки и экономичность проводимого выборочного наблюдения, так как чем больше объем выборки, тем больше затраты на изучение элементов выборки, но тем меньше при этом ошибки выборки.

Расчет минимально необходимой численности выборки — это ответ на вопрос: «Сколько нужно обследовать единиц генеральной совокупности, чтобы с заранее заданной надежностью г не превысить заранее заданную ошибку Д?». Необходимо помнить, что точ- ность и надежность оценок необходимо задавать до проведения выборки.

Формулы расчета необходимой численности выборки n для различных способов отбора можно получить из формул предельной ошибки ∆ = z и, соответственно, формул стандартных (средних) ошибок выборки.

7.3. Собственно-случайный отбор

Собственно-случайный отбор состоит в отборе единиц из всей генеральной совокупности посредством жеребьевки или на основании таблиц случайных чисел.

Жеребьевка состоит в том, что на каждую единицу отбора составляется карточка, которой присуждается порядковый номер. После тщательного перемешивания по очереди извлекаются карточки, пока не будет отобрано требуемое число единиц.

Случайными числами называются ряды чисел, являющихся реализациями последовательности взаимно независимых и одинаково распределенных случайных величин. Эти последовательности чисел получаются либо с помощью физических генераторов (подбрасыванием кубиков с нанесенными на их сторонами цифрами; вытягиванием из урны карточек с написанными на них цифрами, преобразованием случайных сигналов и использованием др. физико-техниче- ских процессов), либо с помощью программных генераторов (аналитическим методом с помощью программ для ЭВМ).

230