statistika_проц_22

Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин, позволяет представить дисперсию как долю от средней величины.

V = σ 100%			(6.11)
	x

Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя.1

Например, предположим, что стандартное отклонение в выборке валютных счетов в банке «А» и банке «В» равно $20. Данные по банку «А» содержат информацию о счетах, средний размер которых не превышает $100. В банке «В» данные содержат информацию относительно счетов, средний размер которых достигает $1 миллион и больше. В первом случае стандартное отклонение в 20 единиц довольно велико относительно сумм счетов. Для суммы порядка $1 миллиона — что значит вариация плюс-минус $20 относительно среднего? Конечно, такая вариация очень мала. Сравнивая эти два случая, можно сказать, что такая абсолютная мера рассеяния, как среднее квадратическое отклонение, не передает существенной информации при сравнении вариационных рядов. Коэффициент вариации здесь подходит лучше.

Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя. В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.

Однако у такого способа оценки вариации есть и существенный недостаток. Например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением σ = 10 ëåò,

«состарилась» еще на 15 лет. Теперь X = 30 лет, а среднеквадрати- ческое отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15 100 = 66,7 %), со временем оказывается, таким образом, вполне однородной (10/30 100 %= 33,3 %).

1Использование коэффициента вариации имеет смысл при изучении вариации признака, принимающего только положительные значения. Совершенно неправильно пользоваться V в случае измерения колеблемости признака, принимающего как положительные, так и отрицательные значения. Не имеет смысла, например, V, вычисленный для изучения колеблемости среднегодовой температуры воздуха, что особенно ясно при среднегодовой температуре близкой к нулю.

181

Для более ясного представления и использования в экономикостатистическом анализе показатели вариации представлены на рисунке 6.2.

Пример 6.2. Рассмотрим пример расчета средней дневной заработной платы для работников предприятия и показателей вариации рабочих по зарплате.

															Таблица 6.1
Вспомогательная таблица для расчета дисперсии
Заработная	Число				x −				x −		f	(x −		)2		(x −		)2 f
	рабочих,	x	xf			x				x			x				x
плата, руб.	f
Äî 180	5	170	850		73			365				5329				26645
180–200	10	190	1900		53			530				2809				28090
200–220	15	210	3150		33			495				1089				16335
220–240	20	230	4600		13			260				169				3380
240–260	25	250	6250		7			175				49				1225
260–280	20	220	5400		27			540				729				14580
280–300	20	290	5800		47			940				2209				44180
Итого:	115		27950					3305								134435

Решение

Расчет показателей вариации удобнее производить с помощью вспомогательных таблиц, таких как табл. 6.1.

Средняя дневная заработная плата:

∑xf

x = ∑i f = 27950/115 = 243 ðóá.

i

Среднее линейное отклонение:

		∑		xi −		fi
					x			3305
	L =	i					=		= 28,7 ðóá.
				∑ fi				115

i

Следовательно, средняя заработная плата за смену колеблется в пределах от 214,3 до 271,7 руб (Х = 243±28,7).

182

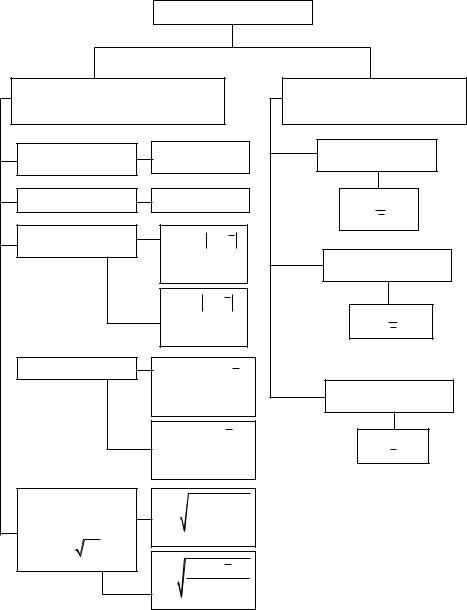
Меры вариации признака

Абсолютные показатели размера вариации, выраженные в единицах измерения признака х

Интерквартильный

размах

Размах вариации

Среднее линейное отклонение

Дисперсия

Среднее

квадратическое

отклонение

σ = σ2

IQR = Q3 −Q1

R = xmax − xmin

L = ∑ x − x n

простое

L = ∑ x − x f

∑ f

взвешенное

σ 2 = ∑(x − x)2

n

простая

σ2 = ∑(x − x)2 f

∑f

взвешенная

	∑(x −		)2
σ =		x
	n
	простое
σ =	∑(x − x)2 f
	∑ f

взвешенное

Относительные показатели интенсивности вариации, выраженные в процентах

Относительный размах вариации

KR = Rx 100

Относительное линейное отклонение

KL = Lx 100

Коэффициент

вариации

V = σ 100 x

Рис. 6.2. Статистическое изучение вариации

183

Дисперсия:

		∑(xi −		)2 fi
			x			134435
	σ2 =	i			=			= 1169 ðóá.2
		∑ fi				115

i

Средний квадрат отклонений заработной платы от ее средней величины составляет 1169 руб. Среднее квадратическое отклонение:

σ = σ2 = 1169 = 34,2.

Средняя дневная заработная плата рабочих колеблется в пределах от 208,8 до 277,2 руб (Х = 243±34,2 руб.).

Коэффициент вариации:

V= σ 100 = 34,2 100 = 14,1 %. x 243

Величина коэффициента вариации небольшая, следовательно, разброс значений заработной платы около ее средней невелик, таким образом, можно сделать вывод, что совокупность однородна по составу, а средняя вполне представительна.

6.3. Меры вариации для сгруппированных данных. Правило сложения дисперсий

Вариация признаков, как правило, обусловлена влиянием различных факторов. Если совокупность разбить на группы по факторному признаку, то это окажет определенное влияние на значение вариации признака в группах. Выявить долю вариации, определяемую теми или иными факторами, можно разделяя всю совокупность на группы по фактору, влияние которого исследуется. Чаще всего для этих целей используются показатели вариации для сгруппированных данных. В этом случае выделяют три вида дисперсий: общую дисперсию; внутригрупповую дисперсию, межгрупповую дисперсию.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов. Внутригрупповая дисперсия измеряет вариацию признака внутри группы, а межгрупповая дисперсия измеряет вариацию групповых средних относительно общей средней.

184

Рассмотрим простейший случай, когда исходная совокупность делится на m однородных групп по одному признаку-фактору.

Допустим, имеется распределение исходной совокупности, представленное в таблице 6.2:

Таблица 6.2

Значение	Число единиц в			j -й группе				Итого
признака x
	1	2		…	m
x1	f1	s1		…	t1	f1 + s1		+ ... + t1	= n1
x2	f2	s2		…	t2	f2	+ s2	+ ... + t2	= n2
…	…	…		…	…			…
xk	fk	sk		…	tk	fk	+ sk	+ ... + tk	= nk
Итого	N1	N2		…	Nm			N

Сначала вычислим m частных средних, то есть среднее значе- ние признака в каждой группе:

k

=

∑ xi fi

i=1

,

x

1

N1

k

=

∑xisi

(6.11)

i=1

,

x

2

N

. . .

2

k

=

∑xiti

i=1

.

x

m

Nm

На основе частных средних x1, x2,..., xm определяем общую среднюю по формуле

xîáù. =

m	k
ãäå N = ∑Nj	= ∑ni .
j−1	i=1

m
∑xjNj	(6.12)
j=1

N

185

Общая дисперсия совокупности

		k
		∑(xi	−		îáù. )2 ni
				x			(6.13)
σîáù2	. =	i=1				.
			N

Общая дисперсия отражает вариацию признака за счет всех условий (факторов), действующих в совокупности.

Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как отклонение групповой средней от общей средней:

	m
	∑(		j	−		îáù. )2 Nj
		x			x
δ 2 =	j=1						.	(6.14)

N

Вариацию внутри каждой группы изучаемой совокупности отражает частная групповая дисперсия, которая исчисляется как сред-

ний квадрат отклонений значений признака x от частной средней xj

k

∑ (xi −

1 )2 fi

x

σ12

=

i=1

.

N1

k

∑(xi −

2 )2 si

x

σ22

=

i=1

(6.15)

N2

…

k

∑(xi −

m )2 ti

x

σm2

=

i=1

.

Nm

В общем виде частную дисперсию запишем так:

k

∑ (xi −

j )2 Nij

x

σj2

=

i=1

,

(6.16)

Nj

ãäå Nij — частоты от i = 1, 2, ...,

k в каждой j-группе.

186

Так как изучаемая совокупность разбита на несколько групп, то для всей совокупности внутригрупповую вариацию будет выражать внутригрупповая дисперсия, которая рассчитывается как средняя арифметическая из групповых дисперсий:

m
∑ σj2Nj		(6.17)
σ 2 = j=1	.

N

Существует закон, связывающий три вида дисперсии.

Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:

			(6.18)
σ2 = δ 2 + σ2 .

Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, формируется из дисперсии, возникающей за счет фактора группировки и дисперсии, возникающей под воздействием всех прочих факторов. Автор этого закона немецкий статистик Вильгельм Лексис (1837–1914).

С помощью закона сложения дисперсий можно оценить удельный вес факторов, лежащих в основе группировки, во всей совокупности факторов, воздействующих на результативный признак. Для этого применяется коэффициент детерминации, который рас- считывается как отношение факторной дисперсии к общей дисперсии результативного признака:

η2 =	δ 2 .	(6.19)
	σ 2

Корень квадратный из коэффициента детерминации называют

эмпирическим корреляционным отношением:

η =	δ 2 .	(6.20)
	σ 2

Эмпирическое корреляционное отношение показывает, какую часть общей колеблемости результативного признака определяет изучаемый фактор, т. е. характеризует влияние группировочного признака на результативный признак. Этот показатель принимает значения в интервале [0,1]. Если связь отсутствует, то η = 0. В этом случае дисперсия групповых средних равна нулю (δ 2 = 0), то есть все групповые средние равны между собой и межгрупповой вари-

187

ации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то η = 1. В этом случае дисперсия групповых средних равна общей дисперсии (δ 2 = σ 2), то есть не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака, а влияние прочих факторных признаков равно нулю. Промежуточные значения η оцениваются по степени их близости к предельным (табл. 6.3).

				Таблица 6.3
	Качественная оценка связи между признаками
	(шкала Чеддока)
η		Связь	η	Связь
0		Отсутствует	0,5–0,7	Заметная
0–0,2		Очень слабая	0,7–0,9	Тесная
0,2–0,3		Слабая	0,9–0,99	Весьма тесная
0,3–0,5		Умеренная	1	Функциональная

Пример 6.3. Рассчитать дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение по данным таблицы.

Решение

Найдем средний размер льгот по трем областям в целом:

				∑		jNj
			îáù. =		x		=	264,3 341,4 + 310,4 235,5 + 490,4 38,9	= 296,2 ðóá.
				j
		x
				∑Nj				615,8

j

Вариация льгот по отдельным областям, обусловленная разли- чием в местах проживания пенсионеров, характеризуется межгрупповой дисперсией:

m

∑(

j

−

îáù. )2 Nj

x

x

2

2

δ2 =

j=1

=

(264,3 − 296,2)

341,5 + (310,4 − 296,2)

235,5

+

615,8

N

+

(490,4 − 296,2)2

= 2976,1.

615,8

188

Таблица 6.4

Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров

â 2004 ãîäó

		Средний размер			Численность	Дисперсия
	Место				пенсионеров,	льгот в области
		денежных льгот
					òûñ. ÷åë.	(группе)
	проживания
		x j			N j	σ2j
	Курская обл.	264,3			341,4	9025
	Курганская обл.	310,4			235,5	2704
	Камчатская обл.	490,4			38,9	2116
	Итого	296,2			615,8	7171,2

Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, обусловленную отдельными факторами, кроме места проживания пенсионеров (например, характером занятости, стажем работы и т.п.):

σ2 = 9025 341,4 + 2704 235,5 + 2116 38,9 = 6171,2. 615,8

Вариация льгот в изучаемых областях России, обусловленная влиянием всех факторов, вместе взятых, определяется общей дисперсией:

σ2 = δ2 + σ2 = 2976,1 + 6171,2 = 9147,3,

отсюда

	η2 =	δ2	=	2976,1	= 0,325.
		σîáù2 .		9147,3

Полученный коэффициент детерминации показывает, что дисперсия льгот зависит от места проживания пенсионеров на 32,5 %. Остальные 67,5 % определяются множеством других неучтенных факторов.

η = η2 = 0,325 = 0,57.

Полученное значение эмпирического корреляционного отношения позволяет утверждать, что существует заметная связь между местом проживания пенсионеров и размером льгот.

189

6.4. Вариация альтернативного признака

При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его отсутствие — 0. Доля вариантов, обладающих изучаемым признаком обозначается р, а доля вариантов, не обладающих признаком, — q. Следовательно, р + q = 1.

Найдем их среднее значение и дисперсию:

=

∑xf

=

1 p +0

q

= p,

x

(6.21)

∑f

p +q

∑(x −

)2 f

(1

− p)2 p + (0 − p)2

q

2

x

2

2

σp

=

∑ f

=

= q

p + p q = pq(p + q) = pq. (6.22)

p + q

Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им.

Если значения 1 и 0 встречаются одинаково часто, то дисперсия достигает своего максимума pq = 0,5 0,5 = 0,25.

Пример 6.4. На 10000 населения приходится 4000 мужчин и 6000 женщин. Определить среднее квадратическое отклонение по полу.

Решение

Доля мужчин в населении p = 4000/10000 = 0,4; доля женщин q = 6000/10000 = 0,6. Тогда дисперсия σp2 = pq = 0,4 0,6 = 0,24 , а среднее квадратическое отклонение σp = σp2 = 0,24 = 0,49 .

Правило сложения дисперсий распространяется и на дисперсии доли признака, то есть доли единиц с определенным признаком в совокупности, разбитой на группы.

Внутригрупповая дисперсия доли определяется по формуле

σ2	= p	(1	− p ).	(6.23)
p	i		i
i

Средняя из внутригрупповых дисперсий рассчитывается так:

		∑ pi (1 − pi )ni =		.
σpi2	=
			pi (1 − pi )		(6.24)
		∑ ni

190