statistika_проц_22

Числа, являющиеся результатами соответствующей вычислительной процедуры, называются псевдослучайными числами. По-следовательность псевдослучайных чисел носит детерминированный характер, но в определенных границах она удовлетворяет свойствам равномерного распределения и свойству слу- чайности.

Существуют специальные таблицы случайных чисел. Числа, содержащиеся в таблице случайных чисел, рассматриваются как порядковые номера единиц генеральной совокупности, подлежащих отбору.

Стандартная (средняя) ошибка выборки для средней определяется как среднее квадратическое отклонение средней величины в генеральной совокупности (средней генеральной)

µx = σ	2	.	(7.15)
	x

Величина средней квадратической (стандартной) ошибки средней арифметической при собственно-случайном повторном отборе может быть определена по формуле

µx	= σX2	,	(7.16)
	n

ãäå σ X2 — дисперсия признака в генеральной совокупности.

Между дисперсиями признака в генеральной и выборочной совокупностях существует следующее соотношение:

σX2 =	n −1	σx2 ,	(7.17)
	n

ãäå σx2 — исправленная выборочная дисперсия признака.

n

Если n достаточно велико, то n −1 близко к единице и диспер-

сию в генеральной совокупности можно заменить на дисперсию в выборке.

Тогда средняя ошибка средней в генеральной совокупности может быть определена как среднее квадратическое отклонение средней величины в выборочной совокупности (средней выборочной).

При бесповторном отборе с каждой отобранной единицей вероятность отбора оставшихся единиц повышается, при этом стандар-

231

тная (средняя) ошибка выборочной средней уменьшается по сравнению с повторным отбором. Ее расчет имеет для собственно-случай- ного бесповторного отбора следующий вид:

µx	= σx2		N − n	.	(7.18)
	n		N −1

При достаточно большом объеме генеральной совокупности N можно воспользоваться формулой

µx	=	σx2			−	n
		n		1			.	(7.19)
						N

Стандартная (средняя) ошибка выборки для доли определяется по формуле

µw = σ	2	.	(7.20)
	p

Величина средней квадратической (стандартной) ошибки доли при собственно-случайном повторном отборе может быть определена по формуле

	µw	=	σp2	,	(7.21)
			n

ãäå σp2 — дисперсия доли в генеральной совокупности (дисперсия

генеральной доли).

Для показателя доли альтернативного признака в выборке (выборочной доли) дисперсия определяется по формуле

σw2	= w(1 − w).		(7.22)
Отсюда	µw	= σw2 .	(7.23)
		n

При бесповторном отборе численность генеральной совокупности сокращается, поэтому дисперсия умножается на коэффициент

N − n	1 −	n	.	(7.24)
N −1
		N

232

Стандартная (средняя) ошибка выборочной доли для собственнослучайного бесповторного отбора имеет следующий вид:

µw	=	σw2	N − n		σw2			−	n
							1			.	(7.25)
		n N − 1			n
									N

Для случая, когда доля (частость) даже приблизительно неизвестна, можно произвести «грубый» расчет средней ошибки выборки для доли, используя в расчете максимальную величину дисперсии доли, равную 0,25.

Тогда, для повторного отбора:

µw	= σw2	<	0,25	=	0,5	=	1	.	(7.26)
			n
	n				n		2 n

для бесповторного отбора:

µw

=

σw2

−

n

<

0,25

−

n

=

1

1 −

n

1

1

.

(7.27)

n

n

2 n

N

N

N

Таблица 7.1

Формулы расчета стандартной (средней) ошибки выборки для собственно-случайного отбора

µ

Собственно-случайный

Собственно-случайный

повторный отбор

бесповторный отбор

Äëÿ

=

σ 2

µx

=

σ 2

−

n

средней

µx

x

x

1

N

n

n

Äëÿ

µw

=

w(1 − w)

µw

=

w(1 − w)

−

n

äîëè

1

n

n

N

Здесь

σx2 — выборочная дисперсия значений признака;

w — выборочная доля, единиц совокупности, обладающих признаком;

n — объем выборки;

N — объем генеральной совокупности;

Nn — доля обследованной совокупности;

233

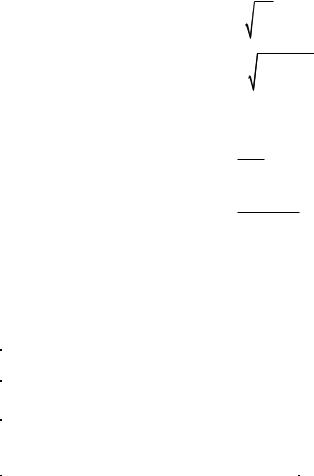
	−	n		— поправка на бесповторность отбора (поправка на ко-
1
		N

нечность совокупности).

Определение необходимого объема выборки n основывается на формулах предельных ошибок выборочной доли и выборочной средней. Например, для повторного отбора предельные ошибки равны

∆x = z	σx2 .			(7.28)
		n
∆w = z		w(1 − w)	.	(7.29)
		n

Отсюда объемы выборок для расчета выборочной средней nx и выборочной доли nw следующие:

= z2σ2 . nx ∆2xx

= z2w(1 − w)

nw ∆2w .

(7.30)

(7.31)

Аналогичным образом определяются объемы выборок при различных способах отбора выборочной совокупности.

Таблица 7.2

Формулы расчета необходимой численности выборки

для собственно-случайного отбора

N

Собственно-случайный

Собственно-случайный

повторный отбор

бесповторный отбор

Для средней

n

=

z 2σ x2

n

=

z 2σ x2 N

x

∆ 2x

x

∆ 2x

N + z 2σ x2

nw =

z 2 w (1 − w )

n

=

z 2 w (1 − w )N

Äëÿ äîëè

w

∆w2 N

+ z 2w (1 − w )

2

∆w

ãäå nx, nw — объемы выборок соответственно для определения ошибок выборочной средней и выборочной доли;

∆x ,∆w — предельные ошибки соответственно выборочной средней и выборочной доли.

234

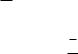
Дисперсия σx2 признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Для приближенной оценки σx2 используются следующие способы:

■дисперсия определяется на основе результатов проведения «пробного» обследования (обычно небольшого объема). По данным нескольких пробных обследований выбирается наибольшее значение дисперсии;

■дисперсия принимается из предыдущих исследований;

■по правилу «трех сигм» общий размах вариации R укладывается в 6 сигм, среднее квадратическое отклонение принима-

ется равным σ = R6 .

■если хотя бы приблизительно известна средняя величина изу- чаемого признака, то σ = x3 ;

■при изучении альтернативного признака (изучении доли), если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, принимается максимально возможная величина дисперсии, равная 0,25.

Âсвязи с тем, что дисперсия оценивается приближенно, рекомендуется рассчитанный объем выборки округлять в большую сторону.

Часто на практике задается не величина абсолютной предель-

ной ошибки ∆x , а величина относительной погрешности ∆относ. , выраженная в процентах к средней величине

∆относ. =

∆x

100 %,

(7.32)

x

откуда

∆

∆x

=

относ.

x

.

(7.33)

100 %

В этом случае объем выборки

nx =

z2σx2

1002.

(7.34)

∆

2

2

относ. (x)

Если известен коэффициент вариации, то объем выборки

nx =

z2V 2

.

(7.35)

∆

2

относ.

235

Для оценки математического ожидания а (генеральной средней)

нормально распределенного количественного признака Х по выбо-

рочной средней % при известном среднем квадратическом откло-

X

нении σ генеральной совокупности (на практике — при большом объеме выборки, т.е. при n ≥ 30) и собственно-случайном повторном отборе:

	%	σ				σ		= 2Ö0 (z) = γ,
					%
P X − z		n	< X < X + z						(7.36)
						n

где z определяется по таблицам функции Лапласа из соотношения

2Ô0(z) = ã;

σ — среднее квадратическое отклонение;

n — объем выборки (число обследованных единиц).

Для оценки математического ожидания а (генеральной средней)

нормально распределенного количественного признака Х по выбо-

рочной средней % при известном среднем квадратическом откло-

X

нении σ генеральной совокупности (при большом объеме выборки, т. е. при n ≥ 30) и собственно-случайном бесповторном отборе:

%

σ

n

σ

n

%

P X − z

1

−

< X < X + z

1−

= 2Ö0(z) = γ.

(7.37)

n

N

n

N

Для оценки математического ожидания а (генеральной средней)

нормально распределенного количественного признака Х по выбо-

рочной средней % при неизвестном среднем квадратическом от-

X

клонении σ генеральной совокупности (на практике — при малом объеме выборки, т. е. при n < 30) и собственно-случайном повторном отборе:

	%	s
					%
P X − t			< X < X + t
		n

s		tγ
		= 2∫S(t,n)dt = γ,
			(7.38)
n		0

где t определяется по таблицам Стьюдента по уровню значимости

α= 1 – ã и числу степеней свободы k = n – 1;

σ— исправленное выборочное среднее квадратическое отклонение;

n — объем выборки.

Для оценки математического ожидания а (генеральной средней)

нормально распределенного количественного признака Х по выбо-

рочной средней % при неизвестном среднем квадратическом от-

X

клонении σ генеральной совокупности (при малом объеме выборки,

236

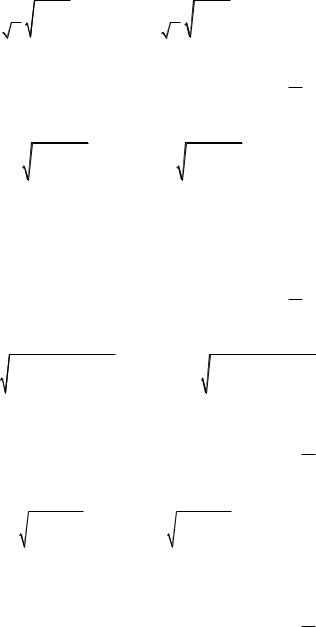
т. е. при n < 30) и собственно-случайном бесповторном отборе:

s

n

s

n

tγ

%

= 2∫S(t,n)dt = γ. (7.39)

%

P X − t

1

−

< X < X + t

1 −

n

N

n

N

0

Для оценки генеральной доли р нормально распределенного ко-

личественного признака по выборочной доле w = m при большом n

объеме выборки, т.е. при n ≥ 30 и собственно-случайном повторном отборе:

	w(1 − w)		w(1 − w)
P w − z		< p < w + z			= 2Ö	(z) = γ,	(7.40)
	n		n		0

где z определяется по таблицам функции Лапласа из соотношения

2Ô0(z) = ã;

w — выборочная доля;

n — объем выборки (число обследованных единиц).

Для оценки генеральной доли р нормально распределенного ко-

личественного признака по выборочной доле w = m при большом n

объеме выборки, т. е. при n ≥ 30 и собственно-случайном бесповторном отборе:

P w − z

w(1 − w)		−	n		< p < w + z
	1
n			N

w(1 − w)		−	n		= 2Ö0(z) = γ.
	1
n
			N

(7.41) Для оценки генеральной доли р нормально распределенного ко-

личественного признака по выборочной доле w = m при малом n

объеме выборки, т. е. при n < 30 и собственно-случайном повторном отборе:

		w(1	− w)			w(1− w)		tγ
								= 2∫S(t,n)dt = γ, (7.42)
	P w − t				< p < w + t
		n − 1				n − 1
								0

где t определяется по таблицам Стьюдента по уровню значимости α = 1 – ã и числу степеней свободы k = n – 1.

Для оценки генеральной доли р нормально распределенного ко-

личественного признака по выборочной доле w = m при малом n

237

объеме выборки, т. е. при n < 30 и собственно-случайном бесповторном отборе:

P w − t

w(1	− w)		−	n		< p < w + t
		1
n				N

	w(1	− w)			n		tγ
				−			= 2∫S(t,n)dt = γ.
			1
	n − 1
					N		0
							(7.43)

Пример 7.1. С помощью собственно-случайного повторного отбора руководство фирмы провело выборочное обследование 900 своих служащих. Средний стаж их работы в фирме равен 8,7 года, а среднее квадратическое (стандартное) отклонение —

2,7 года. Среди обследованных оказалось 270 женщин. Считая стаж работы служащих фирмы распредел¸нным по нормальному закону, определите:

а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих фирмы;

б) с вероятностью 0,90 доверительный интервал, накрывающий неизвестную долю женщин во всем коллективе фирмы.

Решение

По условию выборочное обследование проведено с помощью собственно-случайного повторного отбора. Объем выборки n = 900 единиц, т. е. выборка большая.

а) Найдем границы доверительного интервала среднего стажа работы всего коллектива фирмы, т. е. границы доверительного интервала для генеральной средней.

По условию: % = 8,7; σ = 2,7; n = 900; ã = 0,95.

X

Используем формулу:

%	σ				σ
				%
P(X − z	n	< X < X + z			n	) = 2Φ0	(z) = γ.

Найдем z из соотношения 2Ф0(z) = ã:

2Ô0(z) = 0,95;

Ô0(z) = 0,95 / 2 = 0,475.

По таблице функции Лапласа (приложение 1) найдем, при каком z Ф0(z) = 0,475.

Ô0(1,96) = 0,475. Следовательно, z = 1,96.

238

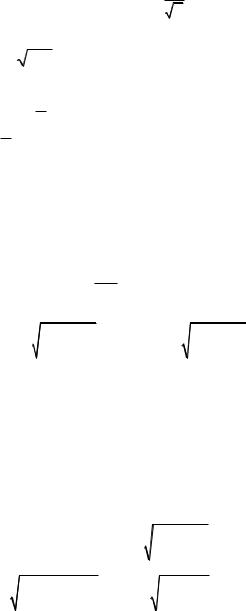
Найдем предельную ошибку выборки:

∆ = z σ ;

x	n

∆		= 1,96	2,7	= 1,96 0,09 = 0,1764;
	x
		900
				X − ∆x	<		< X + ∆x ;
						X
				%			%

8,7 − 0,1764 < X < 8,7 + 0,1764;

8,5236 < X < 8,8764.

С вероятностью 0,95 можно ожидать, что средний стаж работы всего коллектива фирмы находится в интервале от 8,5236 до 8,8764 года.

б) Теперь оценим истинное значение доли женщин во всем коллективе фирмы.

По условию: m = 270; n = 900; ã = 0,9.

Выборочная доля w = 270900 = 0,3. Рассмотрим формулу:

		w(1 − w)		w(1	− w)
	P w − z		< p < w + z				= 2Ö0(z) = γ.
		n		n

Найдем z из соотношения 2Ф0(z) = ã:

2Ô0(z) = 0,9; Ô0(z) = 0,9 / 2 = 0,45.

По таблице функции Лапласа (приложение 1) определим, при

каком z Ф0(z) = 0,45. Ô0(1,64) = 0,45.

Следовательно, z = 1,64.

Предельная ошибка выборки определяется по формуле:

		∆w = z		w(1 − w)		;
					n
∆w = 1,64	0,3 (1 −	0,3)	= 1,64		0,3 0,7			= 1,64 0,0153	= 0,0251;
	900			900

239

w − ∆w < p < w + ∆w; 0,3 −0,0251 < p < 0,3 + 0,0251;

0,2749 < p < 0,3251.

Итак, с вероятностью 0,9 можно ожидать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251.

Ответ. Можно ожидать, что с вероятностью 0,95, средний стаж работы всех служащих фирмы находится в интервале от 8,5236 до 8,8764 года. С вероятностью 0,90 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251.

Пример 7.2. Изменим условие примера 7.1.

а) С помощью собственно-случайного повторного отбора определяется средний стаж работы служащих фирмы. Предполагается, что он подчиняется нормальному закону. Каким должен быть объем выборки, чтобы с доверительной вероятностью 0,95 можно было утверждать, что, принимая полученный средний стаж работы за истинный, соверша-

ется погрешность, не превышающая 0,5 года, если стандартное отклонение σ равно 2,7 года?

б) Каким должен быть объем собственно-случайной повторной выборки, чтобы с надежностью 0,90 можно было утверждать, что максимальное отклонение доли женщин в выборке от доли женщин во всем коллективе фирмы не превышало 0,05, если в прошлом аналогичном обследовании выборочная доля женщин оказалась равной 0,3?

Решение

В данном примере нужно найти необходимую численность выборки. Расчет необходимой численности выборки дает ответ на вопрос: «Сколько нужно обследовать единиц совокупности, чтобы с заранее заданной вероятностью не превысить заранее заданную ошибку?»

à) Äàíî: ∆x = 0,5; σ = 2,7; ã = 0,95.

По условию требуется найти необходимую численность выборки для средней при повторном отборе.

Воспользуемся формулой расчета необходимой численности выборки для средней для собственно-случайного повторного отбора:

n = z2σ2 .

∆x2

240