Электричество и магнетизм (Крахоткин В.И

Если заряды и токи в пространстве распределены непрерывн о, то обе формы уравнений Максвелла эквивалентны. В случае, к огда в среде имеются поверхности разрыва, т.е. поверхности, на ко торых свойства среды изменяются скачкообразно, интегральн ая форма является более общей.

Для стационарных полей (не изменяющихся во времени) уравнения принимают вид:

r	= 0	r	r
rot E		rot H	= j
r		r
div D = ρ		div B = 0,

и в интегральной форме

r	r			r
ò E ×dl = 0			ò D ×dS = òr ×dV
l			S	V
r	r	r		r
òH × dl =		ò j × dS		òB × dS = 0.
l		S		S

В этом случае электрические и магнитные поля оказываются независимыми, что и позволяет изучать отдельно постоянны е электрическое и магнитное поля.

Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем , а переменное электрическое поле всегда связано с порождае мым им магнитным полем, т.е. электрические и магнитные поля нераз рывно связаны друг с другом – они образуют единое электромаг нитное поле.

Теория Максвелла является макроскопической, так как рассматривает поля, создаваемые макроскопическими токами и зарядами. Поэтому эта теория не могла вскрыть внутреннего мех анизма явлений, которые происходят в среде и приводят к возник новению электромагнитного поля. Дальнейшим развитием теор ии Максвелла стала электронная теория Лоренца.

Одним из важнейших выводов теории Максвелла явилось пред - сказание существования электромагнитных волн – изменяю щегося электромагнитного поля, распространяющегося в простр анстве с конечной скоростью.

121

1.10. Электромагнитные волны

Образованиесвободнойэлектромагнитнойволны

Предположим, что в некоторой точке О бесконечной r

непроводящей среды возникает электрическое поле E. Òàê êàê â

среде электрических зарядов, поддерживающих это поле, нет , то r

оно будет исчезать. Но убывающее поле E, согласно теории Макс- r

велла, вызывает появление магнитного поля H. Однако в среде нет

постоянных токов, поддерживающих это поле, и оно будет исч е- r

зать и вызывать появление электрического поля E . Электрическое r 1

ïîëå E уничтожит поле в точке О, но проявится в соседней точ-

1 r

ке 1. Исчезая в точке 1, электрическое поле E вызовет появление r 1

магнитного поля H1, которое будет направлено так же, как и поле r r

H. Поэтому оно уничтожит поле H в точке 1, но проявится вrболее удаленной точке 2. Исчезая, оно вызовет появление поля E2, êî-

торое уничтожит поле в точке 2, но проявится в более удаленн ой r

точке 3 и т.д. Таким образом, вместо первоначального поля E мы получили взаимосвязанные электрическое и магнитное пол я, рас-

пространяющиеся в пространстве, т.е. электромагнитную вол ну. При

r

r

этом векторы E è H взаимно перпендикулярны и перпендикуляр-

r

r

r

r

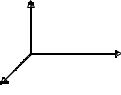
ны скорости распространения волны v. Векторы E,

H è v образу-

ют правовинтовую систему (рис. 52).

r

r Докажем теперь, что векторы E è

r

H удовлетворяют волновому уравнению

E

âèäà

r

∂2ξ

∂2ξ

v

2 = v2

.

10.1

∂t

∂x

2

r

H

Рис. 52. Электромагнитная волна

Так в рассматриваемом случае век- r r

òîðû E è H зависят только от одной координаты и времени, то уравнения Максвелла можно записать в виде:

122

r	r
∂D = −	∂H
∂t	∂x	10.2
r	r
∂B = −	∂E .
∂t	∂x

r

Исключим из уравнений 10.2 напряженность магнитного поля H. Для этого умножим первое уравнение на μμ0, продифференцируем его один раз по времени и получим:

				r			r
mm		× ee		¶2 E	= -mm		¶2 H	.	10.3
				¶t2
	0		0			0 ¶x × ¶t

Второе уравнение продифференцируем один раз по координа те «х»:

r		r
¶2 E		¶2 H
	= -mm0		.	10.4
¶x2		¶x × ¶t

Из равенства правых частей уравнений 10.3 и 10.4 следует, что

r			r
¶2E =	1	×	¶2E .	10.5
¶t2	mm0 × ee0		¶x2

r

Точно такое же уравнение можно получить и для вектора H,

если из уравнений 10.2 исключить напряженность электрическ ого r

ïîëÿ E. Но уравнение 10.5 есть волновое уравнение вида 10.1. Отсюда следует, что электрическое и магнитное поля распрост раняются в пространстве в виде электромагнитной волны. Скорос ть распространения волны в вакууме (μ = 1, σ = 1) равна

c =	1			= 3 ×10		8 ì		,
	e0 ×m0						ñ
а в среде
v =	1	×	1		=		c		.	10.6
	me						me
			e0m0

Можно показать, что в распространяющейся электромагнитной
r	r
волне векторы E è H пропорциональны друг другу, т.е.
	r	r
	ee0 × E =	mm0 × H.	10.7

123

Рис. 54. Вибратор Герца

	r	Из уравнения 10.7 следует,
	E
		r
		векторы E è H одновременно до-
	r	стигают максимума и одновре-
	v	менно обращаются в нуль, т.е.
		колеблются в одинаковой фазе
	r	(ðèñ. 53).

H

Рис. 53. Векторы Е и H в â электромагнитной волне

Экспериментальноеисследование электромагнитныхволн

Свободные электромагнитные волны были впервые получены на опыте Герцем в 1888 году.

Колебательный контур, состоящий из индуктивности L и конденсатора С, не годится для получения электромагнитных во лн, так как электрическое поле сосредоточено между пластина ми конденсатора, а магнитное поле – внутри катушки. В пространст ве, окружающем конденсатор и катушку, полей практически нет, поэтому заметного излучения электромагнитных волн не прои сходит. Чтобы излучение играло заметную роль, нужно сделать облас ти, в

которых возникают поля, менее обособленными от окружающего пространства. Этого можно достигнуть, увеличивая расстояние между обкладками конденсатора и витками катушки. В пределе мы приходим к вибратору Герца, представляющему собой прямолинейный проводник, разделенный искровым

промежутком (рис. 54).

Для возбуждения колебаний вибратор Герца подключается к индуктору (источнику высокого напряжения). Когда напряже ние на искровом промежутке достигало пробойного значения, во зникала искра, которая и замыкала цепь. В результате возникал и свободные колебания, которые продолжались до тех пор, пока ис кра не гасла.

Для приема электромагнитных волн Герц использовал второ й такой же вибратор, т.е. электрический резонанс.

124

На опытах Герц наблюдал отражение, преломление и поляриза - цию электромагнитных волн и определил скорость распрост ранения электромагнитных волн, которая оказалась равной скорост и света.

Энергияэлектромагнитнойволны. ВекторУмова–Пойнтинга

Возможность экспериментального обнаружения электромагнитных волн указывает на то, что эти волны перенося т энергию. Ранее мы показали, что перенос энергии волной мож но характеризовать вектором плотности потока энергии. Он оп ределяется количеством энергии, переносимой волной в единицу времени через единицу площади поверхности, перпендикулярно й к направлению, в котором переносится энергия. Плотность пот ока энергии определяется произведением объемной плотности энергии волны на скорость распространения волны.

Объемная плотность энергии в электромагнитной волне опр е- деляется как сумма объемной плотности энергии электриче ского и магнитного полей:

w = we + wm	= ee0 E2	+ mm0 H2 .	10.8
	2	2

Учитывая выражение 10.7, получим, что объемная плотность энергии электромагнитной волны равна

w = ee0 × mm0 × E × H .

10.9

Умножив уравнение 10.9 на скорость распространения электро - магнитной волны, получим, что плотность потока энергии эл ектромагнитной волны равна

r S = E × H.

10.10

Так как векторы E è H взаимно перпендикулярны и образуют с направлением скорости правовинтовую систему, то направ ление

r r

вектора éëEHùû совпадает с направлением скорости электромагнит-

ной волны. Следовательно, вектор плотности потока энергии электромагнитной волны равен

r r r

S = éëEHùû.

125

r

Вектор S называется вектором Умова – Пойнтинга.

Из теории Максвелла следует, что электромагнитные волны, падающие на некоторую поверхность, должны оказывать на не е давление. В 1900 году П.Н. Лебедев на опыте доказал существование этого давления на твердые тела, а в 1910 году и на газы.

Существование давления электромагнитных волн приводит к выводу о том, что электромагнитному излучению присущ опре деленный импульс, определяемый выражением

r = W , p

c

где W – энергия электромагнитной волны.

1.11.Гармонический осциллятор (электрические системы)

Свободныеэлектромагнитныеколебания. ФормулаТомсона

В механике мы рассматривали систему (груз, подвешенный к пружине), способную совершать гармонические кол е- бания. Когда груз находится в крайних положениях, его кине ти- ческая энергия равна нулю, а потенциальная энергия максим альна. При прохождении грузом положения равновесия, напротив , кинетическая энергия максимальна, а потенциальная энерг ия равна нулю. Поэтому можно сказать, что механическое колебание е сть периодическое превращение энергии системы из кинетичес кой в потенциальную и наоборот.

Аналогичные процессы мы имеем и при электромагнитных колебаниях. Электромагнитные колебания, как и механические , могут возникать только в определенных системах. Простейшей системой, в которой могут возникать электромагнитные колебани я, является колебательный контур. Колебательный контур – это электрическая цепь, состоящая из последовательно соединенны х катушки индуктивности L, конденсатора С и активного сопроти вле-

126

Рис. 55. Колебательный контур

C

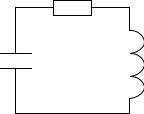
ния R (рис. 55). Различают линейные R и нелинейные контуры. В линейных контурах его параметры L, C, R не зависят от интенсивности колебаний,

Lи период колебаний не зависит от

амплитуды (изохронность колебаний). В нелинейных контурах, например при наличии катушки с ферромагнитным сердечником, изохронность не соблюдается.

Если при разомкнутой цепи зарядить конденсатор, то он буд ет

	æ	q2	ö
	обладать энергией ç W =		÷. При замыкании заряженного конден-
		2C
	è		ø

сатора на катушку индуктивности в цепи возникает электри ческий ток, и заряд конденсатора начинает уменьшаться. Через четверть периода заряд конденсатора станет равным нулю, но сила то ка в цепи достигает максимального значения, и магнитное поле в ка-

æ	LI2 ö
тушке будет обладать энергией ç W =		÷	. Затем ток в цепи начнет
è	2 ø

уменьшаться, но возникающая при этом ЭДС самоиндукции буд ет поддерживать уменьшающийся ток, что приводит к перезаряд ке

	æ	q2	ö
	конденсатора и образованию энергии электрического поля ç W =		÷.
		2C
	è		ø

Если сопротивление контура R равно нулю (идеальный контур), то указанный процесс периодического превращения эн ергии

		æ	q2 ö
	электрического поля	ç W =			в энергию магнитного поля
			2C ø
		è

æ	LI2 ö
ç W =		÷	и обратно будет продолжаться неограниченно долго и
è	2 ø
мы получим незатухающие электромагнитные колебания.

Из сопоставления электромагнитных и механических колеб а-

	æ	q2 ö
	ний следует, что энергия электрического поля ç W =			анало-
		2C ø
	è

127

æ kx		2	ö
гична потенциальной энергии ç				, а энергия магнитного поля
	2		ø
è

æ	LI2 ö			æ mv2		ö
ç W =		÷	аналогична кинетической энергии	ç		÷. Èç ýòîé
è	2 ø			è	2	ø

аналогии следует, что индуктивность L играет роль массы m, вели-

чина, обратная емкости 1 , играет роль коэффициента жесткости k,

C

	заряду q соответствует смещение х, сила тока I =	dq	, скорость v =	dx	.
		dt
				dt

Докажем, что эта аналогия распространяется и на описывающие их уравнения.

Так как сопротивление контура равно нулю, то закон Ома для неоднородного участка цепи запишется в виде

ϕ1 − ϕ2 + E = 0.	11.1
Учитывая, что

j1 - j2 = -U = -

q

,

E = -L

dI

,

11.2

dt

C

получим

q

+ L

dI

= 0.

11.3

C

dt

Разделив выражение 11.3 на L и учитывая, что

dI

= q¢¢, ïîëó-

dt

чим уравнение

q¢¢ +

1

q = 0.

11.4

LC

Если ввести обозначение

w02

=

1

,

11.5

LC

уравнение 11.4 примет вид

q¢¢ + w02 × q = 0.

11.6

128

Уравнение 11.5 аналогично уравнению, описывающему механические колебания груза на пружине. Решением этого однор одного дифференциального уравнения является функция

q = q0 ×cos(w0 t + a).

11.7

Таким образом, заряд на обкладках конденсатора изменяетс я по гармоническому закону с частотой, определяемой выраже нием 11.5. Эта частота называется собственной частотой колебаний контура. Для периода колебаний в колебательном контуре по луча- ется формула

T = 2p LC,

11.8

называемая формулой Томсона.

Свободныезатухающиеколебания

Всякий реальный колебательный контур обладает сопротивлением. Это приводит к тому, что часть энергии, запас енная в контуре, теряется на нагревание проводников, поэтом у свободные колебания являются затухающими. Закон Ома для неод нородного участка цепи в этом случае будет иметь вид

IR = −

q

− L

dI

.

11.9

C

dt

Разделив выражение 11.9 на L и заменив I =

dq

è

dI

= q¢¢,

dt

получим уравнение

dt

q¢¢ +

R

× q¢ +

1

× q = 0.

11.10

L

LC

Учтя формулу 11.5 и введя обозначение

b =

R

,

11.11

2L

уравнению 11.10 можно придать вид

q¢¢ + 2bq¢ + w02q = 0.

11.12

При условии, что b2 << w02, решение этого уравнения имеет вид
	q = q0 × e−βt × cos (wt + a),	11.13
ãäå ω = ω2	− β2 .
0

129

õ
õ1	õ2
	t
Рис. 56. Затухающие колебания

Выражение 11.13 описывает гармонические колебания с частотой ω, амплитуда которых не остается постоянной, а уменьшается с течением времени по экспоненциальному закону (рис. 56). Показатель β называется коэффициентом затухания.

Найдем промежуток времени τ, в течение которого амплитуда колебаний уменьшается в «е» раз.

−βt

q0e ( ) = e èëè eβτ = e.

q0e−β t +τ

Отсюда следует, что b = 1t, т.е. коэффициент затухания равен

величине, обратной промежутку времени τ, в течение которого амплитуда колебаний уменьшается в «е» раз. Этот промежуто к времени получил название времени релаксации.

Затухание колебаний принято характеризовать логарифмич еским декрементом затухания λ. Логарифмическим декрементом затухания называется натуральный логарифм отношения двух соседних амплитуд, отстоящих друг от друга на один период (рис. 56):

−βt

λ = ln q0e ( ) = βT. 11.14

q0 e−β t +T

Легко показать, что логарифмический декремент затухания λ обратен по величине числу колебаний Ne, совершаемых за время τ, в течение которого амплитуда колебаний уменьшается в «е» раз:

1			1		1
l = bT =		× T =		=		.	11.15
	t		t		Ne

T

Гораздо чаще качество колебательного контура характери зуют его добротностью Q, которая определяется по формуле

Q = p	11.16
l

130