Электричество и магнетизм (Крахоткин В.И

E

Рис. 6. К доказательству теоремы Гаусса

поверхность. Она была установлена М. В. Остроградским в виде некоторой общей математической теоремы и Гауссом – применительно к случаю электри- ческого поля. Докажем теорему вначале для точечного заряда q.

Окружим точечный заряд сферой радиусом R (рис. 6) и тогда для потока вектора напряженности, с учетом формул 1.7 и 1.5, получим

F =

ò

E ×dS = E

ò

dS = E ×S =

1

×

q

× 4pR 2

=

q

.

1.8

4pe0

R

2

e0

S

S

Полученный результат будет справедлив и для любой другой замкнутой поверхности. Если поверхность не охватывает за рядов, то Ф = 0. В этом случае линии напряженности и входят, и выходят из поверхности.

В общем случае, когда замкнутая поверхность охватывает N электрических зарядов,

					N
N	N	q	i		åqi
F = åFi	= å			=	i=1	.	1.9
		e0
i=1	i=1				e0

Формула 1.9 выражает теорему Гаусса – поток вектора напряженности электрического поля через любую замкнутую пове рхность равен алгебраической сумме зарядов, охватываемых этой по верхностью, деленной на электрическую постоянную.

Используя теорему Гаусса можно рассчитать напряженност ь электрического поля во многих случаях. Рассмотрим некоторые примеры.

Равномерно заряженная плоскость

Пусть имеется бесконечная плоскость, равномерно за-

ряженная с поверхностной плотностью заряда s. Очевидно, что r

вектор напряженности E в этом случае, будет перпендикулярен плоскости Eτ. В противном случае появится составляющая вектора напряженности (рис. 7б), направленная параллельно плоскост и и

11

	E
		E

Å

àá

Рис. 7. Поле равномерно заряженной плоскости.

приводящая к изменению распределения заряда на плоскости, что противоречит условию.

В этом случае в качестве замкнутой поверхности удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограни- ченный двумя плоскими основаниями, перпендикулярными к линиям напряженности и расположенными

по обе стороны плоскости (рис. 7а).

Так как вектор напряженности не пронизывает боковой пове рх-

ности цилиндра, то F = 2 × E ×S, но по теореме Гаусса F = q = s ×S.
e0	e0

Из равенства правых частей этих выражений следует, что ра вномерно заряженная плоскость создает однородное электрич еское поле с напряженностью

E =	s
	2e0 .	1.10

Поле у поверхности заряженного проводника

Учитывая, что вектор напряженности поля перпендикулярен поверхности проводника (рис. 8) и поле внутри прово д- ника отсутствует, можно получить

E = σ ε0

E

Рис. 8. Поле у поверхности проводника

r r
èëè s = e0 E = D.	1.11

Величина D получила название электрического смещения, так как у поверхности заряженного проводника она равна поверхностной плотности заряда σ, т.е. величине заряда, сместившегося внутри проводника, на единице площади поверхности.

12

Как видно из полученного выражения, напряженность электрического поля в этом случае не зависит от формы проводни ка и распределения зарядов на нем.

Поле двух заряженных пластин

Рассмотрим электрическое поле, создаваемое двумя равномерно заряженными пластинами. При появлении на одной из пластин заряда с поверхностной плотностью +σ на второй пластине появляется заряд противоположного знака с поверхност ной плотностью –σ (рис. 9). Эти заряды под действием силы взаимного притяжения будут сосредоточены на внутренних поверхнос тях пластин. Заряженные плоскости каждой пластины создают по обе стороны от себя электрическое поле с напряженностью, выражае мой

формулой E =	s	. Вне пластин эти напряженности направлены
	2e ×e0

в разные стороны и их сумма равна нулю (рис. 9). Между пластин а- ми, напротив, эти поля направлены в одну сторону и, складываясь, дают

s
E = e ×e0 .	1.12

	Ðèñ. 9. Ïîëå äâóõ	Поле равномерно заряженной нити
	заряженных плоскостей
		Рассмотрим электрическое поле,
		создаваемое равномерно заряженной

с линейной плотностью заряда τ нитью. В качестве замкнутой поверхности в этом случае удобно взять цилиндрическую по - верхность, ось которой совпадает с нитью (рис. 10). Очевидно,

		что и в этом случае вектор напря-
E		женности перпендикулярен нити и
		будет пронизывать боковую поверх-
		ность цилиндра. Следовательно, по-
	òîê			вектора напряженности
		F = E × 2pr × l, но по теореме Гаусса
		F =	q	= t × l. Из равенства правых ча-
			e0	e0

Рис. 10. Поле равномерно стей этих выражений следует, что назаряженной нити пряженность электрического поля

13

равномерно заряженной нити определяется выражением

E =	1		t	.	1.13
2pe0			e × r

Работапоперемещениюзарядавполе. Потенциал.Разностьпотенциалов

		F
		Ñ
Â	dr	dS
	r1	r2

q0

Рис. 11. К определению работы поля по перемещению заряда

Найдем работу электрического поля, создаваемого то- чечным электрическим зарядом q0, при перемещении заряда q из точ- ки В в точку С (рис. 11). По определению работа на малом участке пути определяется по формуле

dA = F × dS × cos a. Учитывая, что

dS × cos a = dr è F = k qq0 , ïîëó- r2

чим для элементарной работы

dA = k qq0 dr. Интегрируя полу- r2

ченное выражение, будем иметь

r2	qq					æ	1	1		ö
A = òk		0
			dr = -kqq0			ç		-		÷.	1.14
	r2						r		r
r1						è	2	1		ø
Введем функцию
	j = k			q0	+ C .						1.15
				r

Функция ϕ, определяемая выражением 1.15, называется потенциалом электрического поля в данной точке. С учетом формулы

1.15 выражение 1.14 примет вид
A = -q (j2 - j1 ) .	1.16

Величину (ϕ2 − ϕ1 ) = Δϕ называют разностью потенциалов

между двумя точками электрического поля. Из уравнения 1.16 следует, что разность потенциалов численно равна работе с ил

14

Рис. 12. К устройству электрометра

поля при перемещении единичного положительного заряда м ежду этими точками поля.

Понятие разности потенциалов широко используют по двум причинам.

Во-первых, описание электрического поля при помощи потенциала гораздо проще, чем при помощи напряженности поля. На - пряженность поля – вектор, в то время как потенциал есть ск аляр

èвполне определен в каждой точке одной величиной – своим численным значением.

Во-вторых, разность потенциалов гораздо проще измерить на опыте, чем напряженность поля. Для измерения напряженност и электрического поля нет удобных методов, в то же время сущ е- ствуют многочисленные методы измерения разности потенц иалов

èразнообразные приборы.

Разность потенциалов достаточно просто измерить на опыт е. Для этого служат приборы, называемые электрометрами, или электростатическими вольтметрами.

Простейший электрометр содержит легкую стрелку, укрепле нную на металлическом стержне. Стрелка может поворачиваться в округ горизонтальной оси. Стержень со стрелкой помещают внутрь ме талли- ческого корпуса, чтобы защитить от влияния внешних электр ических полей, и хорошо изолируют от него (рис. 12). Прибор имеет шкалу, позволяющую отсчитывать угол отклонения стрелки прибор а.

Для измерения разности потенциалов (напряжения) между Зе м- лей и заряженным проводником корпус прибора заземляют, а стержень соединяют с заряженным телом.

Легко показать, что отклонение стрелки электрометра будет зависеть только от напряжения, существующего между стрелкой и корпусом. Так как электрометр имеет металлический корпус, то электрическое поле, возникающее в нем, будет зависеть только от напряжения, приложенного к электрометру. В электрическом поле на стрелку будут действовать силы, приводящие к ее отклонению от вертикали. Прибор можно проградуировать, т.е. определить, каким напряжениям соответствуют различные углы отклонения стрелки.

15

Данный электрометр очень удобен для измерения высоких
(104 −106 B) напряжений, а для измерения малых разностей по-
тенциалов применяются другие методы.
Выбор произвольной постоянной С в выражении 1.15 может
быть произвольным. Простейший случай мы получим, если пол о-
жим С = 0, тогда потенциал точки, удаленной в бесконечность,
будет равен нулю. В этом случае
ϕ = k q = A .		1.17
r	q
Потенциал данной точки электрического поля численно рав ен
работе, которую совершают силы поля при перемещении полож и-
тельного единичного заряда из бесконечности в данную точ ку поля.
На практике оказалось удобнее считать потенциал земной п о-
верхности равным нулю.
Потенциал электростатического поля представляет собой функ-
цию, меняющуюся от точки к точке. Однако во всяком реальном
случае можно выделить совокупность точек, имеющих одинак о-
вый потенциал.
Геометрическое место точек, имеющих одинаковый потенциа л,
называется поверхностью равного потенциала, или эквипот енци-
альной поверхностью.
Электрическое поле можно изображать не только с помощью
линий напряженности, но и с помощью эквипотенциальных по-
	верхностей. При этом нужно
	иметь в виду, что линии напря-
	женности всегда перпендикуляр-
	ны эквипотенциальным поверх-
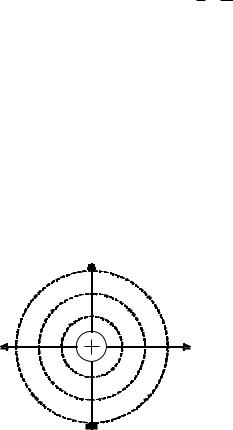
	ностям. В случае	точечного
	заряда эквипотенциальные по-
	верхности представляют собой
	сферы с центром, совпадающим
	с точечным зарядом (пунктирные
	линии на рисунке 13).
	Из выражения 1.16 следует,
	что работа сил электрического
Рис. 13. Линии напряженности	поля не зависит от формы и дли-
и эквипотенциальные поверхности	ны пути, но определяется началь-
точечного заряда.

16

ным и конечным положением заряда в поле. Работа сил электр и-

ческого поля на замкнутом пути (j1 = j2 ) равна нулю. Следовательно, электрическое поле является потенциальным, а элек три- ческие силы – консервативными.

Ранее мы показали, что работа консервативных сил равна из - менению потенциальной энергии, взятой с противоположным зна-

êîì: A = -(W2 - W1 ). Поскольку в бесконечности	W1 = 0, òî
A = -W2 = -qj
. Следовательно, потенциальная энергия заряда в
поле определяется по формуле
W = q ×j.	1.18

Из данного выражения следует, что потенциал – энергетическая характеристика поля.

Напряженностьэлектрическогополя какградиентпотенциала

Установим теперь связь между напряженностью поля и потенциалом. Существование такой связи следует из того факта, что работа электрических сил, выражаемая через напряженн ость, может быть выражена и через разность потенциалов.

Найдем работу по перемещению заряда в направлении оси Х. С одной стороны, dA = EX × dx × q, но с другой – dA = -q × dj . Îò-

сюда следует, что EX = -

dj

. Рассуждая аналогично, можно полу-

dx

÷èòü, ÷òî EY

= -

dj

, EZ

= -

dj

. Тогда в общем случае будем иметь

dy

dz

r

æ

¶j r

+

¶j r

¶j r ö

= -gradj = -Ñj.

1.19

E = -ç

i

j +

k ÷

è

¶x

¶y

¶z ø

Напряженность электрического поля равна градиенту поте нциала, взятому с противоположным знаком. Знак минус говорит о том, что напряженность поля всегда направлена в сторону у бывания потенциала.

17

Для однородного электрического поля выражение 1.19 принимает вид

E = − Δϕ,

1.20

d

где d – расстояние между двумя точками, Δϕ – разность потенциалов между ними.

Для поля со сферической или цилиндрической симметрией вы -

ражение 1.19 имеет вид
E = -	dj	.	1.21
	dr

Циркуляциявекторанапряженности электрическогополя позамкнутомуконтуру

Если в качестве заряда, переносимого в поле, взять положительный единичный заряд, то работу по его перемещен ию

на пути dl можно найти по формуле: dA = F × dl × cos α, íî â ýòîì
r r	r	r
случае F = E,	dl cos a = d l и, следовательно, dA = E × d l. Äëÿ îïðå-

деления работы на замкнутом пути это выражение необходим о

r r	r r
проинтегрировать: A = òE × d l . Выражение òE × d l называется цир-
1	1

куляцией вектора напряженности электрического поля. Ран ее мы показали, что работа сил электрического поля на замкнутом пути равна нулю, значит

r
òE × dl = 0.	1.22

1

Равенство нулю этого интеграла говорит о том, что в природ е существуют два вида электрических зарядов, являющихся ис токами и стоками электрического поля.

18

1.2.Электрическое поле в среде. Поляризация диэлектриков

Электрическийдиполь.

Дипольводнородноминеоднородномполе

Рассмотрим два точечных заряда величиной +q и –q, жестко связанных между собой и смещенных на расстояние l друг от друга. Такую пару зарядов называютrэлектрическим дипол ем.

		l	Вектор l , направленный по оси ди-
			поля от отрицательного заряда к поло-
	p
			жительному и равный расстоянию меж-
			ду зарядами, называется плечом дипо-
			ля. Вектор		r
				r
					× l	2.1
		Рис. 14. К определению		p = q
		электрического диполя	называется дипольным моментом, или
			электрическим моментом диполя (рис. 14).
			r	Во внешнем однородном
				электрическом поле на ди-
	à)		F
		a		поль будет действовать мо-
			r			r
				ìåíò ïàðû ñèë F (ðèñ. 15à)
			E
	r			M = F × l ×sin a =
	F			= q × E × l ×sin a = p × E ×sin a.
	á)
				Очевидно, что M = 0 при
	r		r
	F			, т.е. в однородном
			F	sin a = 0
				электрическом поле диполь
				ориентируется так, что его ди-
		Рис. 15. Диполь в однородном		польный момент направлен
		электрическом поле		вдоль вектора напряженности
				поля (рис. 15б). Рассмотрим,

как будет себя вести диполь в неоднородном поле. В этом слу чае диполь будет обладать потенциальной энергией W = q(j+ - j− ).

Òàê êàê (j	- j	) =	dj		×l ×cosa è	dj	= -E, то для потенциаль-
+	−		dx			dx

ной энергии получим выражение W = -p × E × cos a . Ранее мы по-

19

казали, что Fx = - dW, значит, на диполь в этом случае будет dx

действовать сила F	= p ×	dE	×cos a. Ïðè a < p диполь будет втяги-
x		dx		2
ваться в поле (F > 0) è ïðè a > p				– выталкиваться из поля (F < 0).
x	2			x

Видыдиэлектриков

Диэлектрики (как и всякое вещество) состоят из атомов и молекул. Положительный заряд сосредоточен в ядрах а томов и молекул, а отрицательный – в электронных оболочках атом ов. Так как положительный заряд всех ядер молекулы равен сумм арному заряду электронов, то молекула в целом нейтральна и е е можно рассматривать как электрический диполь с дипольны м моментом, определяемым по формуле 2.1.

Первую группу диэлектриков (азот, водород, кислород и др.)

составляют вещества, молекулы которых имеют симметрично е стро- r

ение, следовательно, дипольный момент pi такой молекулы равен

нулю. Молекулы таких диэлектриков называются неполярным и. r

Во внешнем электрическом поле с напряженностью E заряды неполярных молекул смещаются в разные стороны (деформацион ная или электронная поляризация) и диэлектрик приобретает ди польный момент

r	= n ×b × e0 × V × E ,	2.2
pV

ãäå β – коэффициент пропорциональности, называемый поляризуемостью молекулы и зависящий от строения молекулы, ε0 – электрическая постоянная, V – объем диэлектрика.

Вторую группу диэлектриков (вода, окись углерода, метан) образуют вещества, молекулы которых имеют асимметричное стро-

ение, значит, молекулы их обладают дипольным моментом r ¹ . pi 0

Молекулы таких диэлектриков называют полярными. В отсутс твие внешнего электрического поля, вследствие хаотического т еплового движения, дипольные моменты молекул ориентированы хао ти- чески и результирующий дипольный момент равен нулю. Если такой диэлектрик поместить во внешнее электрическое пол е, то

20