Physics of biomolecules and cells

R.F. Bruinsma: Physics of Protein-DNA Interaction

57

as −e/b, with b the spacing per elementary charge, then the surface charge density σ equals −e/2πab. The charged rod is immersed in a cylindrical container with radius R a filled with water (you also could consider R as the typical distance to other rod-like macro-ions).

4.2.1 The primitive model: Ion-free

We start with the case of ion-free water. Poisson’s Law reduced to Laplace’s equation ∆φ = 0 in a cylindrical geometry with solution φ(r) = α ln r + β. Imposing the boundary condition equation (4.2) gives α:

φ(r) = −	2λ	ln r/R	(4.8)
	ε

(demanding φ(R) = 0). The first thing you learn from equation (4.8) is that there is a characteristic voltage scale ∆V = −λ/ε in the problem. How does this voltage scale compare with the thermal energy? First, introduce

the Bjerrum Length lB:

e2
	= kBT.	(4.9)
εlB

Two monovalent ions that are one Bjerrum length apart have an electrostatic energy equal to the thermal energy (the Bjerrum length is about 7 ˚A under standard conditions). In terms of the Bjerrum Length, the ratio ξ = e∆V /kT of the electrostatic and thermal energies equals:

ξ =	e∆V	=	lB	·	(4.10)
	kBT		b

For DNA, this ratio – which is known as the Manning Parameter – is about 5, so the electrostatic energy dominates over the thermal energy near the surface of DNA.

4.2.2 The primitive model: DH regime

Now let’s add ions and assume the high temperature limit where we can apply DH theory. We must solve the Helmholtz Equation ∆φ = κ2φ in cylindrical geometry. The appropriate solution vanishing at infinity is the K0 Bessel Function: φ(r) = αK0(κr). Using the boundary condition

equation (4.2) to fix the intgeration constant α gives α = 2λ so

εκaK0(κa)

φ(r) =	2λ			(κr).	(4.11)
			K0
	εκaK	(κa)
	0

58	Physics of Bio-Molecules and Cells

For small arguments, K0(x) can be approximated by − ln x, and we recover the ion-free case (up to a constant). For large arguments, K0(x) can be approximated by x−1/2 exp −x, so the potential is screened exponentially distances large compared to the Debye screening length. From the relation ρ = −εκ4π2 φ it follows that there is a cloud of positive ions surrounding the negatively charged rod (also called the “bilayer”). The total the charge per unit length of this cloud equals:

λ+ = −	εκ2	R	2πrd r	2λ		(κr) = −λ.	(4.12)
					K0
	4π	a		εκaK0(κa)

The positive charge per unit length of the bilayer is just equal to the negative charge per unit length so the net enclosed charge is zero. You thus can consider the charged rod as a cylindrical capacitor.

The number of positive and negative small ions is thus not equal. The extra (positive) ions required to neutralize the rod are called the “counterions”, the other positive and negative ions the “co-ions”.

4.3 Manning condensation

4.3.1 Charge renormalization

Is DH theory valid for DNA under physiological conditions? It depends. For DNA, κa is of the order of one, so it follows from equation (4.11) that the characteristic voltage scale at the surface is still ∆V = −λ/ε. We know that in that case the ratio ξ of the electrostatic energy and thermal energy is large compared to one so DH theory fails seriously near the surface of DNA. Yet, far from the surface the potential decreases to zero. In the asymptotic regime far from the macro-ion where the electrostatic energy is small compared to the thermal energy, the DH equation must be valid. What this really amounts to is that when we solve the DH equation, we are

not allowed to use the boundary condition equation (4.2) to determine α!

The integration constant α must be determined by a full solution of the non-linear Boltzmann–Poisson (BP) equation (or even some more accurate theory). This leads to a change in the value of α which we will incorporate by the introduction of a “renormalized” charge per unit length λ :

	lim φ(r) =		2λ		K0(κr).	(4.13)
			εκaK	(κa)
	r	→∞
			0

We thus can use the nice, linear DH theory to compute, for example, the asymptotic force of interaction between two highly charged rods, for separations large compared to the Debye screening length, provided we replace everywhere the bare charge by the renormalized charge. All the “hard” part

R.F. Bruinsma: Physics of Protein-DNA Interaction

59

of the problem is hidden in obtaining the renormalized charge, but that can be determined experimentally if necessary! We can use in general DH theory to study the phase behavior of dilute solutions of macro-ions of the same sign of charge and it has been used with success to study dilute polyelectrolyte and colloidal solutions. It is however not appropriate for a study of the short-range interaction between macro-ions. The interaction between DNA strands in chromatin and the interaction between macro-ions of opposite charge, such as in DNA/protein association, are beyond DH theory as we shall see shortly. Our next step is to look for a physical description that can apply to these cases without excessive mathematical complications.

4.3.2 Primitive model: Oosawa theory

First, let’s try to estimate the renormalized line charge. Assume that the Manning Parameter is large compared to one so the electrostatic energy of an ion near the surface of the negatively charged rod exceeds kBT . Some of the positive ions will be attracted by the negative charges of the rod and establish a close association with the rod. For the first of these “condensed” ions, the thermal energy is small compared to the electrostatic energy so thermal fluctuations will not break up the association. The condensed ions are known as the “Manning Cloud” [47] by the way. Condensed ions are restricted to a thin sheet surrounding the rod and should be considered as a separate “population” from the free ions further out in the Debye Cloud (see Fig. 29).

As more and more positive ions become associated with the rod, the e ective charge per unit length decreases and the ratio of electrostatic and thermal energy decreases as well. We will estimate the equilibrium value λ of the e ective charge by demanding that the ions of the two populations are in chemical equilibrium with each other. Note that ions can freely exchange between the two populations. This point of equilibrium is set by the condition that the electrostatic energy per ion in the Manning Cloud must be comparable to thermal energy: the energy gain per ion is then balanced by the entropy loss. Using equation (4.10), this condition gives

e∆V ≈ −λ e/ε ≈ 1, or λ ≈ −e/lB. The prediction is thus that the renor-

kBT kBT

malized charge per unit length should be of order one charge per Bjerrum Length. That is curious: the renormalized charge should not depend on the bare charge! Of course, if the bare charge per unit length is so small that the Manning parameter is less than one, then there would be no charge renormalization in the first place and λ = λ.

We can make this argument more precise in the limit κa 1. Let CC be the ion concentration of the condensed fraction and CDH the free ion concentration far from the rod but inside the DH cloud. If you placed a microscopic voltmeter with one electrode at the edge of the Debye layer and

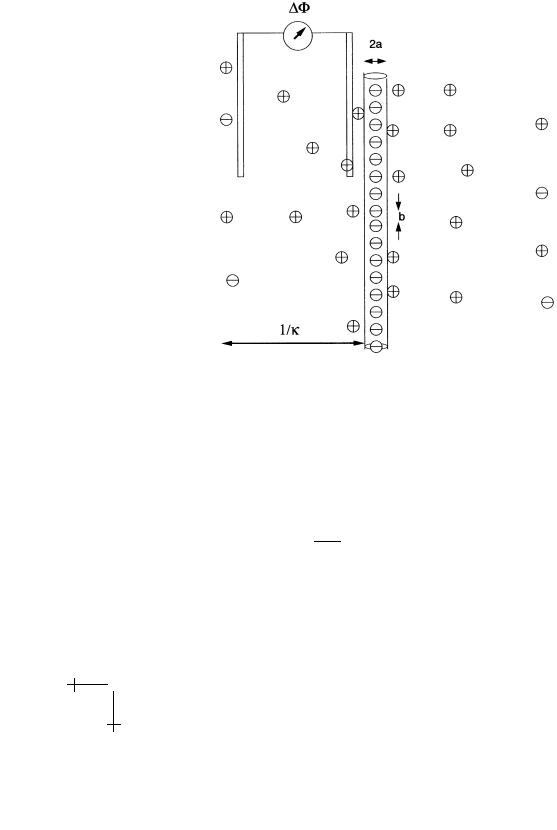
60	Physics of Bio-Molecules and Cells

the other just inside the Manning cloud, you would measure an electrical voltage di erence ∆Φ between the two populations:

Fig. 29. Measuring the potential of the primitive model.

We can use the DH expression equation (4.12) for the asymptotic part of the electrostatic potential to compute ∆Φ:

∆Φ = −(2λ /ε) ln(1/κa).

(4.14)

Since the two populations are in chemical equilibrium with each other, their concentration ratio must obey the Boltzmann Distribution:

CC	= exp(−e∆Φ/kBT ).	(4.15)
CDH

Next, we know from DH theory (Eq. (4.12)) that the free ion concentration of the Debye cloud must cancel the e ective charge of the rod:

eπκ−2CDH ≈ −λ .

(4.16)

R.F. Bruinsma: Physics of Protein-DNA Interaction

61

Overall charge neutrality requires that the total number of free ions per unit length in the Debye cloud plus that of the condensed ions must cancel the bare charge per unit length:

eCCπa2 + eCCπκ−2 = −λ.

(4.17)

Now eliminate the free and condensed ion concentrations in the Boltzmann condition using the last two equations. Inserting equation (4.13), you then obtain a self-consistency condition for the renormalized charge λ :

| |	|λ |	|		=		− εkBT|
λ	− |λ		(κa)2		exp		2e|λ		ln(1/κa)	.	(4.18)

That does not seem very interesting since it is only an approximate expression and we already have an estimate for λ . Here is the subtle part though: the approximations involved the “fuzzyness” of length scales κ−1 and a. The only thing we are going to assume concerning these two length scales is that κa 1. If you look at the self-consistency condition, you see that the functional dependence on κa imposes a condition on the exponent of κa, no matter what these two length scales precisely are. The exponent equals two on the left-hand side so it must equal two on the right-hand side as well! This means that (at least in the limit of low salt) λ = −e/lB exactly.

Actually, this is the solution only if the renormalized charge di ers from the bare charge per unit length, which is the case as long as |λ| > e/lB. There is another solution to the self-consistency equation, namely λ = λ ! Check yourself that this is the solution if |λ| < e/lB. There is thus a mathematical singularity in the dependence of the renormalized charge on the bare charge at the point |λ| = e/lB.

It is possible to compute the renormalized charge per unit length analytically from the non-linear BP equation [48] in the limit of zero salt and it confirms this result. From numerical solutions of the BP equation at finite salt concentration, we know that this mathematical singularity is “smeared-out” as the salt concentration increases.

You can apply this method – due to Oosawa [49] – also to a charged sphere of radius a, charge Z. Show yourself that in the large Z limit, the renormalized charge Z of a sphere is of order (a/lB) [50], the ratio of the radius and the Bjerrum length.

4.3.3 Primitive model: Free energy

If the analytical BP solution for an infinite rod is inserted in the free energy expression equation (4.4), you obtain in the strongcoupling limit of large

62	Physics of Bio-Molecules and Cells

Fig. 30. Dependence of the renormalized charge per unit length on the bare charge per unit length.

Manning Parameter ξ for the electrostatic free energy:

lim	kBT	2	2
		ln "2ξ /(κa) #		(4.19)
ξ→∞ f (ξ) = b

in the limit of low salt concentration (this result, due to Lifson and Katchalsky [51], dates from 1954!). Like the weak-coupling DH expression equation (4.7), the charging free energy is positive. That is surprising: you would expect that in the strong coupling limit the electrostatic free energy should be negative due to the free energy gain obtained when you bring positive and negative charges together after the charge is turned on. Such an enthalpic term is indeed present, but it is a factor of order 1/ξ smaller. The electrostatic free energy for large ξ in BP theory is dominated by the entropic contribution. Its origin lies in the entropy loss that is su ered by the ions drawn into the Manning cloud: when you “turn on” the charges from zero, counter-ions are forced to condense on the rod once ξ exceeds one. The condensed ions lose kBT per ion in the charging process, so the entropic contribution to the free energy per unit length is of order kBT per charge or kBT /b, which is indeed the order of magnitude of f . We sometimes call this e ect “counterion confinement”.

It is interesting to compare the entropic free energy of the counterions and the conformational free energy of a polymer. For DNA, the latter is of order kBT per persistence length. Since the persistence length is of order 500 ˚A, we see that the conformational free energy of DNA is completely negligible compared to the counter-ion free energy.

R.F. Bruinsma: Physics of Protein-DNA Interaction

63

4.4 Counter-ion release and non-specific protein-DNA interaction

4.4.1 Counter-ion release

Assume a positively charged macro-ion with a charge Z of order 10 or so approaching a highly negatively charged rod. For distances large compared to 1/κ, the electrostatic potential can be approximated by the asymptotic DH form. However, when the positive charge enters the Debye cloud unusual things start to happen. Recall that the counter-ions of the Manning cloud carry a free energy cost of about kBT per counter-ion. When the positive macro-ion charges are brought into close contact with the negative macroion charges, a certain number of condensed counter-ions can be released. If the number of released counterions equals Z < Z, then the free energy gain ∆FCR upon binding is:

∆FCR = Z	bf (ξ)
= Z	kBT ln "2ξ2/(κa)2# ·	(4.20)

This is a predominantly entropic binding mechanism. You might think of the highly charged rod with it condensed cloud of counter-ions as an entropic electro-chemical battery and the binding of the positive charge as a local discharge of this battery.

Let’s apply the idea of counter-ion release to protein-DNA interaction [52]. Most proteins associating with DNA have a small total charge, but a quite significant dipole moment. The protein surface that fits on the DNA is lined with positive charge and the surface facing away with negative charge. Z is then the number of positive charges on the DNAbinding surface of the protein. Note that this clever arrangement assists the “docking”, the proper orienting of the protein, as it approaches DNA, while it avoids generic association of the protein with other negatively charged biopolymers.

In Section 2, we discussed the fact that the non-specific interaction between the lac repressor and DNA is predominantly entropic. We now understand this at a fundamental level [53]: the entropy gain of the nonspecific interaction is due to release of the counter-ions, just like the entropic hydrophobic interaction can be viewed as being due to release of water molecules. Since the Debye Parameter is proportional to [Salt]1/2, ∆FCR should be proportional to − ln([Salt]) according to equation (4.19). This indeed agrees with the dependence on salt concentration of the non-specific interaction between the lac repressor and DNA given by equation (2.21). Comparing equations (2.21) and (4.19), we even can estimate the number Z of released counter-ions of the lac repressor to be about ten.

The predominantly entropic nature of the non-specific protein-DNA interaction informs us that the DH approximation is inappropriate for treating

64	Physics of Bio-Molecules and Cells

protein-DNA complexation because in the DH approximation, entropic and enthalpic contributions are comparable in magnitude, in disagreement with the experimental observations on the non-specific binding energy discussed in Section 2. In general, the use of DH potentials with renormalized charges is thus not appropriate for solutions containing macro-ions with opposite sign of charge, since that will lead to formation of complexes of macro-ions of opposite charge and counter-ion release of condensed counterions.

4.4.2 Nucleosome formation and the isoelectric instability

The most dramatic example of the non-specific protein-DNA interaction is the complexation of the positively charged nucleosome core with negatively charged DNA discussed in the previous section. The total positive charge of the core, Zcore, is about 245 elementary charges and the total negative charge of the wrapped DNA equals ZDNA = −292. That is curious: the net charge Z of the nucleosome is positive, about −47. It is not obvious why more DNA should be wrapped around the nucleosome than required to neutralize the core charge, assuming that electrostatics is the dominant association mechanism. If anything, it would be expected that Z is negative, because of the free energy penalty incurred when we bend the DNA around the nucleosome.

Let’s apply the concept of counter-ion release to nucleosome formation. We discussed, in Section 3, the Marky–Manning model for the formation of the nucleosome. In this model, the electrostatic attraction between DNA and the nucleosome core is characterized by an adhesion energy per unit length. If the binding of DNA to the nucleosome core is due to counter-ion release, then we can simply identify the adhesion energy per unit length with the f (ξ) given by equation (4.18). Within the counter-ion release model we would expect to release no more counter-ions than required to compensate the positive charge of the core. That again leads to the (intuitive) result that Z should be zero (or negative). Such neutralized, charge compensated complexes are known as “isoelectric” by the way.

Let’s return to the Oosawa description of counter-ion condensation and measure the electrostatic potential around an isoelectric nucleosome complex with Z = 0, using again a microscopic voltmeter. One of the electrodes of the voltmeter is placed in contact with the Manning cloud of the DNA far from the nucleosome and the other electrode is placed near the surface of the nucleosome (see figure). Let ∆Φ = V (DNA) − V (Nucleosome) be the read-out of the voltmeter. The Boltzmann distribution informs us that the ratio of (small) positive ion concentration at the two electrode locations

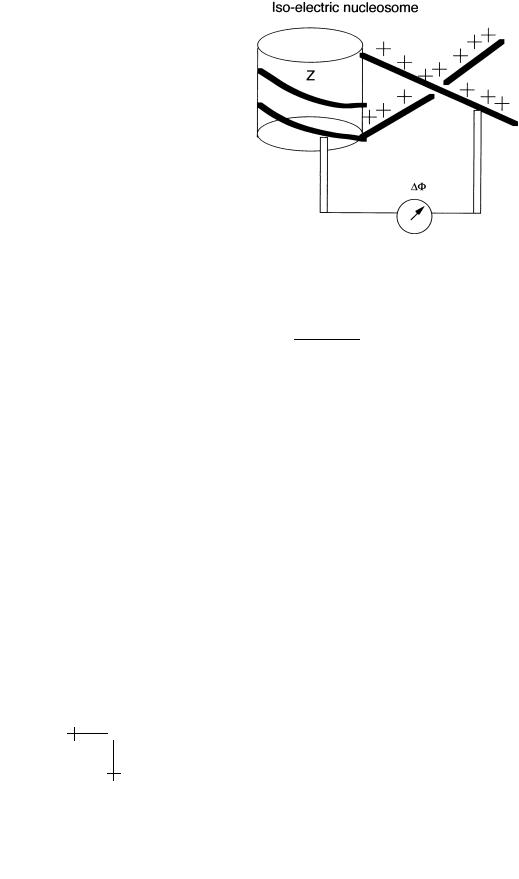
R.F. Bruinsma: Physics of Protein-DNA Interaction

65

Fig. 31. Measuring the electrical potential of a charge-neutral nucleosome.

under conditions of chemical equilibrium must equal:

CDNA	= exp(−e∆Φ/kBT ).	(4.21)
CNucleosome

Since the complex is charge neutral, the concentration of positive ions at the nucleosome surface must be low (not quite zero since the electrostatic potential surrounding the complex will contain higher order multipole contributions), while the ion concentration inside the Manning cloud is high as we saw (of order 1 M in fact). That means that the left-hand side of equation (4.20) must be large, so the voltage di erence ∆Φ must be large and negative to insure chemical equilibrium of the positive ions. The electrical potential at the nucleosome surface thus must exceed the potential at the DNA surface by a significant amount. This electrical potential di erence will “pull-in” extra DNA material leading to a deviation from charge neutrality, in fact to charge-reversal: by that we mean that the e ective charge Z of the complex has a di erent sign from the bare charge. Counter-ions are not released to infinity when this happens but instead remain associated with the charged nucleosome complex, but this still increases their entropy. As you wrap more and more DNA over the complex, the capacitive charging energy cost of the complex grows and eventually the wrapping process stops.

Let’s try to make this argument quantitative [54]. Assume a spherical nucleosome of radius a with bare charge Z and assume that a length L of DNA has been wrapped around it. The net charge Z (L) of the nucleosome

66	Physics of Bio-Molecules and Cells
equals:
	Z (L) = Z	−	(L/b)	(4.22)

with b the spacing between charges along DNA. At the isoelectric point

Z = 0, the wrapping length is Liso = Zb. The free energy is the sum of three terms. The bending energy cost, the adhesion energy per unit

length, and the capacitive charging contribution just mentioned. The first two terms were already present in the Marky–Manning model of Section 3, while the last term will be handled by treating the nucleosome as a sperical capacitor with capacitance 1/εa:

∆F = $	κ	− f (ξ)%L +	e2Z (L)2	(4.23)
	a2		εa

(we are not concerned here about numerical factors). The second term has a quadratic minimum at L = Liso, while the first linear term favors large L (at least in the relevant regime where the adhesion energy exceeds the bending energy). The optimal value L clearly must exceed Liso. After minimization with respect to L, we obtain:

a	ln(1/(κa)2) − κb/kBT a2 .	(4.24)
Z ≈ lB

The e ective net charge is predicted to be of the order of the ratio of the radius of the nucleosome and the Bjerrum length. Note that at the Marky–Manning unwrapping point, the e ective nucleosome charge vanishes. Interestingly, this e ective charge is of order the typical renormalized charge of a highly charged sphere in BP theory. We actually might have guessed our result right away!

This charge-reversal e ect is our final example of proper design. A classical biophysics experiment is the precipitation of proteins at the iso-electric point (by varying pH). A solution of isoelectric complexes aggregates under the action of the van der Waals attraction. If the nucleosomes would have been charge-neutral, they would have stuck together, even though DNA is highly charged. The e ective charge of the nucleosome prevents this unwanted aggregation. A subtle and counter-intuitive physical mechanism, counter-ion release, is recruited in the e cient management of the macroion household of the cell.

RB would like to thank the Les Houches center for its hospitality. I have enormously benefited in my work in this area from interaction with numerous colleagues, in particular William Gelbart, Itamar Borukhov, Andrea Liu, Jay Mashl, Stella Park, Fyl Pincus, Joseph Rudnick, Cyrus Safinya, and Helmut Schiessel.