Кулик Введение в теорию квантовых вычислений Книга 2 2008

получится состояние 0 , отвечающее нулевому значению двоичной переменной, а с вероятностью

w =		b		2	(2.9)
1

реализуется состояние 1 , отвечающее единице. Поэтому единст-

венным ограничением, накладываемым на амплитуды a и b, является условие нормировки

w + w =			a		2	+		b		2	=1	(2.10)
0	1

для полной вероятности.

Итак, в отличие от классической ячейки, которая может находиться либо в состоянии “0”, либо в состоянии “1”, произвольное состояние кубита оказывается таким, что в нем с некоторыми вероятностями, но одновременно, представлены и “0” и ”1”. Этот факт, однако, нельзя интерпретировать в терминах классической стохастической двоичной переменной, значения которой реализуются с той или иной вероятностью. Суть в том, что состояния вычислительного базиса входят в (2.7) в виде когерентной суперпозиции, комплексные коэффициенты которой определяют не только меру (вероятность) присутствия в квантовом состоянии кубита каждого из базисных векторов, но и фиксируют фазовое соотношение между ними. С учетом (2.10) комплексные амплитуды a и b можно представить в форме

	a = eiα cos	θ	,	b = eiβ sin	θ	,	(2.11)
		2			2

где α, β, θ – действительные параметры. Тогда (2.7) принимает вид

ψ	= eiα cos		θ			0		+eiβ sin		θ			1	=
			2							2								(2.12)
		iα		θ										θ
	= e							0 +e	i(β−α)		sin					1
		cos		2										2			.
								61

Если отвлечься от общего фазового множителя, который не меняет квантовое состояние и может быть опущен, то вектор ψ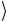 произ-

вольного состояния кубита определяется двумя действительными параметрами — углом θ и относительной фазой γ = β–α, о которой говорилось ранее.

Выражения (2.7) и (2.12) демонстрируют своеобразную природу информации, которая записана с помощью кубитов. Будем называть ее квантовой информацией. При этом кубит выступает как простейший элемент квантовой информации. Поскольку используемые для записи информации символы “0” и ”1” ставятся в со-

ответствие базисным состояниям 0 и 1 , то можно сказать с

определенной долей условности, что в произвольном состоянии кубита эти символы представлены в виде когерентной суперпозиции, которая содержит сведения о вероятностях и фазах. Как известно, фазовые соотношения играют определяющую роль в таком явлении как интерференция. Манипулирование квантовой информацией, например, в процессе вычисления будет определяться тем, как меняются квантовые состояния, т.е. сам процесс вычисления будет подчиняться квантовым законам. Другими словами, в таком процессе, который будем обозначать термином «квантовые вычисления», могут проявляться сугубо квантовые эффекты, такие, например, как одновременная эволюция вдоль разных путей, дифракция, интерференция. Тем самым открываются принципиально новые возможности для манипулирования информацией.

При выбранном базисе для любого вектора состояния кубита | ψ комплексные коэффициенты a и b в суперпозиции (2.7) или

(2.12) определяются однозначно. Действительно, из условий ортогональности (2.5) следует, что a и b имеют вид скалярных произведений

a = 0		ψ , b = 1		ψ ,	(2.13)

т.е. представляют собой “проекции” вектора | ψ на два базисных вектора. Взаимно однозначное соответствие между | ψ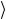 и

62

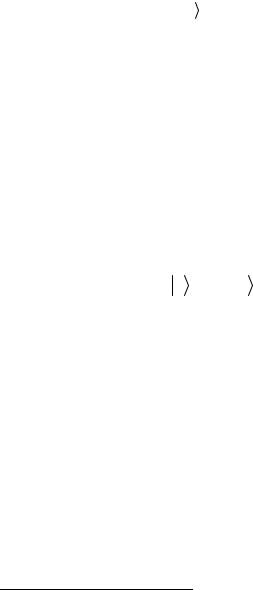
коэффициентами (2.13), т.е.

| ψ	a		,	(2.14)
	↔
	b

позволяет описывать состояние кубита с помощью вектор-столбца, составленного из пары комплексных чисел1 и изображенного в правой части соотношения (2.14). Напомним, что описание состояния с помощью вектор-столбца (2.14) называется матричным представлением (см. главу 1). С учетом параметризации (2.11) векторстолбец записывается в виде

a		=	exp(iα)cos(θ/ 2)		.	(2.15)
b			exp(iβ)sin(θ/ 2)

Базисным состояниям соответствуют вектор-столбцы вида

0		1		,		1		0		(2.16)
	=	0					=	1	.

Поэтому суперпозицию (2.7) можно представить в эквивалентной форме

a		= a		1		+b		0		.	(2.17)
				0				1
b

Это соотношение выражает стандартное правило матричной алгебры о покомпонентном умножении вектор-столбцов на комплексные числа и их сложении.

Свойства кубитов и законы, определяющие их поведение, неотъемлемы от тех физических систем, квантовые состояния которых используются в качестве кубита. Поэтому рассмотрим простые примеры физической реализации одного кубита.

1 Эту пару чисел можно рассматривать как функцию f(C)=<С|Ψ> двоич-

ной переменной С. Тогда a=<0|Ψ>=f(0), b= <1|Ψ>=f(1).

63

Примеры физических систем, реализующих кубиты

Важным и широко используемым для этой цели физическим объектом является фотон. Если не вдаваться в некоторые тонкости, связанные с квантовым описанием этой физической системы, то она представляется простой и наглядной; с фотонов началась квантовая механика и наш рассказ о ней в главе 1.

Состояние свободного фотона с волновым вектором k , т.е. с определенной частотой ω = kc и направлением пространственного движения, характеризуется еще и поляризацией. Поляризационное состояние задается1, единичным вектором e , который ортогонален

вектору k , т.е.

e 2 = 1, k e = 0.

(2.18)

Для определенности мы здесь говорим о линейной поляризации, когда вектор e действительный.

Отметим важное свойство рассматриваемого нами состояния свободного фотона. Оно состоит в том, что пространственные и поляризационные степени свободы являются фактически независимыми. Единственное ограничение заключается во взаимной ор-

тогональности векторов k и e (2.18). Поэтому кэт-вектор такого квантового состояния фотона удобно записать в факторизованном виде

			k , e =	k		e	,	(2.19)
		e отвечают, соответственно,
где	k и						пространственным и по-

ляризационной степеням свободы.

Далее мы будем говорить о поляризационном состоянии, кото-

1В классической электромагнитной волне этот вектор задает направление вектора напряженности электрического поля. В квантовой механике электромагнитному полю фотона отвечает векторный оператор. Тогда вектор

e описывает направление векторного оператора электрического поля.

64

рое описывается кэт-вектором e .

В плоскости, ортогональной вектору k , можно выбрать два

линейно независимых		базисных			вектора	поляризации			e 1 и e 2,
удовлетворяющих условиям
e 2	= e2	= 1, e	e	2	= k e	= k e	2	= 0 .	(2.20)
1	2	1			1

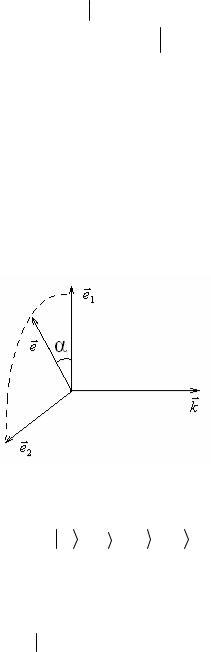
Эта тройка векторов изображена на рис. 2.1

На этом же рисунке показан произвольный вектор поляризации e , который, очевидно, можно разложить по базисным векторам

e = e1 cosα + e2 sinα .

(2.21)

Рис. 2.1

Два линейно независимых поляризационных состояния

e1 ≡ | 0 ,

e2 ≡ |1

(2.22)

можно выбрать в качестве базисных состояний кубита. Они удовлетворяют необходимым условиям ортонормированности и полноты (2.4)-(2.6). Линейную комбинацию базисных состояний (2.22), аналогичную разложению (2.21), можно отождествить с поляриза-

ционным состоянием e . Произвольное состояние поляризацион-

65

ного кубита описывается выражением (2.7) с произвольными комплексными амплитудами a и b. В дальнейшем мы будем использовать и другие обозначения для базисных состояний поляризационного кубита, например, с помощью букв v и h

e1 ≡		v ≡		0 ,		e2 ≡		h ≡		1 ,	(2.23)

которые показывают вертикальную (v) и горизонтальную (h) линейные поляризации. В оптике широко используется циркулярнополяризованные фотоны. Состояния фотона с правой и левой поляризациями, которым отвечают комплексные векторы

e± ≡ e1 ± i e2 ,

(2.24)

тоже могут быть использованы в качестве базисных состояний поляризационного кубита.

Целый ряд впечатляющих экспериментов, таких как проверка неравенств Белла, квантовая телепортация, которые продемонстрировали возможности манипулирования квантовой информацией, был выполнен с кубитами, построенными на поляризационных состояниях фотонов.

Еще одним примером физической системы, которая, можно сказать, самой природой создана для реализации кубита, является частица со спином s = 1/2, т.е. имеющая собственный механический момент s. Наличие такого момента является сугубо квантовым свойством, не имеющим аналога в классической физике. Общие свойства оператора спина 1/2 и спиновых состояний рассматриваются в разделе 2.2. Сейчас мы используем только некоторые из них.

Проекция спина 1/2 на любую ось может принимать только два значения: +1/2 и –1/2. Два спиновых состояния

Sz	=	1	≡		0	и	Sz	= −	1	≡		1	(2.25)
		2							2

с определенными значениями проекции спина на некоторую ось z, которую называют осью квантования, образуют полный набор спиновых состояний. Они выбираются в качестве базисных состояний кубита и, с определенной долей условности, изображены на рис.2.2.

66

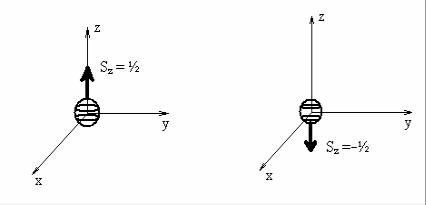
Рис. 2.2

Ось квантования может быть выбрана произвольно. Если же в системе есть какое-либо выделенное направление, заданное, например, внешним магнитным полем, с помощью которого манипулируют кубитами, то это направление обычно и выбирается в качестве оси квантования z.

Многие частицы — электроны, нейтроны, протоны и другие обладают спином 1/2 и в принципе могут быть использованы для реализации кубитов на спиновых состояниях. При этом надо помнить о пространственных степенях свободы. С ними могут быть связаны определенные трудности, так как эффективное манипулирование спиновыми кубитами предполагает в принципе, что они достаточно хорошо локализованы в пространстве.

Внастоящее время для экспериментальной реализации спино-

вых кубитов используется атомные ядра со спином 1/2 такие, например, как 1Н, т.е. ядро водорода – протон, изотоп углерода 13С, ядро азота 15N, которые входят в состав больших органических молекул. Пространственное расположение этих кубитов определяется внутримолекулярным взаимодействием. Воздействие на кубиты осуществляется с помощью магнитных полей разной конфигурации и основано на эффекте Зеемана для ядерных магнитных моментов. Такие подходы детально разработаны в методе ядерного магнитного резонанса (ЯМР).

Вкачестве кубита, наконец, можно использовать два внутрен-

67

них (электронных) состояния атома или иона. Перспективность таких систем обусловлена структурным многообразием связанных атомных состояний. В качестве базисных состояний используются, например, две компоненты тонкой или сверхтонкой структуры атомного спектра, которые разделены малым энергетическим интервалом. Такую двухуровневую систему иногда называют энергетическим спином. Ее управление осуществляется с помощью резонансного микроволнового поля. Существенным фактором является то, что с помощью внешних электромагнитных полей, действующих на других переходах той же атомной системы, можно осуществить эффективное охлаждение и пространственную локализацию атомов и ионов.

2.2.Однокубитовые гейты

Сфизической точки зрения, кубит эквивалентен спиновой подсистеме частицы со спином S=1/2. Поэтому при описании состояний кубита и способов манипулирования этими состояниями мы будем использовать свойства спиновых состояний и операторов, действующих на спиновую переменную. Напомним сначала некоторые общие положения квантовой механики, касающиеся понятия спина.

Наличие спиновой степени свободы является сугубо квантовым свойством частиц, которого нет в классической физике. Спин выступает как квантовое число, определяющее трансформационные свойства состояния квантового объекта по отношению к преобразованию поворота системы координат.

Так, при повороте системы координат на угол Ф вокруг оси, на-

правление которой задано единичным вектором n , состояние частицы, обладающей тем или иным спином, преобразуется по закону:

ψ'	ˆ	(2.26)
	= exp(iФn S ) ψ .

Это есть унитарное преобразование1, генератором которого является эрмитовый векторный оператор спина

1 Понятие унитарного оператора обсуждается в этом разделе ниже.

68

Gˆ	ˆ	ˆ	ˆ			(2.27)
S	={ S x ,	S y ,	S z }.
			ˆ	ˆ	ˆ	проекций
Его компоненты, т.е. эрмитовые операторы Sx ,				S y ,	Sz

спина на координатные оси x, y, z, подчиняются следующим коммутационным соотношениям:

ˆ ˆ	ˆ ˆ	ˆ ˆ		ˆ	,	(2.28)
[ S j Sk ] =	S j Sk	– Sk S j	= i εjkl Sl
где индексы j, k, l пробегают значения x, y, z,				а	εjkl	– антисиммет-

ричный тензор третьего ранга. Из этих коммутационных соотношений следует, что эрмитовый неотрицательный оператор

Gˆ	2	ˆ 2	ˆ 2	ˆ	2	(2.29)
S		= Sx	+ S y	+ Sz

коммутирует со всеми генераторами ˆ , ˆ , ˆ , но сами эти опе-

S x S y S z

раторы, как видно из (2.28), между собой не коммутируют. Поэтому в качестве полного набора наблюдаемых можно взять два эрми-

Gˆ	2	ˆ
товых оператора S		и S z , которые коммутируют между собой и

обладают полной общей системой собственных состояний. При

Gˆ	2	равны
этом собственные значения оператора S

S(S+1),

где неотрицательное число S называется спином частицы и может быть либо целым, либо полуцелым. Подчеркнем, что величина спина есть фундаментальное свойство квантовой частицы.

При данном S полный набор спиновых состояний характеризу-

ется собственными значениями оператора ˆ проекции спина на

S z

ось z, которые представляют собой целые или полуцелые числа, лежащие в пределах от ─S до S через единицу. Таким образом,

69

полный набор включает

2S +1

базисное спиновое состояние с определенными значениями проекции спина на ось квантования z. Такое описание называется Sz – представлением.

В качестве оси квантования можно выбрать и любую другую ось. При данном S проекция спина на эту ось также будет принимать целые или полуцелые значения от –S до S через единицу, т.е. всего 2S+1 значение. Использование такого базиса означает просто переход к другому унитарно эквивалентному представлению и никак не влияет на физическую картину. Действительно, чтобы осуществить такой переход, надо повернуть исходную систему координат и совместить ее ось z с направлением новой оси квантования. Тогда старый и новый базисы связаны унитарным преобразованием (2.26)

Перейдем теперь к более детальному обсуждению интересующего нас конкретного случая спина 1/2.

Спиноры и матрицы Паули

Если S=1/2, то 2S+1=2, и два базисных состояния имеют вид (2.25). Произвольное спиновое состояние описывается кэтвектором (2.12) или эквивалентным ему двухкомпонентным столб-

цом (2.15), т.е.

a exp(iα)cos(θ/ 2)

ψ = = . (2.30)

b exp(iβ)sin(θ/ 2)

Такой вектор-столбец называется спинором первого ранга или просто спинором. При этом параметры α, β и θ имеют наглядный физический смысл, а именно, они задают, как это показано на

рис. 2.3, пространственную ориентацию вектора < S >, который представляет собой среднее значение операторного вектора спина

70