
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf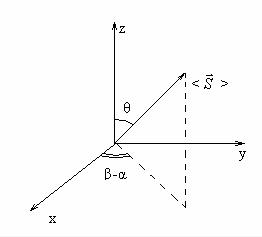
ˆ в состоянии (2.30). Длина этого вектора |< >|= 1/2 .
S S
Рис. 2.3
Доказательство этих утверждений, т.е. вычисление компонент век-
тора < S >, приведено в задаче 2 в конце данного раздела.
Так как спинор (2.30) написан в Sz-представлении, то его верхняя (нижняя) компонента имеет смысл амплитуды вероятности обнаружить первое (второе) базисное состояние, указанное в (2.25), при измерении проекции спина на ось z. Сами вероятности получить то или иное значение проекции определяются, соответствен-
но, выражениями: |
|
|
|
w(Sz = 1/2) = cos2 θ |
, |
w(Sz = –1/2) = sin2 θ . |
(2.31) |
2 |
|
2 |
|
Таким образом, в произвольном спиновом состоянии, которое описывается кэт-вектором (2.12), проекция спина на ось квантования z не имеет определенного значения. Но всегда можно выбрать такую ось n , что проекция спина на эту ось будет иметь определенное значение (см. задачу 3 в конце данного раздела). Для полноты картины отметим, что базисным состояниям (2.25) соответствует спиноры (2.16), т.е.
71

|
Sz = |
1 |
≡ |
|
0 |
= |
|
1 |
|
, |
|
Sz |
|
= − |
1 |
|
0 |
|
, (2.32) |
|
|
|
|
|
|||||||||||||||||
|
|
|
0 |
|
|
|
≡|1 >= |
1 |
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а произвольный |
|
спинор |
|
записывается |
в |
виде суперпозиции |
||||||||||||||
(см. (2.7), (2.12), (2.17)): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
| ψ |
= |
a |
|
|
1 |
|
|
0 |
|
|
|
(2.33) |
|||||
|
|
|
|
|
= a |
|
+b |
. |
|
|
||||||||||
|
|
|
|
|
|
|
b |
|
|
0 |
|
|
1 |
|
|
|
|
|||
Перейдем теперь к рассмотрению линейных операторов, действующих в двумерном пространстве спиновых состояний.
ˆ |
по- |
Пусть в результате действия оператора F на состояние | ψ |
лучается состояние Φ , т.е.
, т.е.
ˆ |
= Φ . |
(2.34) |
F | ψ |
Записываем кэт-векторы | ψ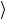 и Φ
и Φ в виде разложений
в виде разложений
| ψ = ∑ac | c > , |
|
Φ = ∑bc' | c'> |
(2.35) |
|
|||
c=0,1 |
|
c'=0,1 |
|
по базисным состоянием (2.32) и подставляем в уравнение (2.34).
Используя свойство линейности оператора ˆ
F , имеем
Φ |
ˆ |
|
ˆ |
= ∑bc' | c'> = F |
∑ac | c > = ∑ac F | c > , |
||
|
c'=0,1 |
c=0,1 |
c=0,1 |
72

т.е.
∑bc' | c' > = |
ˆ |
(2.36) |
∑ac F | c > . |
||
c'=0,1 |
c=0,1 |
|
Проектируя обе части этого уравнения на базисные векторы c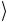 с учетом условий их ортонормированности, получаем
с учетом условий их ортонормированности, получаем
ˆ |
∑Fc'c ac , (c`=0, 1) . |
(2.37) |
bc’ = ∑< c'| F | c > ac ≡ |
||
c=0,1 |
c=0,1 |
|
Совокупность четырех комплексных чисел |
|
|
Fc'c = < c'| |
ˆ |
(2.38) |
F | c > , (c, c’=0, 1) |
||
образует 2x2 матрицу оператора ˆ в базисе (2.32). Выражение
F
(2.37) показывает, что спинор, описывающий состояние
Φˆ
=F | ψ ,
получается из спинора, соответствующего состоянию | ψ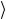 ,
,
как результат умножения слева (по стандартным правилам матричной алгебры) на матрицу Fc'c , которая представляет линейный
оператор ˆ , т.е.
F
b |
|
F F |
a |
|
F a |
+ F a |
|
(2.39) |
|
0 |
|
= 00 |
01 |
0 |
|
= 00 0 |
01 1 |
. |
|
b1 |
F10 |
F11 a1 |
F10 a0 + F11a1 |
|
|||||
Итак, спиновые состояния образуют двумерное гильбертово пространство и описываются спинорами. Действующие в этом пространстве линейные операторы имеют вид матриц 2x2, что вполне естественно, поскольку оператор преобразует линейным образом две компоненты одного спинора в две компоненты другого спино-
73
ра, а две линейные комбинации из двух величин содержат четыре коэффициента.
Среди всего многообразия линейных операторов фундаментальную роль играет сам векторный оператор спина. Поэтому рассмотрим матрицы компонент оператор спина
ˆ |
ˆ |
ˆ |
ˆ |
S |
= { Sx , |
S y , |
Sz }, |
которые в дальнейшем будут широко использоваться при описании различных логических операций с кубитами.
В Sz-представлении для спина 1/2 эти матрицы записываются в следующем виде:
|
|
|
|
ˆ |
|
1 |
|
|
ˆ |
|
1 |
|
|
|
ˆ |
|
1 |
|
|
||
|
|
|
|
Sx |
= |
|
σ x , S y |
= |
|
|
σ y , |
Sz |
= |
|
|
σ z , |
(2.40) |
||||
|
|
|
|
2 |
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
0 |
1 |
, σ |
|
= |
0 |
−i |
, σ |
|
= |
1 |
0 |
(2.41) |
||||||
x |
= |
|
|
y |
|
|
|
|
z |
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
0 |
|
|
|
0 |
|
||||||||
|
|
|
0 |
|
|
|
|
i |
|
|
|
|
|
−1 |
|
||||||
и называются матрицами Паули. Поскольку в качестве базиса ис-
пользуются собственные состояния (2.32) оператора ˆ
Sz , то матри-
ца этого оператора согласно (2.38) является диагональной, а на диагонали стоят собственные значения +1/2 и –1/2. Так как опера-
ˆ |
ˆ |
ˆ |
(см.(2.28)), то они представля- |
торы Sx , |
S y |
не коммутируют с Sz |
ются недиагональными матрицами. Приведенный в (2.40) и (2.41) явный вид этих матриц следует из коммутационных соотношений (2.28). Более подробно этот вопрос рассматривается в задаче 1 в конце этого раздела.
Сформулируем основные свойства матриц Паули, которые нам понадобятся в дальнейшем.
1. Матрицы Паули являются эрмитовыми матрицами
σi+ = σi , i = x, y, z. |
(2.42) |
74 |
|
2.Единичная матрица и три матрицы Паули образуют полный набор матриц 2x2, т.е. любую матрицу М можно представить в следующем виде:
M= a0 + a1 σ x + a2 σ y + a3 σz ≡ a0 + aσ . |
(2.43) |
3.Произведение матриц Паули обладает следующим свойством:
σ j σk = δjk + iεjkl σ1 (j, k, l = x, y, z) . |
(2.44) |
Это соотношение означает, в частности, что
σ x2 =σ y2 =σ z2 =1. |
(2.45) |
Если взять произведение разноименных матриц Паули, то, например,
σ x σ y = –σ y σ x = iσz . |
(2.46) |
Это и еще два соотношения, которые получаются из (2.46) циклической перестановкой индексов x, y, z, означают, что разноименные матрицы Паули антикоммутируют друг с другом. Свойства (2.42), (2.45) и (2.46) легко проверить непосредственными вычислениями, используя явный вид (2.41) матриц Паули. При этом соотношение (2.44) представляет собой единую форму записи свойств (2.45) и (2.46). Соотношение (2.43) более подробно обсуждается в задаче 4 в конце раздела.
Иногда вместо матриц Паули (2.41) удобно использовать соответствующие им операторы, записанные с помощью внешних произведений (см. главу 1) базисных векторов (2.32). В соответствии с определением (2.38) матричных элементов
75

(см. задачу 6 в конце раздела) эти операторы имеют вид
σ x |
≡ σ1 |
= |Sz = |
1 |
|
Sz = – |
1 |
|
| + |Sz |
= – |
1 |
Sz = |
|
1 |
| = |
||||||||||||
2 |
|
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
= |0 1|+|1 0| , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
iσ y |
≡ iσ 2 |
= |Sz = |
|
1 |
Sz = – |
1 |
| – |Sz = – |
1 |
Sz = |
|
1 |
| = |
||||||||||||||
|
2 |
2 |
2 |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
=|0 1|−|1 0| |
, |
|
|
|
|
|
|
|
|
|
|
(2.47) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
σ z |
≡ σ3 |
= |Sz = |
|
1 |
Sz = |
1 |
| – |Sz = – |
1 |
|
Sz = – |
1 |
|
| = |
|||||||||||||
2 |
|
2 |
|
2 |
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
=|0 0|−|1 1| .
Здесь для полноты картины представлены все используемые нами обозначения базисных векторов — как с помощью квантового чис-
ла Sz = ± 12 , так и с помощью значений С = 0, 1 двоичного числа.
Заметим также, что индексы x, y, z могут быть заменены соответственно на 1, 2 и 3.
Унитарные преобразования и однокубитовые гейты
Остановимся более подробно на свойствах линейного оператора
ˆ |
ˆ |
|
iΦ nS |
(2.48) |
|
R(Φ, n) = e |
, |
который определяет закон преобразования (2.26) спинового состояния при повороте системы координат на угол Φ вокруг оси, заданной единичным вектором n . Повороту на угол ─Φ вокруг
76
той же оси отвечает, очевидно, оператор
ˆ |
|
ˆ |
e |
−iΦ nS |
|
R(−Φ, n) = |
|
для которого выполняются условия
ˆ |
−1 |
(Φ, n) , |
(2.49) |
≡ R |
|
ˆ ˆ −1 |
ˆ −1 |
ˆ |
(2.50) |
RR |
= R |
R = 1 , |
т.е. он является обратным по отношению к оператору ˆ . Входя-
R
щий в показатель экспоненты в формулах (2.48) и (2.49) оператор
ˆ |
ˆ |
ˆ |
|
ˆ |
ˆ |
(2.51) |
Sn |
≡ nS |
= nxSx |
+ ny S y |
+ nz Sz |
||
проекции спина на ось n является эрмитовым, |
|
|||||
|
|
ˆ |
+ |
ˆ |
|
|
|
|
Sn |
|
= Sn . |
|
|
Тогда при эрмитовом сопряжении оператора ˆ получаем, учиты-
R
вая (2.49), что
|
|
|
ˆ |
|
|
|
|
ˆ |
+ |
(Φ, n) = e |
−iΦ nS |
ˆ |
−1 |
(Φ, n) , |
(2.52) |
R |
|
|
≡ R |
|
т.е. эрмитово сопряженный оператор совпадает с обратным. Этим свойством определяется важный класс так называемых унитарных
операторов. А именно, оператор ˆ , у которого существует обрат-
U
ˆ |
−1 |
|
ˆ |
+ |
, т.е. |
ный оператор U |
|
, совпадающий с U |
|
||
|
|
ˆ −1 |
ˆ + |
, |
(2.53) |
|
|
U |
=U |
||
называется унитарным. Условие (2.53) можно представить в экви-
валентной форме, умножая его слева или справа на оператор ˆ .
U
77

В результате получаем
ˆ ˆ + |
ˆ |
+ ˆ |
(2.54) |
U U |
=U |
U =1. |
Из этого соотношения следует, что скалярное произведение векторов состояний инвариантно относительно унитарного преобразова-
ния. Действительно, пусть действие унитарного оператора ˆ
U име-
ет вид
|
|
|
|
' |
ˆ |
|
ψ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ψ1 |
=U |
|
|
|
|
|
|
|
|
' |
ˆ |
|
ψ2 |
|
' |
|
= |
ψ2 |
|
ˆ + |
. |
||
|
|
|
|
||||||||||
ψ2 |
=U |
|
, т.е. ψ2 |
|
|
U |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда
' |
|
' |
= ψ2 |
|
ˆ |
+ ˆ |
|
ψ1 = ψ2 |
|
ψ1 . |
(2.55) |
|
|
|
|
||||||||
ψ2 |
|
ψ1 |
|
U |
U |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Это важное свойство означает, что при унитарном преобразовании сохраняются условия нормировки и ортогональности векторов состояний. Кроме того, существование обратного оператора гарантирует взаимно однозначное соответствие между состояниями, которые получаются друг из друга под действием унитарного оператора. Из сказанного выше следует, что унитарный оператор преобразует один полный набор базисных состояний системы в другой полный набор. При этом все гильбертово пространство состояний квантовой системы переходит само в себя с сохранением своей линейной структуры, а также метрики, основанной на скалярном произведении.
Благодаря указанным свойствам, именно унитарные преобразования играют ключевую роль в процессах манипулирования квантовой информацией. Суть в том, что, сохраняя во всей полноте память о фазовых соотношениях между компонентами любой суперпозиции квантовых состояний, унитарные преобразования сохраняют весь “объем” записанной с помощью этой суперпозиции квантовой информации. При этом информация не стирается, и весь
78
процесс манипулирования ею является обратимым. Проблема обратимости вычислений, в частности, ее термодинамический аспект, обсуждается в разделе 2.6.
Унитарные операции, производимые над кубитами, называются квантовыми логическими гейтами. Начнем с простейшего случая однокубитовых гейтов, которым отвечают унитарные преобразования в двумерном гильбертовом пространстве спиновых состояний для S = 1/2.
Из свойств (2.42) и (2.45) следует, что сами матрицы Паули являются унитарными, σi+ = σi =σi−1 , поэтому они описывают некоторые элементарные логические операции. Рассмотрим, например, действие матрицы (или операторы) σ1 на базисные векторы. Используя (2.41) и (2.47), получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
1 0 1 |
1 |
0 |
|
(2.56) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
= |
1 0 |
|
= |
|
|||||||||||||||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
0 1 |
|
|
|
+ |
|
|
|
|
1 |
0 |
|
|
|
) |
|
|
|
0 |
= |
|
|
0 |
1 |
|
0 + |
|
1 |
0 |
|
0 = |
|
1 , |
(2.57) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
так как |
1 |
|
0 |
|
|
|
= 0 , а |
0 |
|
0 |
|
|
|
=1. Аналогично, имеем |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1 |
|
|
|
|
0 0 1 |
0 |
1 |
(2.58) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 0 |
1 |
0 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
0 1 |
|
+ |
|
|
1 |
0 |
|
|
) |
|
1 = |
|
0 1 |
|
1 + |
|
1 0 |
|
1 = |
|
0 , |
(2.59) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
так как |
0 |
|
1 = 0 , |
а |
1 |
|
1 =1. |
|
|
σ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Таким образом, |
|
|
|
|
операция |
|
|
|
|
переворачивает кубит, т.е. |
|||||||||||||||||||||||||||||||||||||||||||||||
0 ↔ 1
↔ 1 , что соответствует логическому гейту NOT (НЕ). Графическое изображение гейта NOT представлено на рис. 2.4. Слева
, что соответствует логическому гейту NOT (НЕ). Графическое изображение гейта NOT представлено на рис. 2.4. Слева
79
показано, как начальное |
состояние кубита |
C |
переходит в ко- |
||
нечное состояние |
|
C' . |
Крестиком обозначена |
операция NOT. |
|
|
|||||
Справа приведена таблица истинности для начального С и конечного С’ значений двоичной переменной, идентифицирующей состояние кубита.
|
C |
|
C' |
NOT: |
|
||
|
|
|
|||||
|
|
|
С |
С’ |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
||
Рис. 2.4
Операция σ3 приводит к обращению относительной фазы. Действительно, если подействовать σ3 на произвольное состояние кубита, то, используя (2.41) и (2.47), получим
a 1 |
0 a |
a |
(2.60) |
|||
σ3 |
= |
0 |
|
= |
|
|
b |
|
−1 b |
|
−b |
|
|
или
( 0 0 − 1 1 )((a 0 +b 1 )= a 0 0 0 + a 1 1 0 +
(2.61)
+b 0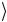
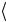 0 1
0 1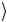 +b 1
+b 1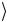
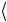 1 1
1 1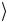 = a 0
= a 0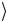 −b 1
−b 1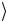 .
.
Более сложный однокубитовый гейт, который описывается оператором,
P(φ) ≡ |
|
0 0 |
|
+eiφ |
|
1 1 |
|
, |
(2.62) |
|
|
|
|
приводит к сдвигу относительной фазы на величину φ. В частности, если φ= π, то P(π) =σ3 , и мы получаем предыдущий случай.
80
