
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
требованиям, которые предъявляются к описанию квантового состояния.
|
6. Если подсистема А совпадает со всей |
системой, либо |
|||||||||||||||||||||||
сnν=AnBν, так |
что |
|
|
кэт-вектор |
|
|
ψAB |
|
факторизуется, |
||||||||||||||||
|
|||||||||||||||||||||||||
|
ψAB = |
|
ϕA |
|
χB , |
|
то подсистема А находится в чистом состоя- |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
нии с кэт-вектором |
|
ϕA |
и ее оператор плотности имеет вид |
||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
ρˆ A = SpB |
|
( |
|
ϕA |
|
|
χB χB |
|
ϕA |
|
) |
|
|
(1.103) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
SpB |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
= |
ϕA ϕA |
χB χB |
= |
ϕA ϕA |
. |
|||||||||||||||
Это выражение показывает, что любому чистому состоянию ψ
тоже можно сопоставить оператор плотности |
|
ρˆ = ψ ψ , |
(1.104) |
который представляет собой эрмитовый оператор проектирования. Из (1.103) или (1.104) следует, что матрица плотности чистого состояния удовлетворяет условию
ρˆ 2 = ρˆ, Spρˆ 2 = Spρˆ =1. |
(1.105) |
Для произвольного состояния с матрицей плотности (1.97) имеем
SpA(ρˆ 2A) = SpA ∑ pi p j ( |
|
i i |
|
)( |
|
j j |
|
)= |
||||||
|
|
|
|
|||||||||||
|
ij |
|
|
|
|
|
|
|
|
(1.106) |
||||
= ∑ pi2SpA ( |
|
i i |
|
)= ∑ pi2 |
||||||||||
|
|
≤1. |
||||||||||||
|
|
|||||||||||||
i |
|
|
|
|
|
|
|
|
i |
|
|
|
||
Поскольку ∑ pi =1, то равенство имеет место только тогда, когда i
все собственные значения рi, кроме одного, равны нулю, т. е. ρˆ A
является оператором плотности чистого состояния. Таким образом, условие (1.105) является критерием чистого состояния. Если же оно не выполнено, то состояние является смешанным.
Разложение (1.97) можно интерпретировать следующим образом. В состоянии, которое описывается матрицей плотности, заданы только вероятности pi присутствия тех или иных чистых со-
стояний i . О совокупности величин {pi , i
. О совокупности величин {pi , i }говорят как об ансамбле, реализующем состояние, которое описывается матрицей
}говорят как об ансамбле, реализующем состояние, которое описывается матрицей
51
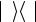
плотности ρˆ A (1.97) (И. фон Нейман). Никакой фазовой информа-
ции выражение (1.97) не содержит. В этом смысле состояние, которое описывается матрицей плотности, является некогерентной смесью чистых состояний. Этим оно принципиально отличается от суперпозиции чистых состояний, которая содержит фазовые соотношения между составляющими ее компонентами.
Отсутствие в выражении (1.97) фазовой информации означает, что описание с помощью матрицы плотности является менее полным, чем с помощью кэт –вектора. Эта неполнота описания является органическим свойством рассмотренных нами состояний подсистем, входящих в составную квантовую систему. Ее нельзя понимать как незнание каких-то характеристик квантового объекта. Просто есть такие квантовые состояния, которые допускают описание не с помощью кэт-вектора, но только с помощью матрицы плотности. Забавно отметить, что матрица плотности возникает, если угодно, когда мы применяем принцип суперпозиции для состояний (1.91) составной системы. В этой ситуации матрица плотности служит способом описания отдельных подсистем, входящих
всоставную квантовую систему. Тот факт, что состояния подсистем А и В оказываются скоррелированными, играет, как мы увидим
вглаве 2, ключевую роль в теории квантовой информации.
Взаключение коснемся информационного аспекта понятия квантового состояния. Мерой информации, которая содержится в квантовом состоянии физической системы, служит энтропия фон Неймана. Чем больше энтропия рассматриваемого объекта, тем меньше его информационное содержание. В этом суть естественного соответствия между количеством информации и энтропией.
Энтропия квантового состояния с матрицей плотности ρˆ |
опреде- |
ляется формулой |
|
S(ρˆ) = −Sp (ρˆ log2 ρˆ ). |
(1.107) |
Воспользуемся спектральным разложением (1.97) оператора плотности. По определению спектрального разложения функции от оператора имеем
log2 ρˆ = ∑(log2 p j ) j j . |
(1.108) |
j
52

Подставляя (1.97) и (1.108) в формулу (1.107), получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sp (ρˆ log2 ρˆ )= Sp∑(pi |
|
i |
i |
|
) |
∑log2 p j |
|
j j |
|
|
= |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|||||||||
= Sp∑ pi log2 p j |
|
i i |
|
|
j |
j |
|
= ∑ pi log2 piSp |
|
i |
|
i |
|
= (1.109) |
|||||||
|
|
|
|
|
|
||||||||||||||||
ij |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
= ∑ pi log2 pi. i
Здесь мы воспользовались условием ортонормированности
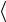 i j
i j = δij базисных состояний и правилом вычисления следа
= δij базисных состояний и правилом вычисления следа
Sp i
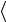 i =
i =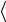 i i
i i =1.
=1.
Таким образом энтропия фон Неймана имеет вид
S(ρˆ) = −∑ p |
log |
p |
(1.110) |
i |
|
2 i |
|
i
и по форме совпадает с классической энтропией Шеннона. Вероятность изменяется в интервале 0 ≤ pi ≤ 1, поэтому энтропия S ≥ 0, а
ееминимальное значение равно нулю.
Легко видеть, что минимальное значение S = 0 реализуется то-
гда и только тогда, когда состояние системы является чистым, т. е. описывается кэт-вектором ψ . Действительно, в этом случае мат-
. Действительно, в этом случае мат-
рица плотности имеет вид (1.104), т. е. ее спектральное разложение содержит только одно слагаемое с коэффициентом р = 1. Поэтому
S = –1 log21 = 0.
Таким образом, энтропия чистого состояния имеет минимальное возможное значение, и мы говорим, что в состоянии, которое опи-
сывается кэт-вектором ψ , содержится наиболее полная возмож-
, содержится наиболее полная возмож-
ная в квантовой механике информация о данной физической системе.
Для иллюстрации вычислим энтропию фон Неймана для смешанного состояния. Пусть спектральное разложение (1.97) оператора плотности содержит только два слагаемых с р1= р2=1/2. Тогда
S(ρˆ) = −( p1 log2 p1 + p2 log p2 ) = log2 2 =1. |
(1.111) |
53 |
|
Это значение энтропии является максимально возможным для системы, которая может находиться только в двух состояниях. Поэтому информационное содержание квантового состояния, которое описывается рассмотренной матрицей плотности, является минимальным.
Список используемой литературы (источники)
1.Дирак П.А.М. Принципы квантовой механики. — М.: Физматгиз, 1960.
2.Мессиа А. Квантовая механика. Т. 1. — М.: Наука, 1979.
3.Боум А. Квантовая механика. Основы и приложения. — М.: Мир, 1990.
4.Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. — М.: Наука, 2006.
5.Давыдов А.С. Квантовая механика. — М.: Физматгиз, 1963.
54
«Квантовая механика – это полная загадок и парадоксов дисциплина, которую мы не понимаем до конца, но умеем применять.»
Марри Гелл-Ман
Инструментарий квантовых вычислений
Г л а в а 2
ИНСТРУМЕНТАРИЙ КВАНТОВЫХ ВЫЧИСЛЕНИЙ
______________________________________________________
Содержание
Кубиты. Однокубитовые гейты. Многокубитовый регистр. Перепутанные состояния. Двухкубитовые гейты. Мультикубитовые гейты.
Для записи единицы информации одного бита используется ячейка, представляющая собой некоторый физический элемент, который имеет два устойчивых состояния. Такой элемент называют триггером. В качестве такого элемента обычно используется полупроводник. Для наглядности можно говорить, например, о некоторой области с достаточно высокой концентрацией примесей, которыми допирован полупроводник. Тогда физически различимые состояния определяются, например, отсутствием или наличием заряда (потенциала) на такой примеси. Это могут быть токи в микроконтурах электронной схемы, сверхпроводящие элементы с джозефсоновскими контактами, квантовые точки и т.д., и т.п. Состояния триггера отождествляются с нулем (0) и единицей (1) и, тем самым, реализуют два значения бита информации.
Следует подчеркнуть, что практически используемые в настоящее время те или иные ячейки для записи единицы информации являются вполне макроскопическими физическими системами, содержащими большое число таких собственно квантовых объектов как атомы или электроны. Когда мы говорим, что ячейка заряжена (или не заряжена), то речь идет о вполне макроскопическом заряде, который на несколько порядков больше заряда электрона
e = 4,80 10-10 ед. СГСЭ. Другими словами, атрибуты информации
(логические 0 и 1) связаны с макроскопическими характеристиками триггера. Конечно, поведение зарядов, токов, потенциалов определяется физическими, как правило, квантовыми законами. Именно эти законы определяют такие важные характеристика как скорости необратимых релаксационных процессов, степень чувствительности системы к воздействию управляющих элементов и возможные механизмы таких воздействий.
56
Вся архитектура систем обработки информации, их масштабируемость, объем памяти, быстродействие имеют отчетливую тенденцию к миниатюризации составных элементов, реализуемость которой неразрывно связана с физическими законами. О степени миниатюризации можно судить по минимальному контролируемому размеру в архитектуре микросхем. Эту величину называют топологическим стандартом. На сегодняшний день он составляет 45 нм. Моноатомный слой в виде площадки с таким линейным размером содержит порядка 1.5 – 2 тыс. атомов. Тогда в ячейку, содержащую несколько слоев, будет входить порядка 5 – 10 тыс. атомов. Согласно реалистическим прогнозам, уже чуть ли не в этом году возможен переход на топологический стандарт 22 нм.
Физические законы, управляющие поведением ячеек, однако, никак не связаны с математическими законами, которые описывают процессы манипулирования информацией, представленной системой битов. В такой ситуации мы говорим о классической информации. Можно сказать и по-другому: математические законы, управляющие классической информацией, не связаны с физическими законами, описывающими поведение ячеек – носителей бита информации.
Обратим внимание на некоторые простые и совершенно очевидные черты классической информации. В данный момент времени каждый бит может иметь только одно из двух значений – либо 0, либо 1. Если у нас есть регистр, содержащий n битов, то в нем
будет записана некоторая цепочка a = (Cn-1, Cn-2 ,…, C1, C0 ), состоящая из нулей и единиц, которая представляет собой двоичную запись числа
a = C |
n-1 |
2n-1 + C |
n-2 |
2n-2 +…+ C 21 |
+ C |
20 . |
(2.1) |
|
|
1 |
0 |
|
|
Это означает, что в каждый момент времени в n-битовом классическом регистре записано только одно число. Всего же в n-битовом регистре можно записать любое из N=2n различных чисел a от 0 до 2n–1. Поэтому, как уже говорилось в книге 1, информационная емкость такого регистра, т.е. количество записанной в нем информации, есть
H = log2 N = log2 2n = n . |
(2.2) |
57 |
|
Отметим еще одну особенность классической информации. Ее можно копировать практически без всякого ущерба для самой информации. Данное свойство, как мы увидим дальше, используется для реализации так называемых обратимых вычислений. Оно также играет существенную роль в такой важной проблеме как коррекция ошибок.
Совершенно очевидно, что технологическая составляющая задачи миниатюризации элементов информационных устройств стоит на первом месте и играет ключевую роль. Нас же интересует другой аспект этой проблемы.
По-видимому, в обозримом будущем технологический прогресс приведет к тому, что вместо двух классических макроскопических состояний триггера, которые служат для идентификации двух значений бита информации, мы будем иметь дело с двумя квантовыми состояниями той или иной простой квантовой системы, т.е. окажемся в области квантовых законов манипулирования информации. В такой ситуации само понятие информации приобретает качественно новое звучание, поскольку носителем информации являются квантовые состояния, поведение которых подчиняется законам квантовой механики. Сказанное включает фактически два принципиальных положения. Во-первых, делается физическое утверждение, что информация, вообще говоря, не независима от физических законов, которые используются для ее записи и обработки. Это важное концептуальное положение высказал Рольф Ландауэр (1991 г.). Во-вторых, как отметил Антон Цайлингер в 1998 г., квантовая механика открывает такие возможности манипулирования информацией, которые принципиально отсутствуют в любых классических устройствах.
В этой главе мы поговорим о том, что входит в такое первичное понятие как квантовая информация, продолжим обсуждение основных элементов — кубитов, квантовых логических гейтов и квантовых схем, а также квантового параллелизма и других важных особенностей квантовых вычислений. Будут рассмотрены примеры физических систем, реализующих кубиты и простейшие логические гейты.
58
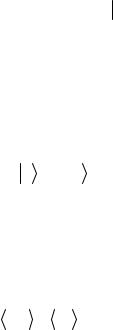
2.1. Кубиты
Рассмотрим ситуацию, когда для записи одного бита информации используются два квантовых состояния какой-либо простой квантовой системы. Такую систему называют кубитом. Это название было предложено Б. Шумахером и является сокращением вы-
ражения “квантовый бит” (по-английски qubit, т.е. quantum bit).
На первый взгляд может показаться, что такая система просто играет роль классического триггера, но только разве что существенно меньшего размера. В действительности, ситуация совершенно иная.
Речь идет о двух квантовых состояниях, которые образуют полный набор базисных состояний рассматриваемой квантовой системы. Как говорилось в главе 1, совокупность всех возможных состояний такой системы образует двумерное гильбертово пространство. Каждое квантовое состояние описывается абстрактным век-
тором, который обозначается символом … (это кэт-вектор в обо-
(это кэт-вектор в обо-
значениях Дирака). Внутри скобки пишется тот или иной значок, идентифицирующий данное квантовое состояние. Для записи информации каждому из двух базисных векторов ставится в соответствие одно из двух значений, 0 или 1, двоичной переменной. Поэтому вполне естественно использовать эти значения двоичной переменной для идентификации соответствующих базисных векторов, т.е. обозначить их как
0 и |
1 . |
(2.3) |
Таким образом, два базисных состояния (2.3) кубита соответствуют двум возможным значениям бита информации. Такой набор состояний называется вычислительным базисом. Напомним также (см. главу 1), что базисные векторы удовлетворяют условиям нормировки
0 |
|
0 = 1 |
|
1 =1, |
(2.4) |
|
|
59
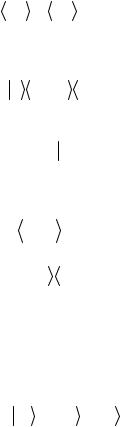
ортогональности
0 |
|
1 = 1 |
|
0 = 0 , |
(2.5) |
|
|
и полноты
0 0 |
|
+ |
|
1 1 |
|
=1. |
(2.6) |
|
|
|
Иногда бывает удобно записывать базисные векторы (2.3) в виде
C ,
,
где величина С является двоичной переменной, пробегающей значения 0 и 1. Тогда выражения (2.4) – (2.6) имеют вид
C' |
C = δCC ' , |
(2.5’) |
||||
∑ |
|
C C |
|
=1, |
(2.6’) |
|
|
|
|||||
C=0,1
где δCC’ — символ Кронекера.
Принципиальной особенностью кубита как квантового объекта является то, что он может находиться не только в одном из своих базисных состояний (2.3), но и в когерентной суперпозиции
Ψ = a |
|
0 + b |
|
1 |
(2.7) |
|
|
базисных состояний с произвольными комплексными коэффициентами a и b. Физическая интерпретация суперпозиционного состояния (2.7) состоит в том, что если в этом состоянии произвести измерение в вычислительном базисе (2.3), то с вероятностью
w = |
|
a |
|
2 |
(2.8) |
|
|
||||
0 |
|
|
|
|
|
60
