
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
Можно умножить первое уравнение слева на h, а второе на x, а затем взять их разность. В результате,
′ ′ |
(1.65) |
(ξη−ηξ) ξ η = 0 |
для каждого совместного собственного состояния. Вспомним теперь, что собственные состояния наблюдаемой должны образовывать полный набор. Отсюда следует, что совместные собственные состояния двух наблюдаемых также должны образовывать полный набор. Следовательно, из уравнения (1.65) вытекает, что
(ξη−ηξ) |
|
A = |
|
0 , |
(1.66) |
|
|
где A — произвольный кэт-вектор. Это может быть достигнуто
— произвольный кэт-вектор. Это может быть достигнуто
единственным образом, если |
|
ξη = ηξ. |
(1.67) |
Таким образом, условие одновременной измеримости двух наблюдаемых ξ и η состоит в том, что они должны коммутировать.
1.14. Соотношение неопределенностей
Как мы видели, если ξ и η — две некоммутирующие наблюдаемые, то определение значения x оставляет неопределенным значение η, и наоборот. Оказывается, можно количественно описать эту неопределенность. Для произвольной наблюдаемой ξ можно определить эрмитов оператор
Δξ = ξ− ξ , |
(1.68) |
где среднее значение берется по рассматриваемому конкретному физическому состоянию. Очевидно, что среднее значение Δξ равно нулю. Среднее значение квадрата отклонения (Δξ)2 ≡ Δξ Δξ называется дисперсией ξ и в общем случае не равно нулю. На самом деле, легко показывается, что
(Δξ)2 = ξ2 − ξ 2 . |
(1.69) |
Дисперсия ξ есть мера неопределенности значения ξ для конкретного обсуждаемого состояния (т. е. мера ширины распределения вероятных значений ξ относительно среднего значения). Если дис-
41
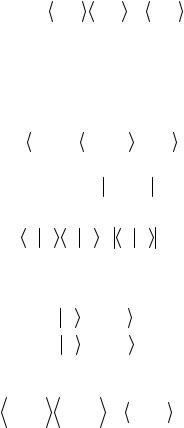
персия равна нулю, то неопределенность отсутствует и измерение ξ вынужденным образом дает среднее значение 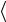 ξ
ξ .
.
Рассмотрим неравенство Шварца
A |
|
A B |
|
|
|
B ≥ |
|
A |
|
B |
|
2 , |
(1.70) |
|||||||||
|
|
|
|
|
||||||||||||||||||
аналогичное неравенству |
|
|||||||||||||||||||||
|
|
|
a |
|
2 |
|
b |
|
2 ≥ |
|
a b |
|
2 |
(1.71) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
в евклидовом пространстве. Это неравенство можно доказать, заметив, что
( A |
|
+c * B |
|
)( |
|
A +c |
|
B )≥ 0, |
(1.72) |
|
|
|
|
где с — произвольное комплексное число. Если это число принимает специальное значение −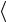 B A
B A /
/ 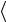 B B
B B , то предыдущее неравенство сводится к
, то предыдущее неравенство сводится к
A A B B − A B 2 ≥ 0, |
(1.73) |
что совпадает с неравенством Шварца. Подставим в неравенство Шварца
A |
= Δξ |
|
, |
(1.74) |
||
|
||||||
B |
= Δη |
|
|
, |
(1.75) |
|
|
||||||
где пустой кэт-вектор обозначает любой произвольный кэт-вектор. Находим:
(Δξ)2 (Δη)2 ≥ |
|
ΔξΔη |
|
2 , |
(1.76) |
|
|
где использовано то, что Δξ и Δη — эрмитовы операторы. Заметим далее, что
2 |
[ |
] |
2 { |
} |
|
||
ΔξΔη = |
1 |
|
Δξ, Δη + |
1 |
|
Δξ, Δη , |
(1.77) |
|
|
|
|
||||
где коммутатор [Δξ,Δη] и антикоммутатор {Δξ,Δη} определены формулами
[Δξ, Δη]≡ ΔξΔη−ΔηΔξ, |
(1.78) |
42 |
|

{Δξ, Δη} ≡ ΔξΔη+ ΔηΔξ. |
(1.79) |
Очевидно, что коммутатор антиэрмитов, т. е.
([ |
Δξ, Δη |
]) |
†= |
( |
) |
†=ΔηΔξ−ΔξΔη = − |
[ |
] |
|
|
|
ΔξΔη−ΔηΔξ |
|
Δξ, Δη , (1.80) |
в то время, как антикоммутатор, очевидно, эрмитов. Теперь легко показать, что среднее значение эрмитового оператора есть действительное число, а среднее значение антиэрмитового оператора есть чисто мнимое число. Очевидно, что правая часть равенства
ΔξΔη = |
1 |
[Δξ, Δη] + |
1 |
{Δξ, Δη} |
(1.81) |
2 |
2 |
представляет сумму чисто действительного и чисто мнимого чисел. Вычисляя квадрат модуля обеих сторон равенства, получаем:
|
|
4 |
|
[ |
] |
|
4 |
|
{ |
} |
|
||
ΔξΔη |
2 |
= |
1 |
|
|
Δξ, Δη |
2 |
+ |
1 |
|
|
Δξ, Δη |
2 , (1.82) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где использованы равенства 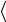 Δξ
Δξ = 0 и т. д. Последнее слагаемое в
= 0 и т. д. Последнее слагаемое в
выражении (1.82) положительно определено, так что можно написать
(Δξ)2 (Δη)2 ≥ |
1 |
|
[ξ,η] |
|
2 , |
(1.83) |
|
|
|
||||||
4 |
|||||||
|
|
|
|
|
|
где использовано соотношение (1.76). Приведенное выражение называется соотношением неопределенностей. Согласно этому соотношению, точное знание значения ξ предполагает отсутствие какого-либо знания о значении η, и наоборот. Единственным исключением из этого правила является случай, когда ξ и η коммутируют, так что в этом случае точное знание ξ не обязательно подразумевает отсутствие знания η.
1.15. Непрерывный спектр
До сих пор мы избегали иметь дело с наблюдаемыми, обладающими собственными значениями, лежащими в непрерывной области. Причина этого состоит в том, что непрерывные собственные значения требуют кэт-пространств несчетной бесконечной размер-
43

ности. К сожалению, непрерывные собственные значения в квантовой механике неизбежны. На самом деле, самые важные наблюдаемые, координата и импульс, в общем случае имеют непрерывные собственные значения. К счастью, многие результаты, полученные выше для кэт-пространства конечной размерности с дискретными собственными значениями, могут быть обобщены на кэтпространства несчетных бесконечных размерностей.
Предположим, что ξ — наблюдаемая с непрерывными собственными значениями. Уравнение на собственные значения может быть записано, как и раньше, в виде
ξ |
|
′ |
′ |
|
ξ |
′ |
. |
(1.84) |
|
|
|||||||
|
ξ |
= ξ |
|
|
Однако ξ′ могут теперь иметь значения, лежащие в непрерывной области. Для простоты предположим, что ξ′ может принимать любое значение. Условие ортогональности (1.50) обобщается до условия
′ |
|
′′ |
′ ′′ |
(1.85) |
|
||||
ξ |
|
ξ |
= δ(ξ −ξ ), |
где δ(x) обозначает дельта-функцию Дирака. Заметим, что в этом случае имеется несчетное бесконечное количество взаимно ортогональных собственных состояний ξ. Отсюда размерность кэтпространства несчетно бесконечна. Заметим также, что собственные состояния, соответствующие непрерывному спектру собственных значений, не могут быть нормированы так, чтобы их норма равнялась единице. На самом деле, все эти состояния имеют инфинитную норму, т. е. их длина бесконечна. В этом — главное отличие между собственными состояниями в конечномерном и бесконечномерном кэт-пространстве.
Необычайно полезное соотношение (1.54) обобщается следующим образом:
∫dξ |
|
ξ′ ξ′ |
|
=1. |
(1.86) |
|
|
||||
|
|
|
Заметим, что суммирование по дискретным собственным значениям заменяется интегрирование по непрерывной области собственных значения. Если ξ — наблюдаемая, то собственные состояния
44

ξ′ должны образовывать полный набор. Отсюда следует, что любой произвольный кэт-вектор может быть разложен по ξ′
должны образовывать полный набор. Отсюда следует, что любой произвольный кэт-вектор может быть разложен по ξ′ . Разложения (1.51) – (1.53) обобщаются следующим образом:
. Разложения (1.51) – (1.53) обобщаются следующим образом:
|
|
A |
= ∫dξ′ |
|
ξ′ |
|
ξ′ |
|
A , |
|
|
|
|
|
|
|
(1.87) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
A |
|
|
= ∫dξ′ |
|
A |
|
ξ′ |
|
|
ξ′ |
|
, |
|
|
|
|
|
|
2 |
(1.88) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
A |
|
′ |
A |
|
′ |
|
′ |
|
A |
= ∫dξ |
′ |
|
A |
|
′ |
|
=1. (1.89) |
||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
A = ∫dξ |
|
ξ |
ξ |
|
|
|
|
ξ |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эти результаты также просто следуют из (1.86). Заметим, что из (1.89) следует обобщенное условие нормировки состояний
A |
|
′ |
|
A |
|
′ |
|
2 |
=1. |
(1.90) |
|
|
|
|
|||||||
|
|
|||||||||
|
A = ∫dξ |
|
|
ξ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1.16. Чистые и смешанные состояния. Матрица плотности
Вернемся к понятию квантового состояния физической системы, с которого начинается построение аппарата квантовой механики. Физическое содержание и конкретная математическая форма этого вводимого a priori понятия подразумевает, что сформулировано некоторое описание (или, используя терминологию работы Эрвина Шрёдингера 1935 г., представлен к рассмотрению каталог), которое включает информацию о результатах всех возможных измерений, производимых над этой системой.
До сих пор мы говорили о том, что состояние замкнутой квантовой системы может быть описано кэт-вектором ψ . Такое состоя-
. Такое состоя-
ние называется чистым состоянием. Коснемся некоторых специфических особенностей чистых состояний. Прежде всего, сам век-
тор ψ данного чистого состояния можно рассматривать как один
данного чистого состояния можно рассматривать как один
из собственных векторов некоторого полного набора наблюдаемых, т. е. он входит в некоторый полный набор базисных состояний. В каждом из базисных состояний и, следовательно, в состоя-
нии ψ наблюдаемые указанного полного набора имеют определенные значения. Это означает, что для чистого состояния сущест-
наблюдаемые указанного полного набора имеют определенные значения. Это означает, что для чистого состояния сущест-
45

вует полная совокупность измерительных процессов, которые приводят с достоверностью к определенным результатам. Поскольку процесс измерения, согласно постулату фон Неймана, представляет собой проектирование на базисные состояния, мы говорим, что чистое состояние возникает в результате полного набора измерений, т. е. в результате полного опыта.
Описание с помощью кэт-вектора ψ является наиболее полным возможным в квантовой механике описанием квантового состояния. Знание ψ
является наиболее полным возможным в квантовой механике описанием квантового состояния. Знание ψ позволяет предсказывать, каков может быть
позволяет предсказывать, каков может быть
результат того или иного измерения, производимого над системой, и какова вероятность получения этого результата. Поскольку квантовое измерение обычно разрушает состояние, то вероятность реализуется в ансамбле измерений, производимых над одинаковыми системами, которые приготовлены в одном и том же состоянии
ψ .
.
Существуют, однако, квантовые состояния более общего вида, которые нельзя описать с помощью кэт-векторов. Другими словами, есть состояния, описание которых не обладает той максимальной степенью полноты, которая присуща чистым состояниям. Такие состояния называются смешанными, а для их описания используется формализм матрицы плотности, введенный в квантовую механику в 1927 г. Львом Ландау и Иоганном фон Нейманом.
Сам факт существования смешанных состояний легко понять, если рассмотреть квантовую систему, состоящую из двух подсистем А и В. Для простоты эти подсистемы можно считать невзаимодействующими друг с другом. Пространством состояний всей системы является прямое произведение НА НВ гильбертовых про-
странств НА и НВ подсистем А и В. Пусть { n A}и {ν
A}и {ν B}есть пол-
B}есть пол-
ные ортонормированные наборы состояний1 этих подсистем в пространстве, соответственно, НА и НВ. Если взять прямые произведе-
ния n A ν
A ν B ≡ n
B ≡ n
 ν
ν , то их совокупность { n
, то их совокупность { n
 ν
ν } образует пол-
} образует пол-
1 Для удобства базисные кэт-векторы подсистемы А мы будем идентифицировать с помощью латинских букв, а подсистемы В — с помощью греческих. Это позволит, в частности, опускать далее значки А и В.
46

ный набор состояний составной системы. Каждое из состояний имеет факторизованный вид, т. е. представляет собой произведение кэт-векторов, относящихся к подсистемам А и В. Это означа-
ет, что каждая из подсистем находится в чистом состоянии, заданном своим кэт-вектором.
В соответствии с принципом суперпозиции произвольное чистое квантовое состояние ψAB  полной системы задается кэтвектором
полной системы задается кэтвектором
ψAB = ∑ cnν |
|
n |
|
ν , |
(1.91) |
|
|
||||
n,ν |
|
|
|
|
|
удовлетворяющим условию нормировки
ψ |
AB |
|
ψ |
AB |
= ∑ |
|
c |
|
2 |
=1. |
(1.92) |
|
|
|
|||||||||
|
|
|
n,ν |
|
nν |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Физический смысл коэффициентов разложения сnν состоит в том, что величина | сnν|2 дает вероятность обнаружить подсистему А в
состоянии n и одновременно подсистему В в состоянии ν
и одновременно подсистему В в состоянии ν . Та-
. Та-
ким образом, каждое конкретное состояние подсистемы А скоррелировано с каким-то состоянием подсистемы В.
Теперь обратим внимание, что коэффициенты сnν не могут быть, вообще говоря, представлены в виде произведения каких-то коэффициентов Аn и Bν, т. е. в общем случае сnν ≠ АnBν. Это означает,
что кэт-вектор ψAB  , вообще говоря, не может быть представлен в виде произведения кэт-векторов ϕA
, вообще говоря, не может быть представлен в виде произведения кэт-векторов ϕA и χB
и χB  , которые описывали бы независимым и полным образом чистые квантовые состояния подсистем, ψAB
, которые описывали бы независимым и полным образом чистые квантовые состояния подсистем, ψAB ≠ ϕA
≠ ϕA
 χB
χB  . Поэтому описание квантового
. Поэтому описание квантового
состояния одной из подсистем (например, А или В) будет характеризоваться меньшей степенью полноты, чем в случае чистого состояния.
Отметим следующую особенность рассмотренной нами ситуации. Вся система находится в чистом состоянии, и ее описание с помощью кэт-вектора является максимально полным. При этом описание каждой из подсистем, как мы видим, может не быть максимально полным. В этом суть отмеченного Э. Шрёдингером важ-
47
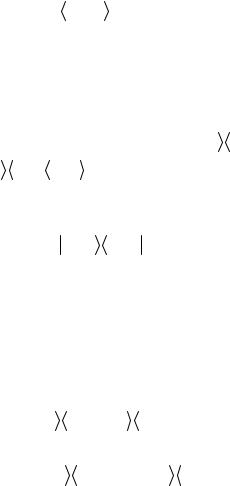
ного квантового свойства, что полное знание о состоянии всей системы не соответствует такому же полному знанию о состоянии ее частей.
В дальнейшем нам понадобится такая величина как след опера-
тора. По определению, следом оператора ˆ называется сумма его
F
диагональных матричных элементов, вычисленных в каком-то базисе:
ˆ |
j |
|
ˆ |
|
j . |
(1.93) |
|
|
|||||
SpF ≡ ∑ |
|
F |
|
|||
j |
|
|
|
|
|
|
Укажем несколько полезных свойств величины ˆ :
SpF
1.След оператора не зависит от выбора базисных состояний.
2.Циклическая перестановка операторов, произведение которых стоит под знаком Sp, не меняет величину следа.
3. Если |
|
|
|
|
|
|
ˆ |
|
ψ ψ |
|
, то |
|
|
||||||||||
оператор имеет вид F = |
|
|
|||||||||
ˆ |
= Sp |
|
ψ ψ |
|
= ψ |
|
ψ . |
||||
|
|
|
|||||||||
SpF |
|
|
|
||||||||
Для описания состояния подсистемы А вводится оператор плот-
ности |
), |
|
ρˆ A = SpB ( ψAB ψAB |
(1.94) |
где символ SpB(…) обозначает операцию взятия следа по квантовым числам подсистемы В от оператора, стоящего в круглых скобках. Во избежание недоразумений обратим внимание, что вычисление следа в выражении (1.94) производится только по состояни-
ям подсистемы В. Поэтому величина ρˆ A представляет собой ли-
нейный оператор, действующий в гильбертовом пространстве НА состояний подсистемы А. Подставляя разложение (1.91) в (1.94), получаем:
ρˆ |
A |
= |
∑ |
c c |
|
n m |
|
Sp |
B |
|
ν μ |
|
= |
|
|
|||||
|
|
|
|
|||||||||||||||||
|
|
|
nν mμ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
nν, mμ |
|
|
|
|
|
|
|
|
(1.95) |
||||||||
|
|
|
|
∑cnνcmv |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
n m |
|
≡ ∑ ρnm |
|
n m |
|
. |
||||||||||
|
|
= ∑ |
|
|
|
|
|
|||||||||||||
|
|
|
nm |
ν |
|
|
48 |
|
|
nm |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

При вычислении мы воспользовались тем, что операция взятия
следа относительно подсистемы В дает |
SpB |
|
ν |
μ |
|
= μ |
|
ν = δμν. |
|||||||
|
|
|
|||||||||||||
Совокупность величин |
|
|
|
|
|
|
c |
|
|
|
|
|
|||
(ρˆ |
A |
) |
nm |
≡ ρ |
nm |
≡ ∑c |
|
(1.96) |
|||||||
|
|
|
nν |
mν |
|
|
|
|
|
||||||
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
образует матрицу оператора ρˆ A в базисе состояний { n }.
}.
Перечислим основные свойства оператора плотности.
1. Из выражений (1.95) и (1.96) следует, что ρˆ A есть эрми-
товый оператор, т. е.
ρˆ A = ρˆ +A .
2. Из эрмитовости ρˆ A следует, что в НА существует такой полный ортонормирванный базис { i } , в котором оператор ρˆ A
} , в котором оператор ρˆ A
диагонализуется, т. е. может быть записан в виде спектрального разложения
ρˆ |
A |
= ∑ p |
|
i i |
|
, |
(1.97) |
|
|
||||||
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
где pi — действительные собственные значения ρˆ A .
3. Используя этот базис в разложении (1.95), получаем, что
p |
= ρ |
= ∑c |
c |
= ∑ |
|
c |
|
2 |
≥ 0, |
(1.98) |
|
|
|||||||||
i |
ii |
iν |
iν |
|
|
iν |
|
|
|
|
|
|
ν |
|
ν |
|
|
|
|
|
|
т. е. собственные значения оператора ρˆ A неотрицательны. Такой оператор называется неотрицательно определенным оператором.
4. Sp |
A |
ρˆ |
A |
= ∑ |
|
c |
|
2 = ∑ p |
=1, т. е. 0 ≤ p ≤1. |
(1.99) |
|
|
|||||||||
|
|
|
|
nν |
|
i |
i |
|
||
|
|
|
|
n |
|
|
|
i |
|
|
5. Матрица плотности ρˆ A позволяет вычислить вероят-
ность получения того или иного результата измерения любой физической величины (наблюдаемой), относящейся к подсистеме А.
Действительно, пусть ˆA есть оператор такой величины.
F
49
Тогда, например, для среднего значения |
ˆ |
|
|
|
в состоянии (1.89) |
|||||||||||||||
FA |
|
|||||||||||||||||||
получаем: |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
FA = ψAB |
|
|
ψAB |
= |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
FA |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m |
|
ˆ |
|
n |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= ∑ cnνcmν |
|
FA |
|
|
|
|
|
|
||||||||||
|
|
nmν |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
(ρˆ |
|
|
|
ˆ |
(1.100) |
|
|
= ∑ ρ |
|
|
) |
|
|
|
= Sp |
|
|
|
|
). |
||||||
|
|
nm |
(F |
mn |
A |
A |
F |
|||||||||||||
|
|
nm |
A |
|
|
|
|
|
|
A |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
F есть собственное |
состояний |
|
|
|
|
ˆ |
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
оператора FA , отве- |
||||||||||||||||||
чающее собственному значению F. Чтобы найти вероятность получения результата F при измерении данной физической величины в состоянии (1.91), нужно вычислить среднее значение проекционно-
ˆ |
|
F |
F |
|
, т. е. вычислить |
||
|
|
||||||
го оператора PF = |
|
|
|||||
WF = |
ˆ |
= SpF (ρˆ |
ˆ |
||||
PF |
APF ). |
||||||
Используя спектральное разложение (1.97), получаем
WF = SpA (ρˆ |
ˆ |
|
F |
|
i |
|
2 |
. |
|
|
|
||||||
APF )= ∑ pi |
|
|
|
|
||||
|
i |
|
|
|
|
|
|
|
(1.101)
(1.102)
Выражение (1.102) допускает прозрачную физическую интер-
претацию. Величина WF(i) = 
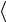 F i
F i
 2 есть вероятность того, что при
2 есть вероятность того, что при
измерении величины F в состоянии i мы обнаружим указанное
мы обнаружим указанное
собственное значение F. Что же касается величин рi, то согласно (1.97), они имеют смысл вероятности обнаружить чистое состояние
i в смешанном состоянии подсистемы А, которое описывается с помощью матрицы плотности ρˆ A . Поэтому вероятность получения результата F при измерении в состоянии с матрицей плотности ρˆ A строится стандартным образом как произведение указанных
в смешанном состоянии подсистемы А, которое описывается с помощью матрицы плотности ρˆ A . Поэтому вероятность получения результата F при измерении в состоянии с матрицей плотности ρˆ A строится стандартным образом как произведение указанных
вероятностей WF(i) и рi, просуммированное по всем состояниям i:
WF = ∑ piWF(i). Итак, матрица плотности полностью отвечает тем i
50
